Теория пределов
Определение предела функции в точке
Сформулируем определение предела функции в точке.
Определение. Пусть функция f(x) определена в некоторой окрестности точки а, кроме, может быть, самой точки а, Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хп ¹ а, п Î N, сходящейся к а, последовательность соответствующих значений функции f(xп), п Î N, сходится к числу В.
В этом случае пишут: 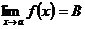 или
или 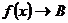 при
при 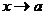 .
.
Если же для некоторой последовательности значений аргумента, сходящейся к а, соответствующая последовательность значений функции не является сходящейся, то функция в данной точке не имеет предела. То же заключение можно сделать, если для двух различных последовательностей значений аргумента последовательности соответствующих значений функции имеют различные пределы.
Очевидно, число В является пределом функции 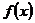 при
при 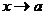 тогда и только тогда, когда
тогда и только тогда, когда 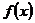 можно представить в виде:
можно представить в виде:
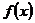 = В +
= В + 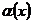 , где
, где 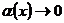 при
при 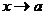 .
.
Отметим, что точка а, в которой рассматривается предел функции 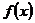 , может принадлежать области определения функции
, может принадлежать области определения функции 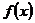 , а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
, а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
Свойства пределов функций
Основные свойства пределов функций аналогичны теоремам о пределах числовых последовательностей:
1) Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: 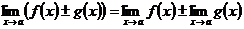 .
.
2) Предел произведения функций равен произведению их пределов, если последние существуют: 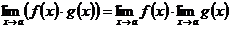 .
.
Следствие. Постоянный множитель можно выносить за знак предела: 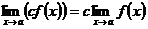 , если
, если 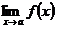 существует.
существует.
3) Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: 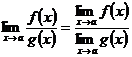 , если
, если 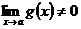 .
.
При изучении пределов функций иногда полезно использовать следующую «теорему о пределе промежуточной функции».
Теорема. Если 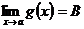 ,
, 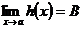 и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства
и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства 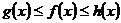 , то
, то 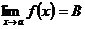 .
.
 2017-11-30
2017-11-30 337
337








