Производная сложной функции
Определение производной
Рассмотрим функцию  , где
, где  (рис. 31). Возьмем произвольную точку
(рис. 31). Возьмем произвольную точку  . Для любого
. Для любого  разность х – х 0 называется приращением аргумента х в точке х 0 и обозначается
разность х – х 0 называется приращением аргумента х в точке х 0 и обозначается  . Таким образом,
. Таким образом,

Разность  называется приращением функции в точке х 0.
называется приращением функции в точке х 0.
Производной функции 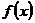 в точке х0 называется предел отношения приращения функции
в точке х0 называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при
при  , если этот предел существует и обозначается
, если этот предел существует и обозначается 

Функция, имеющая производную в точке х 0, называется дифференцируемой в этой точке. Если же функция дифференцируема в каждой точке некоторого интервала  , то она дифференцируема на этом интервале. Необходимое условие существования производной вытекает из следующей теоремы.
, то она дифференцируема на этом интервале. Необходимое условие существования производной вытекает из следующей теоремы.
Теорема. Если функция 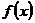 дифференцируема в точке х0, то она непрерывна в этой точке.
дифференцируема в точке х0, то она непрерывна в этой точке.
Однако непрерывность функции в точке не является достаточным условием дифференцируемости функции в точке.
 2017-11-30
2017-11-30 263
263








