Исходные данные к РГР № 5

 

Первая цифра шифра	m, т	β	Вторая цифра шифра		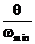α	F 1, кН	F 2, кН	Третья цифра шифра (№схемы)	l, м	h, м	EI 1, кН·м2
	0,5			0,5	1,5
	0,6	1,5		0,55
	0,7			0,6	2,5
	0,8	2,5		0,65
	0,9			0,7	1,5
	1,0			0,68
	1,1	1,5		0,8	2,5
	1,2			0,72
	1,3	2,5		0,66	3,5
	1,4			0,58

 

Примечание. Втаблицеприведеныамплитудныезначениявибрационнойнагрузки F_i (t)= F_i sinθ t.

 

Последовательностьрасчета

 

5.1.Вычертитьвмасштабезаданнуюрасчетнуюсхемурамысуказаниемразмеров,величинмасс,вибрационнойнагрузкиисоотношенияжесткостейстержней.

5.2.Определитьчислостепенейсвободысосредоточенныхмассзаданнойрасчетнойсхемы.

 

Рис.5.1.СхемызаданийкРГР№5

5.3.Показатьрасчетнуюсхемурамыпридействииамплитудныхзначенийинерционныхсиливибрационнойнагрузки.

5.4.Записатьвобщемвидеуравнениечастотсвободныхколебанийприменительнокзаданнойрасчетнойсхеме.

5.5.Понаправлениювозможныхсмещениймасспоследовательноприложитьединичныесилыиотдействиякаждойизнихпостроитьэпюрыизгибающихмоментов M_i.

5.6.Определитькоэффициентыуравнениячастот

,

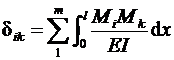где m –числоучастковинтегрирования.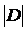

5.7.Составитьуравнениечастотвчисленномвиде.

5.8.Определитькорничастотногоуравненияl _i (i =1… n)ипроизвестипроверкиправильностиегорешения:

,

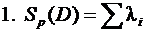где S_p (D)–след(суммаглавныхкоэффициентов)матрицы,составленной из коэффициентов частотного уравнения; 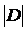– величина определителя этой матрицы

5.9.Определитьчастотыипериодысвободныхколебаниймасс.

5.10.Вычислитьотносительныеамплитудымассипостроитьформыколебанийдлякаждойчастоты.

5.11.Изопределенноговп.5.7спектрачастотсвободныхколебанийвыявитьнаименьшеезначениеω_minиопределитькруговуючастотувынужденныхколебанийпозаданномувтабл.5.1соотношению.

5.12.Показатьрасчетнуюсхемурамыпридействиинанееамплитудныхзначенийнагрузокиинерционныхсил.

5.13.Записатьвобщемвидесистемуканоническихуравненийдляопределенияамплитудныхзначенийинерционныхсилприменительнокзаданнойрасчетнойсхеме.

5.14.Построитьвзаданнойрасчетнойсхемеэпюруизгибающихмоментов M_F отдействияамплитудныхзначенийвибрационной нагрузки.

5.15.Определитьглавныекоэффициентысистемыканоническихуравнений

.

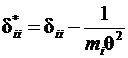Побочныекоэффициентысистемыканоническихуравненийимеюттежезначения,чтоивуравнениичастот.

5.16.Определитьсвободныечленысистемыканоническихуравнений

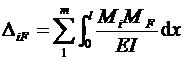
5.17.Записатьсистемуканоническихуравненийвчисленномвидеиизеерешенияопределитьамплитудныезначенияинерционныхсил J_i.

5.18.Построитьдинамическуюэпюруизгибающихмоментов

M _дин= M ₁ J ₁+ M ₂ J ₂+…+ M_nJ_n + M_F.

5.19.Определитьамплитудымасс a_i = J_i/m_i ∙θ²ипостроитьдеформированнуюсхемурамыпривынужденныхколебаниях.