Пусть векторы  и
и 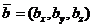 заданы своими проекциями на оси координат
заданы своими проекциями на оси координат  или, что то же самое
или, что то же самое
 .
.
Линейные операции над векторами:
-
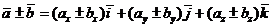 ,
,
или 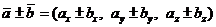 .
.
-
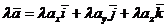 , или
, или 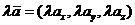 .
.
Равенство векторов:
Два вектора  и
и 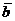 равны тогда и только тогда, когда выполняются равенства
равны тогда и только тогда, когда выполняются равенства 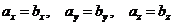 , т.е.
, т.е.
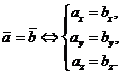
Коллинеарность векторов:
Так как 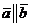 , то можно записать
, то можно записать 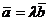 , где
, где 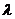 - некоторое число. То есть
- некоторое число. То есть 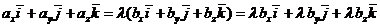 .
.
Отсюда
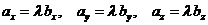 ,
,
т.е. 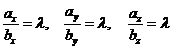 , или
, или 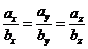 .
.
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.
Координаты точки:

Пусть в пространстве задана прямоугольная декартова система координат  . Для любой точки
. Для любой точки  координаты вектора
координаты вектора  называются координатами точки
называются координатами точки  . Вектор
. Вектор  называется радиус-вектором точки
называется радиус-вектором точки  , обозначается
, обозначается 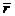 ,
, 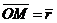 .
.
Следовательно, координаты точки – это координаты ее радиус-вектора 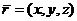 или
или 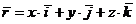 .
.
Координаты точки  записываются в виде
записываются в виде 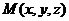 .
.
Координаты вектора:
Найдем координаты вектора 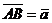 . Пусть
. Пусть 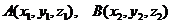 .
.

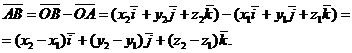
Итак, 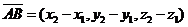 .
.
 2017-11-30
2017-11-30 662
662







