Векторы. Основные определения
Определение. Вектор – это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление.
Если  - начало вектора, а
- начало вектора, а  - его конец, то вектор обозначается символом
- его конец, то вектор обозначается символом  (или
(или  ).
).
Вектор  (у него начало в точке
(у него начало в точке  , а конец в точке
, а конец в точке  ) называется противоположным вектору
) называется противоположным вектору  . Вектор, противоположный вектору
. Вектор, противоположный вектору  , обозначается
, обозначается  .
.
Длиной или модулем вектора  называется длина отрезка, обозначается
называется длина отрезка, обозначается  . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  .
.
Вектор, длина которого равна единице, называется единичным вектором и обозначается  .
.
Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора
, называется ортом вектора  и обозначается
и обозначается  .
.
Определение. Векторы  и
и 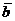 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают  .
.
Нулевой вектор коллинеарен любому вектору.
Два вектора  и
и 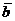 называются равными (
называются равными ( ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Определение. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или параллельных плоскостях.
Линейные операции над векторами
Пусть  и
и 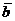 - два произвольных вектора. Возьмем произвольную точку
- два произвольных вектора. Возьмем произвольную точку  и построим вектор
и построим вектор  . От точки
. От точки  отложим вектор
отложим вектор  . Вектор
. Вектор  , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  и
и 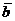 :
:  .
.

Это правило сложения векторов называют правилом треугольника.
Сумму двух векторов можно находить также по правилу параллелограмма.

Под разностью векторов  и
и 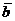 понимается вектор
понимается вектор  такой, что
такой, что  .
.

В параллелограмме, построенном на векторах  и
и 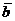 , одна направленная диагональ является суммой векторов
, одна направленная диагональ является суммой векторов  и
и 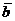 , а другая – разностью.
, а другая – разностью.

Произведением вектора  на число
на число 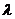 называется вектор
называется вектор  , который имеет длину
, который имеет длину  , коллинеарен вектору
, коллинеарен вектору  , имеет направление вектора
, имеет направление вектора  , если
, если 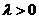 и противоположное направление, если
и противоположное направление, если 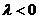 .
.

Из определения следует, что  , т.е. каждый вектор равен произведению его модуля на орт.
, т.е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
|
|
 2017-11-30
2017-11-30 701
701
 ,
,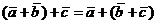 ,
, ,
, ,
, .
.






