2017-11-30
893
1) Находим область допустимых решений (ОДР). Для этого строим граничные прямые и определяем полуплоскости, координаты точек которых удовлетворяют неравенствам-ограничениям.
Рассмотрим первое ограничение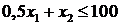 
. Строим прямую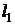 
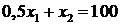как прямую в отрезках по двум точкам: 
, 
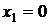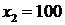и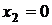 
, 
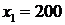. Берём произвольную точку, не лежащую на этой прямой, например О(0,0). Подставляем её координаты в первое ограничение. Если неравенство в этой точке выполняется, то первое ограничение определяет полуплоскость, которая содержит выбранную точку, если нет, то оно определяет полуплоскость, в которой не лежит выбранная точка. В точке О(0,0) неравенство выполняется следующим образом: 
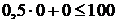. Поэтому первое ограничение определяет полуплоскость, расположенную ниже прямой 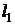. На рис. 2.2.1 это отмечено двумя стрелками.
Рассмотрим второе ограничение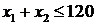 
. Строим прямую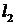 
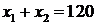как прямую в отрезках по двум точкам: , 
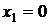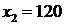и ,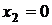 
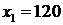. Берём произвольную точку, не лежащую на этой прямой, например О(0,0). Подставляем её координаты во второе ограничение. В точке О(0,0) неравенство выполняется следующим образом: 
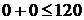. Поэтому второе ограничение определяет полуплоскость, расположенную ниже прямой 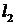. На рис. 2.2.1 это отмечено двумя стрелками.
|
|
|
Рассмотрим третье ограничение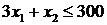 
. Строим прямую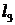 
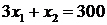по двум точкам: , 
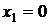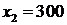и ,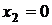 
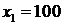. Берём произвольную точку, не лежащую на этой прямой, например О(0,0). Подставляем её координаты в третье ограничение. В точке О(0,0) неравенство выполняется следующим образом: 
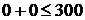. Поэтому третье ограничение определяет полуплоскость, расположенную ниже прямой 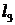. На рис. 2.2.1 это отмечено двумя стрелками.
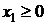определяет правую полуплоскость относительно оси 0 х 2,
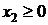определяет верхнюю полуплоскость относительно оси 0 х 1.
Из условий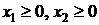 
следует, что ОДР находится в первой четверти.
Выделяем ОДР 
пятиугольникO ABCD.
2) Строим вектор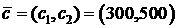 
или вектор ему коллинеарный – направление наибольшего возрастания функции Z
.
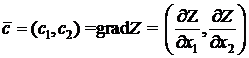3) Строим прямую ^ вектору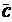 
, желательно, чтобы она пересекала ОДР. Можно строить прямую 
.
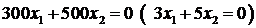4) Перемещаем эту прямую в направлении вектора 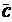, пока она станет опорной к ОДР. Опорной прямой выпуклого многоугольника называется прямая, которая имеет хотя бы одну общую точку с этим многоугольником и он расположен по одну сторону от нее. Перемещаемая прямая становится опорной в точке B.
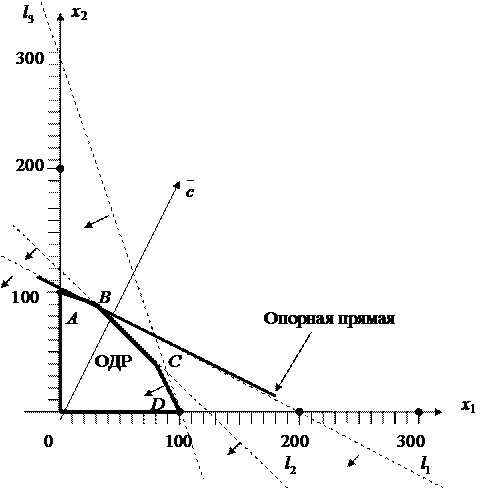
Рис. 2.2.1. Графическое решение задачи 2.2.1
5) Находим координаты точки B: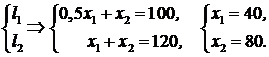 
6) Находим значение целевой функции в точке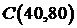 
:
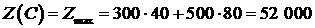
Ответ. Фирма для получения максимальной прибыли 52 000 грн. должна изготовить 40 деталей первого вида и 80 деталей – второго.
