2017-11-30
3269
2.1.Составление математических моделей задач линейного программирования
2.1.1. Задача об оптимальном плане выпуска продукции. Найти оптимальное распределение пашни под посев трёх культур: капусты, картофеля и люпина при условии, что в хозяйстве имеется 720 га пашни, 9 тыс.тонн органических удобрений, количество чел./дней труда составляет 50 тыс.
Затраты ресурсов и выход валовой продукции в денежном выражении в расчёте на 1га указанных культур приведены в табл.1.1.
Таблица 2.1. Исходные данные задачи 2.1.1
| Показатель | Культура | ||
| Капуста | Картофель | Люпин | |
| Затраты органических удобрений, т | |||
| Затраты труда, чел./ дней | |||
| Выход валовой продукции, грн./ га | 20 000 | 18 000 | 8 000 |
Требуется определить посевов культур, максимизирующий валовую продукцию в денежном выражении при условии, что площадь, занимаемая люпином, должна быть не менее 100 га.
Решение. Математическая модель задачи линейного программирования (ЗЛП) составляется путем экономического анализа по следующей схеме:
|
|
|
1) вводят переменные;
2) формируют целевую функцию;
3) формируют ограничения;
4) налагают условия неотрицательности переменных (или указывают интервалы изменения переменных).
Ограничимся составлением математической модели задачи. Обозначим через 
количество гектаров пашни, отведенное под каждую культуру соответственно.
Целевая функция 
это выражение, которое необходимо максимизировать или минимизировать. В нашем случае это общий выход валовой продукции в денежном выражении. Валовая продукция капусты в денежном выражении равна 
грн., картофеля 
грн., люпина 
грн. Поэтому 
.
На один гектар под капусту вносится 15 т органических удобрений, поэтому на 
га будет внесено 
т, соответственно под картофель надо внести 
т и под люпин 
т. Общее количество органических удобрений не превышает 9 тыс. т. Имеем первое ограничение 
Аналогично по трудовым ресурсам получаем второе ограничение 
. Сумма площадей, отведённых под культуру, не превышает 729 га. Таким образом имеем третье ограничение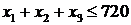 
. Так как под люпин отводится не менее 100 га, то имеем четвёртое ограничение 
По условию переменные неотрицательные, т.е. 
Объединяя полученные результаты, получаем математическую модель задачи:
Решать такие задачи следует специальными приёмами.
Довольно просто они решаются с использованием компьютера. Решение, полученное с помощью компьютера, имеет вид
, 
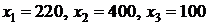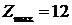млн. грн.
2.1.2. Задача о рационе. При составлении суточного рациона кормления скота можно использовать свежее сено (не более 60 кг) и силос (не более 80 кг). Рацион должен содержат не менее 35 кормовых единиц, 1 кг белка, 100 г кальция и 80 г фосфора. В таблице приведены данные о содержании указанных питательных веществ в 1кг каждого корма и себестоимость этих кормов.
|
|
|
| Корм | Компоненты | Себестоимость коп./ кг | ||||
| Количество кормовых единиц | Белок, г/кг | Кальций г/ кг | Фосфор г/ кг | |||
| Сено | 0,4 | 1,26 | ||||
| Силос | 0,6 | 2,6 | ||||
Определить оптимальный рацион исходя из минимума его себестоимости.
Решение. Обозначим через и 
соответственно количество сена и силоса, которое предполагается включить в рацион. Из условия непосредственно следуют два ограничения:
, 
.
Количество кормовых единиц, содержащихся в рационе (; ), можно выразить суммой: 
. По условию эта величина не может быть меньше 35 единиц, т. е.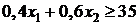 
. Ограничения по содержанию в рационе белка, кальция и фосфора примут следующий вид: 
; 
; 
. Естественно также, что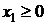 
и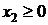 
.
В принятых обозначениях себестоимость рациона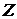 
можно выразить в виде следующей функции: 
.
Итак, задача сводится к определению таких значений: 
и 
, удовлетворяющих составленным выше ограничениям, при которых линейная функция 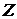достигает наименьшего значения, т. е. к решению задачи
2.1.3. Задача о раскрое материалов. Заготовки длиной 4 м надо разрезать на детали длиной 1,6 м, 1,4 м, 1 м. Первых надо получить 60 шт., вторых − 50 шт., третьих − 70 шт. Количество заготовок неограниченно. Надо найти количество заготовок, которое необходимо разрезать, чтобы было минимальное количество отходов, и при этом получить требуемое количество деталей.
Решение. Составим схему раскроя, то есть, определим способы раскроя.
| ____ 1,6 ____|____ 1,6 ____ | __ 0,8 _ | ~ х 1
|____ 1,6 ____ | ____ 1,4 ___|__ 1 ___ | ~ х 2
|____ 1,6 ____ | ___ 1 _ _|_ 1__ | 0,4 | ~ х 3
|___1,4__|___1.4__|__1 |_0,2| ~ х 4
|__1.4___|__1__|__1__| 0,6 _ | ~ х 5
|__1__|__1__|__1_ |_1_ | ~ х 6
Рис. 1.1. Способы раскроя заготовок
В данном примере существует шесть способов раскроя. Способы раскроя и соответствующие переменные желательно внести в таблицу
| Размер детали (м) | Требуемое количество деталей (шт.) | Варианты раскроя | Остаток заготовок (шт.) | |||||
| 1,6 | u 1 | |||||||
| 1,4 | u 2 | |||||||
| u 3 | ||||||||
| Остаток материала (м) | 0,8 | 0,4 | 0,2 | 0,6 | ||||
Число заготовок, которые режутся  м способом
| x 1 | x 2 | x 3 | x 4 | x 5 | x 6 |
Обозначим:
Z − количество отходов (м),
− число заготовок (в шт.), которые режутся j -м способом,
− остаток заготовок (в шт.) длиной 1,6 м, 1,4 м, 1 м соответственно. Тогда математическая модель задачи имеет вид
Замечание. Задача о раскрое часто формулируется иначе. Для нашего примера она имеет следующий вид.
Требуется получить максимальное количество комплектов деталей по 1,6 м, 1,4 м, и 1 м в соотношении 2:4:3 в каждом комплекте из имеющихся 150 заготовок.
Решение. Введём дополнительно ещё одну переменную 
количество комплектов.
Тогда математическая модель задачи примет вид:
2.1.4. Транспортная задача. В городе имеются три хлебозавода, которые снабжаются мукой четырёх мелькомбинатов. Потребности в муке хлебозаводами соответственно равны 30, 20, 40 т. Возможности мелькомбинатов соответственно равны 15, 20, 30, 25 т.
Стоимость перевозки 1 т муки от мелькомбинатов до хлебозавода показаны в таблицу:
| Мелькомбинат | Хлебозавод | Суточная производительность, т | ||
| №1 | №2 | №3 | ||
| №1 | ||||
| №2 | ||||
| №3 | ||||
| №4 | ||||
| Суточная потребность в муке, т |
Требуется организовать поставку муки хлебозаводам таким образом, чтобы полностью обеспечить их работой с минимальными транспортными расходами.
Решение. Проверяем наличие закрытости транспортной модели.
Суточная потребность в муке равна 30+20+40=90 (т), а суточная производительность 15+20+30+25=90 (т). Так как эти величины равны между собой, то модель закрыта.
|
|
|
Составим математическую модель задачи.
Введём переменные 
–количество муки, которое планируется перевозить от i -го мелькомбината к j -у хлебозаводу (например, х 21 –количество муки, которое планируется перевозить от второго мелькомбината к первому хлебозаводу), Z – суммарные транспортные издержки, которые надо минимизировать:
С первого мелькомбината вывозится 
т муки и так как задача закрыта, то эта величина равна 15 т, что записывается в виде равенства 
. Количество привезённой муки на первый хлебозавод равно 
и оно равно 30 т, т.е. 
. Поступая аналогично по остальным мелькомбинатам и хлебозаводам, получаем математическую модель задачи:
2.1.5. Задача о назначениях. Найти оптимальное направление трёх погрузчиков на погрузку трёх видов контейнеров, если известны производительности каждого погрузчика (контейнер/день) при погрузке каждого вида контейнера, которые представлены в таблице
| Контейнеры Погрузчики | |||
Каждый погрузчик может быть направлен на погрузку только одного вида контейнеров и каждый вид контейнеров может погружаться только одним видом погрузчиков в связи с необходимостью переоборудовать погрузчик под погрузку определённого вида контейнеров. Составить оптимальный план распределения погрузчиков (ограничиться составлением математической модели).
Решение. Введём переменные.
Обозначим через 
направление i -го погрузчика на погрузку j -го вида контейнеров. Считаем, что
| если i -й погрузчик направляется на погрузку j -го вида контейнеров, |
| если i -й погрузчик не направляется на погрузку j -го вида контейнеров. |
Z − общее количество погружённых контейнеров в день.
Исходные данные и xij для наглядности запишем в таблицу
| Контейнеры Погрузчики | ||||||
| х 11 | х 12 | х 13 | ||||
| х 21 | х 22 | х 23 | ||||
| х 31 | х 32 | х 33 |
Общее количество погруженных контейнеров
|
|
|
.
Из чисел xij в каждой строке и каждом столбце одно равно единице, а остальные нулю.
Поэтому математическая модель задачи имеет следующий вид:
|
| если i -й погрузчик направляется на погрузку j -го вида контейнеров, |
| если i -й погрузчик не направляется на погрузку j -го вида контейнеров. |
2.2. Решение задач линейного программирования и анализ полученного решения
Задача 2.2.1. Фима «Молот»» получила заказ на изготовление деталей двух видов из цинка, меди и олова. Запасы сырья и прибыль от реализации каждого изделия внесены в табл. 2.2.1.
Таблица 2.2.1. Исходные данные выпуска продукции задачи 2.2.1
| Сырьё | Продукция (расходы сырья на единицу продукции, кг) | Запасы сырья, кг | |
| P 1 | P 2 | ||
| Цинк | 0,5 | ||
| Медь | |||
| Олово | |||
| Цена ед. продукции | 300 грн. | 500 грн. | |
| Количество продукции, ед. | x 1 | x 2 |
Найти план выпуска продукции, чтобы доход от её реализации был максимальный.
Решить задачу: 1) графически, 2) с помощью симплекс-метода, 3) с помощью «Поиска решений» в Excel, 4) составить двойственную задачу, 5) найти решение двойственной задачи, 6) определить дефицитность ресурсов, 7) найти интервалы устойчивости по сырью и ценам, 8) проверить целесообразность выпуска третьего изделия по цене 400 грн. и затратами металла 1кг, 0,5 кг и 2,5 кг соответственно.
Решение. Обозначим через х 1 количество выпуска продукции первого вида, х 2 – второго, Z – доход от реализации всей продукции. Тогда математическая модель задачи имеет вид
