Решаем задачу с помощью Поиска решений в Excel

Методика решения задачи симплекс-методом с
использованием Microsoft Excel

Алгоритм получения решения задачи симплекс-методом с использованием офисного приложения Microsoft Excel рассмотрим на примере 2.2.1. Математическая модель задачи имеет следующий вид:

 

 

Для получения решения исходной задачи будем использовать надстройку «Поиск решения».

 

Ввод исходных данных задачи

При решении задачи линейного программирования симплекс-методом с использованием офисного приложения Microsoft Excel необходимо сначала ввести данные задачи. Для этого создается новая рабочая книга Microsoft Excel, в свободные ячейки которой вносятся коэффициенты целевой функции, левой части ограничений, значения правой части ограничений.

Экранная форма для ввода условий задачи имеет следующий вид
(рис. 2.2.2):

 

 

Рис. 2.2.2

 

В ячейках В4:С4 находятся значения коэффициентов целевой функции; в массиве В6:С8 – коэффициенты левой части ограничений; в столбце Е6:Е8 значения правой части ограничений. Ячейки В2:С2 соответствуют переменным задачи, а в ячейке Е2 будет отображаться значение целевой функции. Сюда необходимо ввести формулу, по которой это значение рассчитывается, то есть . Для этого курсор ставится в ячейку и далее набирается следующее выражение: .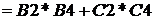

Имена ячеек можно набирать непосредственно с клавиатуры, либо делая на них ссылку мышью.

Значение целевой функции также можно рассчитать, используя надстройку «Мастер функций», а именно, функцию «СУММПРОИЗВ». Для этого необходимо выполнить следующие действия:

поставить курсор в поле Е2;

выбрать на панели инструментов кнопку ;

в окне «Категория» выбрать «Математические». В окне «Выберите функцию» «СУММПРОИЗВ» (рис. 2.2.3) и нажать «ОК»;

 

Рис. 2.2.3

Ввести аргументы функции: в строку «Массив 1» выражение В2:С2, а в строку «Массив 2» выражение В4:С4 (можно, выделять соответствующие массивы с помощью мыши) (рис. 2.2.4) и нажать «ОК»;

 

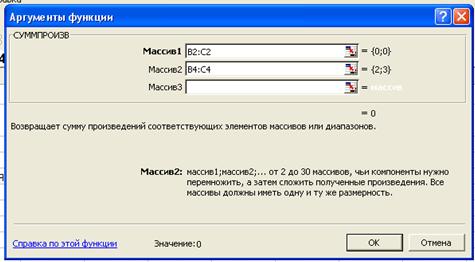
Рис. 2.2.4

После этого в ячейке Е2 появится текущее значение целевой функции, вычисленное по введенной формуле. Оно равно нулю, так как переменные в данный момент равны нулю.

Аналогично в ячейки D6:D8 вводятся формулы для расчета левых частей ограничений (рис. 2.2.5):

 

Рис 2.2.5

 

Для ячейки D6 формула имеет вид , а ее реализация в ячейке: или =СУММПРОИЗВ(В2:C2; В6:C6).

Для ячейки D7 формула имеет вид ,а ее реализация в ячейке: или = СУММПРОИЗВ(В2:C2; В7:C7).

Для ячейки D8 формула имеет вид ,а ее реализация в ячейке: или = СУММПРОИЗВ(В2:C2; В8:C8).

Как видно, формулы для расчета левой части ограничений отличаются друг от друга только именем второго массива (строчки коэффициентов ограничения), первый же массив (массив значений переменных) один и тот же. Поэтому можно ввести формулу один раз, а затем скопировать ее, сделав абсолютную ссылку на массив переменных В2:C2.

Для того, чтобы сделать абсолютную ссылку на определенный столбец, необходимо поставить символ $, перед буквой, обозначающей имя столбца. Например $ В2: $ C2. Чтобы зафиксировать строку, символ $, ставится перед номером строки: В $ 2:C $ 2. Если необходимо сделать абсолютную ссылку на конкретную ячейку (ячейки), символ $ ставится и перед именем столбца и перед номером строки: $ В $ 2: $ C $ 2.

Абсолютную ссылку на ячейку (ячейки) можно сделать, нажав клавишу F4, когда курсор находится в поле имени ячейки. При однократном нажатии клавиши будет сделана абсолютная ссылка на массив или ячейку ($ В $ 2: $ C $ 2). Если клавишу нажать дважды, будет сделана абсолютная ссылка на номер строки (В $ 2: C $ 2). При следующем нажатии клавиши ссылка будет сделана на имя столбца ($ В2: $ C2).

При данном способе реализации симплекс-метода достаточно сделать ссылку лишь на соответствующую строку: В $ 2: C $ 2. В то же время допустима и абсолютная ссылка на конкретный массив ячеек: $ В $ 2: $ C $ 2.

Таким образом, для ячейки D6 формула будет иметь вид или = СУММПРОИЗВ(В$2: C$2;В6:C6) (в случае абсолютной ссылки на массив = СУММПРОИЗВ($В$2: $C$2;В6:C6)).

Затем эту формулу необходимо скопировать в ячейки D7 и D8. Копировать формулу можно с помощью клавиш «Ctrl-Insert» копировать и клавиш «Shift-Insert» вставить. Другой способ копирования формул поставить курсор в ячейку, содержащую формулу и протянуть ее за правый нижний угол на все ячейки, в которые ее необходимо скопировать.

После этого экранная форма условий задачи будет иметь вид (рис. 2.2.6).

 

Рис. 2.2.6

 

Ввод ограничений

Для получения решения задачи используется надстройка «Поиск решения», которая находится в меню «Сервис».

Рис. 2.2.7

В диалоговом окне «Поиск решения» (рис. 2.2.7) необходимо выполнить следующие действия:

Поставить курсор в поле «Установить целевую ячейку» и ввести адрес ячейки, в которой находится формула для расчета значения целевой функции (можно сделать ссылку на ячейку мышью). В примере это ячейка E2.

Выбрать критерий оптимизации целевой функции (максимизация, минимизация или точное значение). В примере это максимум.

Поставить курсор в поле «Изменяя ячейки» и ввести адрес массива, в котором находятся значения переменных. В примере это В2:C2. Адрес можно внести также с помощью выделения мышью соответствующих ячеек.

В окне «Ограничения» выбрать кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 2.6.8).

 

Рис. 2.2.8

 

В поле «Ссылка на ячейку» ввести адрес ячейки, в которой содержится левая часть ограничения. (Это можно сделать путем выделения мышью соответствующей ячейки на экране). В поле знака открыть список предлагаемых знаков и выбрать нужный. В поле «Ограничения» ввести адрес ячейки, содержащей правую часть ограничений. В примере первое ограничение: D6<=E6 в диалоговом окне представлено следующим образом (рис. 2.2.9)

 

Рис. 2.2.9

Нажать кнопку «Д обавить» и аналогично ввести остальные ограничения. Если при вводе ограничений задачи возникает необходимость изменить или удалить ограничения, то для этого используются кнопки «Изменить» и «Удалить» соответственно.

Диалоговое окно надстройки «Поиск решения» после ввода данных имеет следующий вид (рис. 2.2.10)

 

Рис. 2.2.10

Для обеспечения выполнения условия неотрицательности переменных, а также установления конкретных параметров решения задачи оптимизации используется кнопка «Параметры» (рис. 2.2.11)

 

Рис. 2.2.11

Установка флажка «Линейная модель» обеспечивает ускорение процесса решения линейной задачи, а установление флажка «Неотрицательные значения» неотрицательность переменных.

Подтверждаются установленные параметры нажатием кнопки «ОК».

 

Решение задачи

Для решения задачи необходимо в диалоговом окне «Поиск решения» нажать кнопку «Выполнить», после чего на экране появится окно «Результат поиска решения». В случае успешного решения сообщение имеет вид: «Решение найдено. Все ограничения и условия оптимальности выполнены» (рис. 2.2.12)

 

Рис. 2.2.12

Если задача не имеет решения из-за противоречивости системы ограничений или неограниченности целевой функции, сообщение будет иметь вид: «Поиск не может найти подходящего решения» или «Значения целевой ячейки не сходятся» соответственно. Иногда такой результат может быть связан с тем, что в ходе ввода данных были допущены ошибки. Поэтому в случае такого ответа надо проверить правильность ввода данных.

В окне «Результат поиска решения» приведены типы отчета: «Результаты», «Устойчивость», «Пределы», которые используются для анализа чувствительности. Чтобы получить отчет, необходимо выбрать соответствующий тип и нажать кнопку «ОК». Результаты каждого отчета будут выведены на отдельных листах рабочей книги с названиями: «Отчет по результатам 1», «Отчет по устойчивости 1», «Отчет по пределам 1» (рис. 2.2.13)

 

Рис. 2.2.13

 

Если необходимо получить только решение задачи, достаточно нажать кнопку «ОК» в диалоговом окне «Результат поиска решения» (рис. 2.2.12), после чего на экране в соответствующих ячейках появятся значения переменных и целевой функции. В нашем примере значения переменных находятся в ячейках В2:C2,а значение целевой функции – в ячейке E2 (рис. 2.2.14).

 

Рис. 2.2.14

Итак, решение задачи найдено: .

Заметим, что надстройка «Поиск решения» позволяет получать решение и в том случае, если в условии задачи все или некоторые переменные могут принимать только целые значения. Для получения целочисленного решения приведенной выше задачи в описанный процесс необходимо внести некоторые дополнения.

Дополнения вносятся на этапе ввода ограничений. К имеющимся в задаче ограничениям необходимо добавить условие целочисленности переменных. Для этого в диалоговом окне «Поиска решения» надо выбрать кнопку «Добавить», в поле «Ссылка на ячейку» ввести адрес ячеек, содержащих значения переменных (в примере это ячейки В2:С2),а в поле ввода знака ограничения выбрать целое (цел). ( рис.2. 2.15 )

Рис. 2.2.15

 

Подтверждается ввод условия целочисленности нажатием кнопки «ОК». Если задача имеет альтернативное решение, то с помощью компьютера получаем только одно решение.

Чтобы провести анализ чувствительности, необходимо в диалоговом окне «Результаты поиска решения» выделить с помощью мыши требуемый тип отчета: «Результаты», «Устойчивость», «Пределы» (рис. 2.2.16) и нажать кнопку «ОК».

 

Рис. 2.2.16

Результаты каждого отчета будут выданы на отдельных листах рабочей книги (рис. 2.2.17; 2.2.18; 2.2.19).

В таблице «Отчет по результатам» приведена информация о значениях переменных, целевой функции, а также статусе ограничений (рис. 2.2.17).

 

Рис. 2.2.17. Отчёт по результатам (первая таблица)

В первой таблице указано оптимальное значение целевой функции. Результат: 52 000.

Вторая таблица позволяет найти значения переменных принятия решения (результат: ).

В третьей таблице отчета указаны значения левой части ограничений при данных значениях переменных, статус ограничений (связующее или не связующее), а также разность между правой и левой частью. Для связующих ограничений разность равна нулю, для не связующих – больше нуля

«Отчет по устойчивости» состоит из двух таблиц (рис. 2.2.18).

В первой таблице приведена информация о переменных.

1. Результат решения, то есть значения переменных.

2. Нормированная стоимость, или альтернативная цена, которая для небазисных переменных показывает, как изменится значение целевой функции, если соответствующую переменную ввести в базис со значением, равным единице. Для базисных переменных нормированная стоимость равна нулю. В данной задаче обе переменные являются базисными, поэтому их альтернативная цена равна нулю.

3. Коэффициенты целевой функции при соответствующих переменных.

4. Предельные приращения коэффициентов целевой функции, при которых текущее базисное решение не изменится. Так, для переменной границы устойчивости коэффициента целевой функции составляют 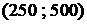, поскольку максимальное увеличение коэффициента возможно на 200, а уменьшение на 50. Другими словами, текущее оптимальное решение не изменится, пока цена за единицу первого вида продукции будет находиться в пределах от 250 до 500 грн.

 

Рис. 2.2.18. Отчёт по устойчивости (вторая таблица)

Вторая таблица содержит данные об ограничениях.

1. В столбце «Результ. значение» указано значение левой части ограничений.

2. В столбце «Теневая цена» находится решение двойственной задачи. Теневая цена показывает, на сколько изменится значение целевой функции, если правая часть ограничения увеличится на одну единицу. В приведенном примере третье ограничение не является связующим, то есть, третий вид сырья используется не полностью. Таким образом, можно закупать его меньше на соответствующую величину, то есть на 100 единиц. Это уменьшит затраты как на закупку сырья, так и на его хранение. Теневая цена первого ограничения, равная 400, свидетельствует о том, что каждая дополнительная единица третьего вида сырья увеличит прибыль на 400 грн. Можно также утверждать, что это максимальная цена, которую можно заплатить за 1 единицу сырья первого вида.

3. В столбцах «Допустимое увеличение (уменьшение)» находятся предельные приращения правых частей ограничений, при которых текущий опорный план не изменится. В примере для первого вида сырья границы устойчивости 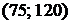, так как допустимое уменьшение возможно на 25 ед., а увеличение на 20 Для второго вида сырья границы устойчивости составляют (100; 140), а для третьего – (200; ) (здесь 1Е+30 равносильна ). Это означает, что, до тех пор, пока количество сырья будет находиться в данных пределах, оптимальное решение задачи не изменится.

«Отчет по пределам» для рассматриваемой задачи имеет следующий вид (рис. 2.2.19):

Рис. 2.2.19. Отчёт по пределам (третья таблица)

Необходимо отметить, что для задач целочисленного программирования отчеты по устойчивости и пределам не применимы.

Необходимо отметить, что при решении задачи с использованием надстройки «Поиск решения» не важно, в какой форме записана задача линейного программирования и содержит ли система ограничений полный единичный базис. Решение осуществляется так, как было описано выше.

 

Для составления и анализа двойственной задачи рассмотрим вначале дополнительно основные понятия двойственности.

При составлении двойственных задач будем пользоваться определением. Если задача задана на max то ограничение вида «£» будем называть согласованным или правильным, а «³» – неправильным, несогласованным. Если задача задана на min, то ограничение «³» – правильное, а «£» – неправильное.

Для написания двойственной задачи сформулируем соотношение между отдельными элементами прямой и двойственной задач:

1. Количество двойственных переменных равно количеству ограничений исходной задачи (каждому ограничению ставится в соответствие двойственная переменная).

2. Целевая функция двойственной задачи имеет вид F = b ₁ y ₁+ b ₂ y ₂+…+ b_my_m.

3. Если Z ® max, то F ® min; если Z ® min, то F ® max (направление цели F противоположно направлению цели Z).

4. Количество ограничений двойственной задачи равно количеству переменных исходной задачи. Каждой переменной исходной задачи ставится в соответствие ограничение двойственной задачи.

5. Левая часть j -го ограничения двойственной задачи равна , а правая с_j. Если 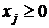, то j -е ограничение в двойственной задаче правильное. Если , то j -е ограничение – неправильное, если имеет любой знак, то j -е ограничение является равенством.

6. Если i -е ограничение исходной задачи правильное, то 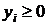, если i -е ограничение исходной задачи неправильное, то , если i -е ограничение исходной задачи «=», то может иметь любой знак.

7. Матрицы исходной и двойственной задач взаимно транспонированные.

Для задачи оптимального выпуска продукции прямая и двойственная записываются в виде:

 

Прямая задача. Двойственная задача.

 

 

Рассмотрим составление двойственной задачи к исходной в общем случае на примере. Написать двойственную задачу к заданной задаче.

 

 

Прямая задача Двойственная задача

 

 

Решение двойственной задачи можно получить, исследуя решение исходной на основании первой и второй теорем двойственности.

Первая теорема двойственности. Если одна из пары двойственных задач имеет оптимальное решение, то вторая также имеет оптимальное решение, причем

 

Если одна из пары двойственных задач не ограничена, то у второй несовместна система ограничений.

Если одна из пары двойственных задач несовместна, то вторая несовместна или неограниченная.

Оптимальные значения переменных двойственной задачи можно определять из индексной строки последней симплексной таблицы по следующему правилу.

Чтобы найти надо:

1) в первой строке первой симплексной таблицы выбрать столбец, в котором находится базисная переменная. Пусть это будет столбец, соответствующий вектору ;

2) в этом столбце взять число, которое находится в индексной строке последней симплексной таблицы, т.е. ;

3) к этому числу прибавить коэффициент целевой функции из этого столбца. Это будет , т.е. .

Аналогично по второй, третьей строке и т. д. первой симплексной таблицы и элементам индексной строки последней таблицы находятся , и т. д.

При нахождении решения двойственной ЗЛП надо пользоваться правилом:

при умножении целевой функции на -1 двойственные переменные меняют знак.

при дописывании балансовых и искусственных переменных значения двойственных переменных не изменяются.

при умножении i -го ограничения на -1 i -я двойственная переменная меняет знак.

Значения двойственных переменных можно выписать из значения теневых цен.

 

4. Напишем двойственную задачу в примере 2.2.1.

5. Находим значения двойственных переменных из табл. 2.2.5.

, .

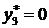Их можно выписать из теневых цен или из индексной строки последней симплекс-таблицы.