Переходим к каноническому виду модели.
Каноническая форма ЗЛП  это форма, которая удовлетворяет трем условиям:
это форма, которая удовлетворяет трем условиям:
все ограничения «=»,
все переменные (х j ³ 0),
Z ®min.
Иногда третье условие пишут в виде Z ® mах.
Для перехода к канонической форме добавляем в левую часть каждого ограничения дополнительную (балансовую) неотрицательную переменную, чтобы преобразовать его в равенство. Преобразовываем и целевую функцию, делая замену 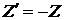 . Балансовые переменные вводятся в целевую функцию с коэффициентом ноль или не пишутся.
. Балансовые переменные вводятся в целевую функцию с коэффициентом ноль или не пишутся.
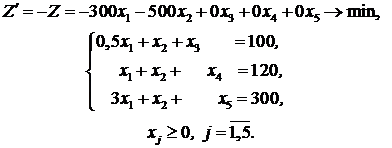
Систему ограничений такого вида является общим решением системы уравнений. В этой системе переменные 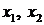 являются свободными, а переменные
являются свободными, а переменные 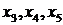
 базисными. Базисным решением называется решение, в котором свободные переменные равны нулю. Базисное решение с неотрицательными компонентами называется допустимым базисным решением или планом. Симплекс-метод решения ЗЛП основывается на теореме, согласно которой оптимальное решение находится на допустимых базисных решениях. Поэтому для решения ЗЛП надо найти начальное допустимое базисное решение и указать правило перехода к новому не худшему.
базисными. Базисным решением называется решение, в котором свободные переменные равны нулю. Базисное решение с неотрицательными компонентами называется допустимым базисным решением или планом. Симплекс-метод решения ЗЛП основывается на теореме, согласно которой оптимальное решение находится на допустимых базисных решениях. Поэтому для решения ЗЛП надо найти начальное допустимое базисное решение и указать правило перехода к новому не худшему.
Если ввести обозначения
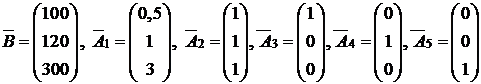 ,
,
то систему ограничений можно записать в векторной форме
 .
.
Это представление является разложением вектора 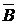 по векторам
по векторам 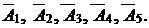 За базис этой системы векторов можно взять систему единичных векторов
За базис этой системы векторов можно взять систему единичных векторов 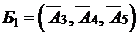 . Допустимое базисное решение будет определять начальный опорный план.
. Допустимое базисное решение будет определять начальный опорный план.
Выпишем начальный опорный план и значение целевой функции для него. Для этого свободные переменные приравниваем к нулю: 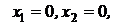 а базисные переменные после этого находят из системы:
а базисные переменные после этого находят из системы:
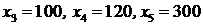 .
.
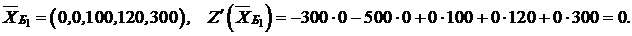
Решение задачи принято оформлять симплекс-таблицами.
Таблица 2.2.2. Первая симплекс-таблица задачи 2.2.1
| ¯ | |||||||||||
 | 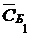 | 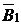 | 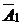 | 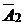 | 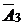 | 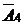 | 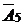 | 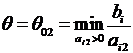 | |||
 300 300 |  500 500 | ||||||||||
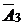 | 0,5 | [1] | 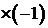 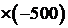 | ||||||||
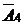 |  | | | ||||||||||
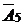 | 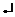 | | | ||||||||||
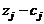 | 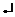 |
Индексная строка рассчитывается следующим образом:
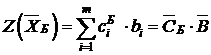 ,
,
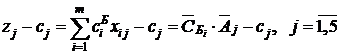 .
.
В первой симплексной таблице имеем
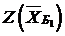 = 0×100+0×120+0×300 = 0, z 1- c 1 = 0×0,5+0×1+0×3– (–300) =300,
= 0×100+0×120+0×300 = 0, z 1- c 1 = 0×0,5+0×1+0×3– (–300) =300,
z 2- c 2 = 0×1+0×1+0×1– (–500) = 500, z 3- c 3 = 0×1+0×0+0×0–0 = 0,
z 4- c 4 = 0×0+0×1+0×0  0 = 0, z 5- c 5 = 0×0+0×0+0 – 0 = 0.
0 = 0, z 5- c 5 = 0×0+0×0+0 – 0 = 0.
Симплексная таблица составляется следующим образом. В первой строке шапки симплекс-таблицы указаны векторы исходной системы ограничений задачи, а во второй – коэффициенты при переменных в целевой функции задачи. В первом столбце (столбец 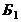 ) указаны векторы, образующие базис заданной системы векторов, а во втором – коэффициенты целевой функции при базисных переменных. Во всех остальных клетках таблицы (кроме последней строки, о которой будет сказано далее) стоят коэффициенты разложения соответствующих векторов по векторам базиса.
) указаны векторы, образующие базис заданной системы векторов, а во втором – коэффициенты целевой функции при базисных переменных. Во всех остальных клетках таблицы (кроме последней строки, о которой будет сказано далее) стоят коэффициенты разложения соответствующих векторов по векторам базиса.
Так как для нашей задачи выбран единичный базис, то в первой симплексной таблице в столбцах 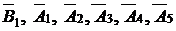 будут стоять соответствующие коэффициенты системы ограничений.
будут стоять соответствующие коэффициенты системы ограничений.
Последняя строка называется индексной или 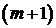 -й. Во втором столбце этой строки стоит значение целевой функции при проверяемом опорном плане. В нашем случае
-й. Во втором столбце этой строки стоит значение целевой функции при проверяемом опорном плане. В нашем случае 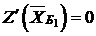 . Во всех остальных клетках индексной строки находятся оценки оптимальности
. Во всех остальных клетках индексной строки находятся оценки оптимальности 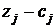 для векторов исходной системы. Здесь
для векторов исходной системы. Здесь 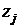 – значение целевой функции, если в неё вместо переменных подставить коэффициенты разложения вектора
– значение целевой функции, если в неё вместо переменных подставить коэффициенты разложения вектора 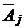 по векторам базиса, а
по векторам базиса, а 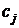 – коэффициенты целевой функции при соответствующих переменных.
– коэффициенты целевой функции при соответствующих переменных.
Число 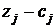 показывает, на сколько уменьшиться значение целевой функции, если переменную
показывает, на сколько уменьшиться значение целевой функции, если переменную 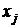 увеличить на единицу.
увеличить на единицу.
Отсюда следует правило проверки решения на оптимальность:
1) проверяем знаки 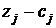 ;
;
2) если все 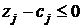 , то оптимальное решение найдено, есть минимум Z;
, то оптимальное решение найдено, есть минимум Z;
3) если имеются 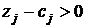 , то составляем новую симплексную таблицу и опять проверяем знаки чисел в индексной строке. Итерации продолжаем до тех пор, пока не получим в индексной строке все неотрицательные числа или установим отсутствие конечного решения задачи (
, то составляем новую симплексную таблицу и опять проверяем знаки чисел в индексной строке. Итерации продолжаем до тех пор, пока не получим в индексной строке все неотрицательные числа или установим отсутствие конечного решения задачи (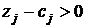 , а все числа
, а все числа 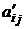
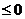 для некоторого j).
для некоторого j).
Проверяем первый опорный план на оптимальность.
Из-за того, что в индексной строке есть положительные числа, то он не оптимален.
Переходим к новому плану. Вектор, вводимый в базис, выбираем по наибольшему числу в индексной строке. Это есть вектор 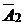 .
.
Вектор, выводимый из базиса, выбираем по симплексному отношению.
В общем виде симплексное отношение для 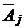 находится по формуле
находится по формуле
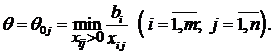
В нашем случае
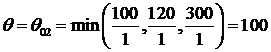 .
.
Симплексное отношение находится лишь для положительных 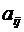 . Таким образом, из базиса выводим вектор
. Таким образом, из базиса выводим вектор 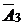 .
.
Столбец, в котором находится вектор, вводимый в базис, называется разрешающим, строка, в которой находится вектор, выводимый из базиса  разрешающей. Элемент, находящейся на пересечении разрешающего столбца и строки – разрешающим элементом.
разрешающей. Элемент, находящейся на пересечении разрешающего столбца и строки – разрешающим элементом.
Разрешающий элемент выделен квадратными скобками и жирно.
Составляем новую симплексную таблицу. Для этого пересчитываем коэффициенты исходной системы по методу полных жордановых исключений. Это правило состоит в следующем.
В столбце 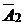 мы должны получить единичный столбец. Для этого разрешающую строку вычитаем из второй и третьей строк.
мы должны получить единичный столбец. Для этого разрешающую строку вычитаем из второй и третьей строк.
В общем, при составлении новой симплекс-таблицы надо разрешающую строку поделить на разрешающий элемент, разрешающий столбец заменить единичным столбцом с единицей на месте разрешающего элемента. Элементы, которые находятся не в разрешающей строке и столбце, иногда удобно пересчитывать по правилу прямоугольника (вторая модификация правила полных Жордановых исключений):
Таблица2.2.3. Правило прямоугольника
  apr apr | … |  apj apj | 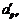 | … | ||
| … | … | 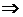 | … | … | ||
 air air | … | [ aij ] | 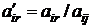 | … |
Правило прямоугольника состоит из следующих шагов.
1) Элементы разрешающей i- й строки делим на разрешающий элемент таблицы 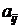 .
.
2) Для того чтобы в направляющем столбце все остальные элементы стали равными нулю, элементы полученной строки умножаем последовательно на 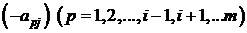 и прибавляем к соответствующем элементам p -й строки. Тогда вместо числа
и прибавляем к соответствующем элементам p -й строки. Тогда вместо числа 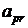 в p- й строке станет число
в p- й строке станет число
3) 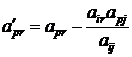 или
или 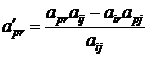 .
.
Числитель в этой формуле вычисляется как определитель второго порядка, за первую диагональ надо брать диагональ, на которой находится пересчитывающийся элемент. Например,
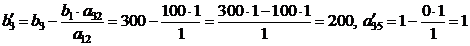
Для контроля индексную строку можно также пересчитывать по этому правилу. В нашем случае разрешающую строку умножаем на (-500) и прибавляем к индексной строке. Схема этих вычислений изображена справа от табл. 2.2.1.
После проведённых вычислений получили вторую симплекс-таблицу, табл. 2.2.4.
Таблица 2.2.4. Вторая симплекс-таблица задачи 2.2.1
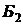 | 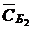 | 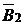 | 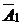 | 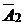 | 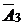 | 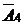 | 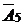 | 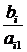 | |||
 300 300 |  500 500 | ||||||||||
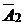 |  500 500 | 0,5 | 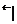 | ||||||||
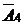 | [0,5] |  1 1 | 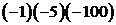 | ||||||||
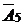 | 2,5 |  1 1 | 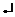 | | | ||||||||
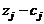 |  50000 50000 |  500 500 | 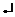 |
Получили второе опорное решение:
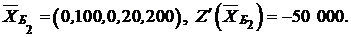
Значение целевой функции на втором шаге решения уменьшится на величину 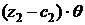 , т.е.
, т.е.
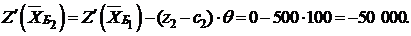
Второе опорное решение не является оптимальным, так как в индексной строке есть положительное число. Аналогично предыдущему переходим к третьему опорному плану. В базис вводим вектор 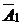 , а из базиса выводим вектор
, а из базиса выводим вектор 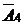 . Для этого разрешающую строку умножаем на (-1), (-5), (-100) и прибавляем соответственно к первой, третьей и индексной строке. Индексную строку для контроля можно находить по правилу расчёта индексной строки.
. Для этого разрешающую строку умножаем на (-1), (-5), (-100) и прибавляем соответственно к первой, третьей и индексной строке. Индексную строку для контроля можно находить по правилу расчёта индексной строки.
Получили третью симплексную таблицу.
Таблица 2.2.5. Третья симплекс-таблица задачи 2.2.1
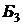 | 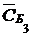 | 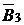 | 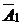 | 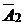 | 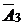 | 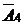 | 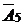 | |
 300 300 |  500 500 | |||||||
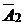 |  500 500 |  1 1 | ||||||
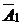 |  300 300 | -2 | ||||||
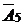 |  5 5 | |||||||
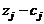 |  52 000 52 000 |  400 400 |  100 100 | |||||
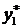 | 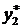 | 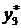 |
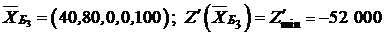
или
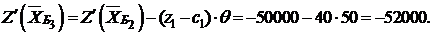
Третий план оптимален и единственный, потому что свободные вектора имеют отрицательные оценки.
Из табл. 2.2.5 выписываем значение целевой функции и оптимальное значение переменных задачи 2.2.1.
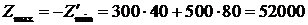 ,
, 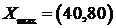 .
.
 2017-11-30
2017-11-30 1103
1103
