Производной функции у=f(х) в т. Х0 называется предел отношения приращения ф-ции в этой точке к приращению аргумента при ∆х→0, т.е. 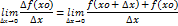
Геометрический смысл: производная в т. Х0 равна угловому коэффициенту касательной к графику функции у=f(x) в этой точке f 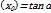
Уравнение касательной к графику функции y=f(x) в т. Х0: y= f(x0) + f ‘(x0)(x-x0)
Физический смысл производной: производная функции у=f(х) в точке Х0 – это скорость изменения функции f(х) в т. Х0: V(t)=x'(t)
11. Понятие дифференцируемости функции.
Связь между понятиями дифференцируемости и непрерывности.
Функция у=f(х) называется дифференцируемой в точке х0, если ее приращение в этой точке можно представить в виде: ∆у=А∆х+0(∆х), где А- некоторая постоянная, а 0(∆х) – является бесконечно малой при ∆х→0.
Теорема о дифференцируемости: Для того чтобы функция у=f(x) была дифференцируема в т. Х0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Cвязь между понятиями дифференцируемости и непрерывности. Имеет место следующая теорема. Если функция y=f(x) дифференцируема в точке х0, то она непрерывна в этой точке.
Доказательство. Так как функция y=f(x) дифференцируема в точке x0, то существует конечный предел 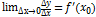 . Тогда по теореме о связи бесконечно малой с функцией, имеющей конечный предел, будем иметь
. Тогда по теореме о связи бесконечно малой с функцией, имеющей конечный предел, будем иметь
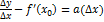 , где a(∆x) - бесконечно малая величина при ∆x→ 0.
, где a(∆x) - бесконечно малая величина при ∆x→ 0.
Откуда ∆y=f '(x0)∆x + a(∆x)*∆x
Переходя в этой формуле к пределу при ∆х→0, получим по свойствам бесконечно малых, что 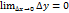
Следовательно, по одному из определений непрерывности функция y=f(x) в точке x0 является непрерывной. Обратная теорема, вообще говоря, неверна, т.е. функция может быть непрерывной в данной точке, но не быть дифференцируемой в этой точке.
12. Правила дифференцирования суммы,
разности, произведения и частного.
Если существуют производные U'(x) и V'(x), то производная от суммы(разности) этих функций равна сумме (разности) производных:
(u(x)±v(x))’=u’(x) ± v’(x)
Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов.
Если существуют производные U'(x) и V'(x), то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
(U*V)'=U'V+ UV'; (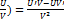
 2017-10-25
2017-10-25 1246
1246
