2017-10-25
6475
Теорема о производной обратной функции: Если функция у=f(x) имеет производную в т. Х0, где f''(x0)≠0, то функция х=f-1(y) имеет также производную в этой точке, причем (f-1(y0))'= 
Теорема о производной сложной функции. Пусть функция u=u(x) имеет производную в точке х0 , а функция y=f(u) имеет производную в точке uo=u(xo). Тогда сложная функция y=f(u(x)) имеет производную в точке х0, причем y’=f ’(uo)•u’(xo)
Данная формула может быть распространена на конечное число суперпозиций.
16. Производные показательной и обратных
тригонометрических функций.
Производная показательной функции: у=ах, у'=ахlna
Производные обратных тригонометрических ф-ций: (arcsinx)’= 
x(y)=sin y; x'(y)=cos y= 
; y'= 
(arccosx)’= 
(arctgx)’= 
x'(y)=tg y, x'(y)= 
; y'= 
(arcctgx)’= 
Логарифмическая производная. Производная степенной функции.
Логарифмическая производная.
y=ln U; y'=(ln U)'= 
Для примера найдем производную показательно степенной функции x в степени x.
Логарифмирование дает ln y=ln xx. По свойствам логарифма ln y=x*ln x. Дифференцирование обеих частей равенства приводит к результату:
ln y=x*ln x
(ln y)'=(x*ln x)'
*y'=x'*ln x+ x*(ln x)'
y'=y*(1*ln x+x* 
=y*(ln x+1)=xx*(ln x+1).
Формула производной степенной функции имеет вид (x)' = n * xn-1, где показатель степени p – любое действительное число.
ln y=ln xn=n* ln x; 
; y'=ny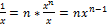 
Таблица производных простейших элементарных функций.
| f(kx+b) | f’(kx+b) | ctg(kx+b) |  |
| (kx+b)p | kp(kx+b)p-1 | arcsin(kx+b) |  |
| ekx+b | kekx+b | arccos(kx+b) |  |
| akx+b | kakx+blna | arctg(kx+b) |  |
| ln(kx+b) |  | arcctg(kx+b) |  |
| loga(kx+b) |  | sh x | ch x |
| sin(kx+b) | k cos(kx+b | ch x | sh x |
| cos(kx+b) | -k sin(kx+b) | th x |  |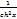
| tg(kx+b) |  | cth x |  |
