Определение: Дифференциалом dy функции y = f(x) в точке x называют главную, линейную относительно ∆x, часть ее приращения ∆y, которая равна произведению производной функции в этой точке на приращение аргумента: dy = f''(x)*∆ х. Для производной существует запись: f''(x0)= 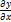
Геометрически дифференциал функции y = f(x) в точке x равен приращению ординаты касательной к графику функции в рассматриваемой точке, когда переменная x получает приращение ∆x. Основные формулы, которые связаны с дифференциалами, можно получить, используя связь между дифференциалом функции и ее производной, то есть тот факт, что dy = y'(x)dx, а также соответствующие формулы для производных. Рассмотрим две дифференцируемые функции u(x) и v(x). Тогда имеют место следующие равенства:
| 1. d(u + v) = du + dv; 2. d(uv) = u*dv + v*du; | 3. d 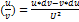 ; 4. d(cy(x)) = cd(y(x)). ; 4. d(cy(x)) = cd(y(x)). |
14. Производные постоянной, тригонометрических и
логарифмической функций.
При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем x0=x, где x – любое действительное число, то есть, x – любое число из области определения функции f(x)=C. Запишем предел отношения приращения функции к приращению аргумента при ∆x→0: 
Таким образом, производная постоянной функции f(x)=C равна нулю на всей области определения.
Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:



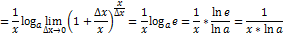
В частности, при а=е имеем у=ln x, (ln x)'= 
По определению производной для функции синуса имеем

Воспользуемся формулой разности синусов:


Осталось обратиться к первому замечательному пределу:

Абсолютно аналогично доказывается формула производной косинуса.


Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования
tg'x= 
ctg'x= 
 2017-10-25
2017-10-25 1071
1071








