2017-10-25
1991
 |
Вторая теорема Карно позволяет вычислить термический коэффициент полезного действия машины Карно, взяв в качестве рабочего тела идеальный газ. В координатах
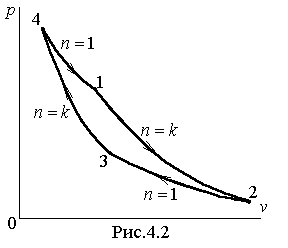
цикл такого двигателя, состоящий из двух изотерм и двух адиабат, показан на рис.4.2.
Здесь процесс 1–2 есть адиабатическое расширение со снижением температуры рабочего тела от температуры T 1 верхнего источника тепла до температуры T 2 нижнего источника, 2–3 – изотермическое сжатие с отводом тепла нижнему источнику с постоянной температурой T 2, 3–4 – адиабатическое сжатие с повышением температуры от T 2 до T 1, 4–1 – изотермическое расширение с подводом теплоты к рабочему телу при постоянной температуре верхнего источника T 1.
Используя результаты расчета изотермического и адиабатического процессов идеального газа, находим термический КПД этого цикла:
(4.9)
С другой стороны, для двух адиабатных процессов 1–2 и 3–4 имеем
Таким образом, термический КПД цикла Карно для идеального газа, а значит, и для любого другого рабочего тела, определяется следующим выражением:
(4.10)
Полученная формула является чрезвычайно важной для анализа работы любого теплового двигателя, а также во многих других отраслях теоретической науки – от биофизики до космологии, т.к. она определяет верхний предел совершенствования эффективности превращения теплоты в работу, т.е. неупорядоченной формы движения материи, каковой является теплота, в упорядоченную форму, например, механическое перемещение, электроэнергия и др.
Из определения термического КПД теплового двигателя (4.6) и выражения (4.10) для термического КПД цикла Карно получаем
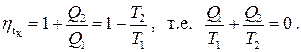(4.11)
Отношение количества теплоты в изотермическом процессе к абсолютной температуре этого процесса было названо Р.Клаузиусом приведенным теплом. Таким образом, в отношении цикла Карно можно сказать, что сумма приведённых теплот для него равна нулю.
4.8. Интеграл Клаузиуса. Энтропия
Рассмотрим произвольный обратимый цикл некоторого теплового двигателя, изображённый на рис.4.3. Его можно осуществить только в случае, если количество верхних и нижних источников тепла достаточно велико (в пределе бесконечно велико).
Разобьём мысленно этот цикл системой близких (в пределе бесконечно близких) адиабат и изотерм. Тогда произвольный цикл можно представить набором достаточно узких (в пределе бесконечно узких) циклов Карно, работающих при различных температурах верхних и нижних источников тепла.
 |
Для 
узкого цикла Карно имеем на основании (4.11)
Суммируя это равенство по всем N узким циклам Карно, получим
Переобозначив индексы, эту сумму можно переписать в виде
В пределе 
эта сумма преобразуется в интеграл по замкнутому контуру (циклу)
(4.12)
Этот результат носит название интеграла Клаузиуса.
Как известно из математики, тождественное равенство нулю интеграла по произвольному замкнутому контуру (4.12) говорит о том, что стоящий под знаком интеграла дифференциал 
является полным, т.е. можно записать
(4.13)
С физической точки зрения тот факт, что дифференциал некоторой функции является полным, говорит о том, что сама функция есть свойство системы, функция её состояния, т.е. её значение может быть вычислено или измерено в данном состоянии системы, зависит только от параметров состояния и не зависит от пути, которым данное состояние было достигнуто. По предложению Р.Клаузиуса, функция 
, 
, 
была названа энтропией. Таким образом, любая термодинамическая система, любое макроскопическое тело, кроме уже известных термодинамических параметров 
, обладает ещё одной функцией состояния – энтропией, которая, как следует из (4.13), позволяет записать выражение для количества теплоты в виде, подобном записи выражения для работы, т.е. как произведение некоторого потенциала на изменение "координаты":
(4.14)
Так же как и количество теплоты, энтропия обладает свойством аддитивности, поэтому можно ввести в рассмотрение удельную энтропию s
(4.15)
Размерность энтропии, как это следует из (4.13), совпадает с размерностью теплоёмкости, однако по смыслу теплоёмкость и энтропия не совпадают. Выяснение физического смысла энтропии выходит за рамки термодинамики; мы обсудим этот вопрос ниже.
4.9. Неравенство Клаузиуса. Математическое выражение II начала термодинамики
Помимо цикла Карно, работающего в интервале температур верхнего источника тепла T 1 и нижнего источника тепла T 2 и имеющего, как мы выяснили, максимально возможный в данном интервале температур термический КПД, рассмотрим какой-либо другой цикл, функционирующий в том же интервале температур. Как следует из первой теоремы Карно, термический КПД такого цикла заведомо будет ниже термического КПД цикла Карно, а сам цикл заведомо будет необратимым. Имеем тогда неравенство
откуда следует, что сумма приведённых теплот для необратимого цикла отрицательна:
(4.16)
Рассуждая аналогично тому, как мы это делали при выводе интеграла Клаузиуса (4.12), т.е. рассматривая произвольный необратимый цикл и разбивая его мысленно множеством адиабат на большое (в пределе бесконечное) число циклов с различными значениями температур верхних и нижних источников тепла, получим неравенство Клаузиуса
(4.17)
Ноль в правой части этого неравенства есть не что иное, как интеграл по замкнутому контуру от дифференциала энтропии для обратимого цикла, т.е.
откуда, ввиду произвольности контура интегрирования, получаем
(4.18)
Это неравенство говорит о том, что изменение энтропии вещества в любом необратимом процессе всегда больше приведённой теплоты этого процесса. Для конечного процесса будем иметь
(4.19)
Результаты (4.13),(4.18) объединим в одной записи, которую можно считать математической формулировкой второго начала термодинамики: 
(4.20)
Здесь знак (=) относится к обратимым процессам, а знак (>) – к необратимым.
Существование энтропии или, что то же самое, невозможность построения вечного двигателя второго рода, говорит о том, что дифференциальная форма для количества тепла
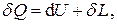
где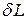 
представляет в общем случае сумму всех известных на настоящее время видов работ, не будучи полным дифференциалом, обладает тем не менее интегрирующим множителем, равным 
.
8. К следующему занятию курсанты должны:
ЗНАТЬ: основные элементы и количественные характеристики термодинамической эффективности теплового двигателя; суть и математическое выражение второго начала термодинамики.
УМЕТЬ: применять математический аппарат термодинамики и графический метод диаграмм к расчету обратимых циклов тепловых двигателей.
ИМЕТЬ ПРЕДСТАВЛЕНИЕ: об эквивалентности различных формулировок второго начала термодинамики и о необратимости реальных процессов.
Задания на самоподготовку:
· конспект лекций
· задача на применение второго начала термодинамики
Подпись автора
___________/ профессор каф. физики и теплообмена П.В. Скрипов
Лекция рассмотрена и одобрена на заседании кафедры
Протокол №_______ от «_____»_____________2006 г.
Зав. кафедрой физики и теплообмена
профессор, д.т.н. __________________ / Н.М. Барбин
«_____»______________ 2006 г.
