Характеристические функции

МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО ДЕЛАМ ГРАЖДАНСКОЙ ОБОРОНЫ,

ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ

СТИХИЙНЫХ БЕДСТВИЙ

УРАЛЬСКИЙ ИНСТИТУТ ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ

 

 

Кафедра физики и теплообмена

 

 

Дисциплина:

ТЕПЛОТЕХНИКА

 

Л Е К Ц И Я

 

ТЕМА 5. ФАЗОВЫЕ ПЕРЕХОДЫ. ПРОЦЕССЫ ВОДЯНОГО ПАРА

 

Автор:

д.ф.-м.н., профессор П.В. Скрипов

 

 

Екатеринбург 2006

Цели лекции:

 

Учебные: Сформировать представление об основных условиях термодинамического равновесия и дать концепцию термодинамики фазовых переходов; познакомить с методом термодинамических потенциалов и процессами водяного пара.

 

Воспитательные: Воспитывать стремление к углубленному изучению предмета; прививать убежденность в практической значимости получаемых в лекционном курсе знаний.

 

Развивающие: Развивать способность творчески воспринимать и конспектировать предоставляемый материал; развивать навыки самостоятельной аналитической работы, умение выделять главное, проводить сопоставление и обобщение.

 

Метод проведения: лекция

Время занятия: 160 минут

Место проведения: аудитория

Материальное обеспечение: раздаточный материал с представлением основных соотношений и графиков

 

ЛИТЕРАТУРА:

1. Теплотехника: Учебник для вузов / А.П. Баскаков, Б.В. Берг, О.К. Витт и др.; под ред. А.П. Баскакова. 2-е изд., перераб. – М.: Энергоатомиздат, 1991. 224 с.

2. Техническая термодинамика: Учебное пособие / В.Н.Королёв, Е.М.Толмачёв. Екатеринбург: УГТУ, 2001. 180 с.

 

ПЛАН ЛЕКЦИИ:

1. Введение. Термодинамика фазовых переходов.

2. Уравнение Гиббса.

3. Характеристические функции. Термодинамические потенциалы.

4. Условия термодинамического равновесия однофазной системы.

5. Химический потенциал.

6. Условия термодинамического равновесия многофазных систем.

7. Фазовый переход "жидкость - пар".

8. Формула Клапейрона – Клаузиуса.

9. Параметры влажного пара.

10. Процессы водяного пара. Диаграмма .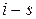

 

Уравнение Гиббса

Первое и второе начала термодинамики и математические свойства дифференциалов теплоты, работы, внутренней энергии, энтальпии, энтропии позволяют развить математически строгий формализм исследования термодинамических свойств веществ и процессов изменения их состояния. Начала термодинамики могут быть записаны совместно в одной из форм:

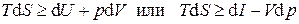, (5.1)

где знак равенства относится к обратимым процессам, а знак неравенства - к необратимым. В случае обратимых процессов эти соотношения носят название термодинамических тождеств или фундаментальных уравнений Гиббса:

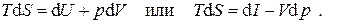(5.2)

Из уравнений Гиббса можно получить несколько весьма важных для практических целей результатов. Запишем для этого (5.2) в виде

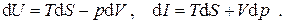(5.3)

Применив к этим выражениям преобразование Лежандра по переменным 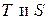, т.е. имея в виду, что 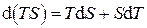, получим

Новые функции состояния

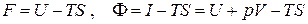(5.4)

носят названия свободной энергии Гельмгольца (F) и свободной энергии Гиббса ( Φ ). Имеем, таким образом, ещё две дифференциальные формы:

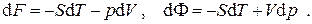(5.5)

Так как (5.3) и (5.5) есть полные дифференциалы функций двух переменных 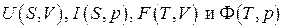, то из сравнения коэффициентов при дифференциалах независимых переменных получаем соотношения, связывающие частные производные от функций, характеризующих термодинамическую систему, по одним независимым переменным с другими независимыми переменными:

(5.6)

Характеристические функции

Каждая из функций 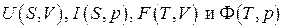носит название характеристической функции, а пара независимых переменных при них называется естественной парой переменных параметров для соответствующей характеристической функции. Все они, естественно, однозначно связаны друг с другом в соответствии с их определением (5.4).

Характеристические функции играют важную роль в исследовании термодинамических систем, так как знание их позволяет вычислять термодинамические параметры вещества простым дифференцированием. Сами же характеристические функции находятся либо экспериментальным путём, либо теоретически с помощью методов статистической физики.

Далее, из того факта, что дифференциалы характеристических функций являются полными, следует равенство перекрёстных производных:

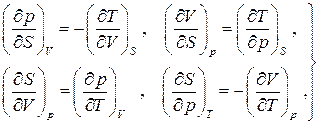
(5.7)

называемых соотношениями Максвелла. Эти соотношения позволяют сводить нахождение трудно измеримых в опыте производных к относительно просто измеримым. В дальнейшем мы воспользуемся ими при исследовании свойств водяного пара.