Примеры решения задач. Задача 1.Проверить справедливость равенства А (ВÇС) = (А В) Ç (А С)

Задача 1. Проверить справедливость равенства А \ (В Ç С) = (А \ В) Ç (А \ С).

Решение. Строим диаграммы Венна отдельно для множества, заданного в левой части проверяемого равенства, и для множества в правой части (рис. 1).

Рис. 1

 

В левой части пересечение (В Ç С) показано частой косой штриховкой, разность А \ (В Ç С) - редкой штриховкой. В правой части разность (А \ В) показана вертикальной штриховкой, разность (А \ С) – горизонтальной штриховкой, их пересечение (А \ В) Ç (А \ С) – область, заштрихованная дважды (в клеточку). Сравнение обоих рисунков показывает, что левая и правая части равенства – разные. Следовательно, равенство не верно: А \ (В Ç С) ≠ (А \ В) Ç (А \ С).

Из этих же чертежей можно заключить, что множество в левой части равенства совпадает с объединением двух разностей из правой части (А \ В) È (А \ С).

Задача 2. Опрос 100 студентов показал, что 52 пользуются домашним компьютером, 71 – мобильным телефоном, 12 – ни тем, ни другим. Сколько студентов используют оба прибора, только компьютер, только телефон?

Решение. Решение этой задачи связано с формулой числа элементов в объединении двух, вообще говоря, пересекающихся множеств: ½ А È В ½= ½ А ½ + ½ В ½ – ½ А Ç В ½.

Требуется выразить число элементов пересечения (рис. 2):

½ А È В ½= ½ А ½ + ½ В ½ – ½ А Ç В ½Þ½ А Ç В ½= ½ А ½ + ½ В ½ – ½ А È В ½

Рис. 2

 

Строим диаграмму Венна. Из условия следует, что число элементов объединения равно
100 – 12 = 88. Результаты получаем подстановкой числовых данных в формулу:

½ А È В ½= 100 – 12 = 88;

½ А Ç В ½= 52 + 71 – 88 = 35;

½ А \ В ½= 52 – 35 = 17;

½ В \ А ½= 71 – 35 = 36.

Оба прибора используют 35 студентов, только компьютер – 17, только телефон – 36.

Задача 3. Что называется декартовым произведением двух множеств? Найти и показать на координатной плоскости произведение А В, где А = [3, 5], В = [1, 4]: А и В – множества либо дейcтвительных чисел R, либо натуральных чисел N: а) А, В Í N; б) A, B Í R; в) A Í N, B Í R;
г) A Í R, B Í N.

Решение. Декартово произведение А ´ В двух множеств – это множество всех пар (x, y), где
x Î A, y Î B.

На рисунке 3, б произведение А ´ В изображается прямоугольником, проекция которого на ось абсцисс – множество А, а проекция на ось ординат – множество В.

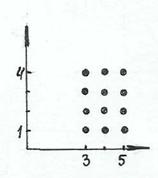
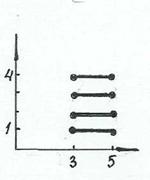
а) б) в) г)

Рис. 3

 

Если же А и В – множества целых чисел А = [3, 5], В = (1, 4); А, В Í Z, то произведение
А ´ В – прямоугольник, составленный из целочисленных точек, т.е. точек, у которых обе координаты – целые числа (рис. 3, а).

Для точек на рис. 3, в, г одна из координат дискретная, другая – непрерывная.

Задача 4. Устанавливает ли функция y = cos x взаимно однозначное соответствие между отрезками [-π/2, π/2] и [0, 1]?

Решение. Используем графическое представление основной элементарной функции y = cos x (рис. 4). На участке [-π/2, π/2] функция принимает все значения из отрезка [0, 1]. Но любое значение, кроме у = 1, функция принимает в двух точках: например, cos(-π/2) = cos(π/2) = 0.

Рис. 4

 

Следовательно, взаимно однозначного соответствия на этом множестве нет.

Если же рассмотреть ту же функцию на множестве [0, π/3], то она осуществляет взаимно однозначное соответствие с отрезком [1/2, 1]. Это видно на графике.

Задача 5. Пусть f (X) = 2 ^X, g (X, Y) = X - Y. Что выражают суперпозиции h ₁(X, Y) = f (g (X, Y)), h ₂(X, Y) = g (f (Y), f (X)), h ₃(X) = f (g (X, f (X)))?

Решение. h ₁(X, Y) = f (g (X, Y)) = f (X – Y) = 2 ^X-Y.

h ₂(X, Y) = g (f (Y), f (X)) = f (Y) - f (X) = 2 ^Y - 2 ^X.

h ₃(X) = f (g (X, f (X))) = 2 ^{g (X, f (X))} = 2 ^{X - f (X)} = 2 ^{X -}

Задача 6. Построить схемы из функциональных элементов, реализующие суперпозиции
h ₂(X, Y) = g (f (X), f (Y)), h ₃(X) = f (g (X, f (X)))из предыдущей задачи.

Решение. Используются одновходовые элементы, реализующие возведение константы 2 в степень Х, и двухвходовый элемент, реализующий вычитание (рис. 5).

h ₂(X, Y) = 2 ^X - 2 ^Yh ₃(X) = 2 ^{X - .}

Рис. 5

 

В первом случае внешняя функция (соответственно, последний элемент в схеме) – вычитание. Во втором случае внешняя функция – возведение в степень.

Задача 7. Построить схему из функциональных элементов для вычисления объема V и полной поверхности S прямоугольного параллелепипеда, у которого длина, ширина и высота соответственно равны a, b, c.

Решение. Выражаем V и S формулами: V = a • b • c; S = 2 (a • b + a • c + b • c).

Схема (рис. 6) реализует обе формулы, причем некоторые элементы (здесь – элемент, вычисляющий произведение a • b) могут быть использованы при вычислении обеих величин.

Рис. 6

Поэтому выход элемента разветвляется.

Задача 8. Какие соединения элементов данной схемы из функциональных элементов (рис. 7) являются ошибочными?

Рис. 7

Решение. 1. Элемент S ₁ – реализует одноместную функцию lg t; он не должен иметь
двух входных полюсов.

2. Элемент S ₃ – реализует двуместную функцию (s + t); он должен иметь два входных полюса.

3. На вход элемента S ₄ не должны поступать два разных значения (в данном случае с входного полюса Y и выхода элемента S ₂).

4. На единственный выход схемы не должны поступать два разных значения (в данном случае с выходов элементов S ₃ и S ₄).

Задача 9. Какую функцию реализует схема из функциональных элементов (рис. 8)?

Рис. 8

Решение. 1) S ₁ = lg X;

2) S ₂ = Z – Y;

3) S ₃= S ₁• Z = (lg X) • Z;

4) S ₄ = (S ₂)³ = (Z – Y)³;

5) S ₅ = S ₃ + S ₄ = Z • (lg X) + (Z – Y)³.

Искомая функция – на выходе элемента S ₅.

Задача 10. x – вектор на плоскости; А (x), В (x) – одноместные алгебраические операции:
А (x) = х – b, где b = (2, 3); В (x) = 2∙ x. Какие векторы представляются суперпозициями этих операций A (A (x)), B (A (B (x))), A (B (A (x))), A (B (A (B (x)))), если х – вектор (5, 3)?

Решение. Применение операции A к вектору z - вычитание вектора (2, 3).

(А (x) = х – b = (5, 3) – (2, 3) = (3, 0).

Применение операции В к вектору z - удвоение. В (х) = 2∙ х = 2 ∙ (5, 3) = (10, 6).

Далее – применение этих операций к результату предыдущей операции. На рис. 9 – графическое представление суперпозиций.

А (А (x) = (х – b) – b = (3, 0) – (2, 3) = (1, -3);

А (В (x)) = (2 х – b) = (10, 6) – (2, 3) = (8, 3);

В (А (x)) = 2 ∙ (х – b) = 2 ∙ (3, 0) = (6, 0);

В (А (В (x))) = 2 ∙ (2 х – b) = 2 ∙ (8, 3) = (16, 6);

А (В (А (x))) = 2 ∙ (х – b) – b = (6, 0) – (2, 3) = (4, -3);

А (В (А (В (x)))) = 2 ∙ (2 х – b) – b = (16, 6) – (2, 3) = (14, 3).

Рис. 9

 

Задача 11. Пусть R – бинарное отношение на множестве М из 12 натуральных чисел
{4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24}: «xRy, если x¹y и х делится на у без остатка».

Сколько пар (x, y), элементы которых находятся в отношении xRy?

Является ли отношение xRy отношением эквивалентности?

Решение. Перечислим все такие пары: (8, 4), (10, 5), (12, 4), (12, 6), (15, 5), (16, 4), (16, 8),
(18, 6), (18, 9), (20, 4), (20, 5), (20, 10), (24, 4), (24, 6), (24, 8), (24, 12). Таким образом, их число - 16. Для ответа на вторую часть вопроса нужно проверить выполнение трех свойств, которыми должно обладать отношение эквивалентности. Транзитивность отношения выполняется: если x делится на y и y делится на z, то x делится на z; однако, рефлексивность отношения не выполняется в силу условия (отношение xRy не выполняется для равных x, y); отношение xRy также несимметрично: если x делится на y, то x>y, и поэтому y не делится на x. Следовательно, xRy не есть отношение эквивалентности.

Задача 12. Является ли отношение из предыдущей задачи отношением порядка?

Решение. Уточним результаты решения предыдущей задачи. Рассматриваемое отношение xRy транзитивно, антирефлексивно (не выполняется xRх) и антисимметрично (если xRy, тоне выполняется yRx). Поэтому xRy – отношение строгого порядка.

Задача 13. Является ли упорядоченным или частично упорядоченным множество М с отношением xRy на нем из задач 8, 9?

Решение. Очевидно, не все пары элементов множества М сравнимы: например, 15 и 24, 10 и 18 и другие. Поэтому М – частично упорядоченное.

Задача 14. Пусть S (x, y, z) – трехместное отношение «x = y•z» на том же множестве М, что и в задаче 8: {4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24}. Сколько троек (x, y, z), элементы которых находятся в отношении S (x, y, z)?

Решение. Все тройки, удовлетворяющие заданным условиям: (16, 4, 4), (20, 4, 5), (20, 5, 4), (24, 4, 6), (24, 6, 4); их число – 5. Заметим, что если y ¹ z, то (x, y, z) и (x, z, y) - разные тройки, но поскольку операция умножения коммутативна, то выполняется эквивалентность S (x, y, z) «

S (x, z, y), т.е. вместе с каждой тройкой S (x, y, z) условию удовлетворяет и тройка S (x, z, y).

Задача 15. Числа 83, 1906, 44, 584, 4225 упорядочить (а) по величине, (б) по алфавиту как слова в алфавите {0, 1,…, 9}, (в) по сумме цифр.

Решение. (а) 44, 83, 584, 1906, 4225;

(б) 1906, 4225, 44, 584, 83;

(в) 44, 83, 4225, 1906, 584.

Сумма цифр: 8 11 13 16 17

 

 

Приложение 2