В действующих документах нормативные значения не совпадают с м.о. и сдвинуты по отношению к среднему значению.
 , (9.1)
, (9.1)
где  – м.о. и коэффициент вариации нормативного значения нагрузки; – м.о. и коэффициент вариации нормативного значения нагрузки;  – то же сопротивления; – то же сопротивления;  – коэффициенты, показывающие какое число стандартов отсчи-тывается от м.о. при назначении нормативных значений нагрузки и сопротивления. – коэффициенты, показывающие какое число стандартов отсчи-тывается от м.о. при назначении нормативных значений нагрузки и сопротивления. |  |
При коэффициенте изменчивости прочности менее 0,06–0,08 применяется нормальный закон распределения (т.е. не учитываются моменты высших порядков – асимметрия и эксцесс). Более всего это относится к стали, для бетона, каменной кладки, древесины и других материалов с коэффициентом изменчивости 0,15–0,25 корректнее использовать более точные законы распределения, учитывающие асимметрию и эксцесс. Например, функция распределения, полученная из распределения Пирсона III типа:
 , (9.2)
, (9.2)
где g и b – параметры, учитывающие асимметрию.
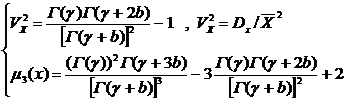 , (9.3)
, (9.3)
асимметрия  . (9.4)
. (9.4)
По СНиП II-23-81 «Стальные конструкции. Нормы проектирования» (приложение 8а, стр. 92) при испытаниях металла нормативное значение предела текучести  или временного сопротивления стали
или временного сопротивления стали  определяется по результатам статистической обработки:
определяется по результатам статистической обработки:
 , (9.5)
, (9.5)
где  – математическое ожидание предела текучести или временного сопротивления;
– математическое ожидание предела текучести или временного сопротивления;  – среднеквадратическое отклонение предела текучести или временного сопротивления.
– среднеквадратическое отклонение предела текучести или временного сопротивления.
 ; (9.6)
; (9.6)
или по (3.8)
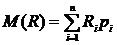 , (9.7)
, (9.7)
где  .
.  появляется один раз;
появляется один раз;  – вероятность появления возможных значений
– вероятность появления возможных значений  предела текучести или временного сопротивления;
предела текучести или временного сопротивления;  – число испытанных образцов (полная группа несовместных событий);
– число испытанных образцов (полная группа несовместных событий); 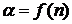 – коэффициент, учитывающий объем выборки.
– коэффициент, учитывающий объем выборки.
 , (9.8)
, (9.8)
при  ;
;
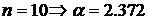 ;
;
 ;
;
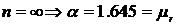 ,
,
 показывает, на какое число стандартов
показывает, на какое число стандартов  сдвинуто нормативное сопротивление по отношению к математическому ожиданию.
сдвинуто нормативное сопротивление по отношению к математическому ожиданию.
Чем больше  , тем достовернее полученные результаты, тем меньше
, тем достовернее полученные результаты, тем меньше  и больше
и больше  (
( или
или  ).
).

 . (9.9)
. (9.9)
При значении коэффициента вари-ации (изменчивости)  >0.1 использовать результаты, полученные из опытов, не допускается, так как они ненадежны. Кроме того, коэффи-циентом надежности по материалу
>0.1 использовать результаты, полученные из опытов, не допускается, так как они ненадежны. Кроме того, коэффи-циентом надежности по материалу  >1 учитывается разброс найденных нормативных сопротивлений (изменчивость в неблагоприятную сторону).
>1 учитывается разброс найденных нормативных сопротивлений (изменчивость в неблагоприятную сторону).
Расчетное сопротивление вычисляется по формулам (здесь – для стальных конструкций):
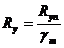 – по пределу текучести;
– по пределу текучести;
или
 – по пределу прочности.
– по пределу прочности.
Нормативные значения принимаются с обеспеченностью 0.95, т.е. вероятность того, что случайное фактическое сопротивление  >
>  равна 0.95, тогда вероятность непревышения:
равна 0.95, тогда вероятность непревышения:

или, приняв нормальное распределение, через интеграл вероятности Гаусса Ф(х):
 .
.
ПРИМЕР 1:
Определим математическое ожидание предела текучести для стали С235. Примем  (худший вариант), и тогда
(худший вариант), и тогда

 МПа при
МПа при  МПа.
МПа.
При изменчивости  МПа.
МПа.
Определим, насколько сдвинуто влево от математического ожидания предела текучести 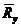 расчетное сопротивление по пределу текучести
расчетное сопротивление по пределу текучести  .
.
 ;
; 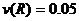 ;
;  МПа;
МПа;  МПа;
МПа;
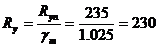 МПа;
МПа;
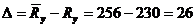 МПа;
МПа;
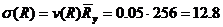 МПа.
МПа.
Таким образом, расчетное сопротивление сдвинуто влево от математического ожидания предела текучести 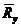 на
на  и вероятность того, что предел текучести будет меньше расчетного сопротивления
и вероятность того, что предел текучести будет меньше расчетного сопротивления 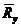 равна:
равна:

Обеспеченность расчетного сопротивления этой стали равна
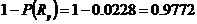 .
.
Нормами строго установлена обеспеченность расчетных сопротивлений только для древесины и древесных пластиков. Она составляет 0,99 и выше. Для бетонов, кирпича и других конструкционных материалов нет единой обеспеченности этой важнейшей прочностной характеристики, используемой при проектировании.
Нужно также учитывать, что в СНиПах приведены округленные значения прочностных и деформационных характеристик. Это в определенной степени влияет на обеспеченность расчетных значений.
ПРИМЕР 2:
Определить обеспеченность расчетного сопротивления изгибу древесно-стружечных плит со следующими характеристиками:
R н = 16 МПа, R = 5,76 МПа, коэффициент вариации v = 0,16, коэффициент длительного сопротивления m дл = 0,53, масштабный коэффициент k p = 0,8.
РЕШЕНИЕ:
Коэффициент надежности по материалу вычислим из соотношения между нормативным и расчетным сопротивлением с учетом того, что масштабный эффект и различие длительной и кратковременной прочности учитываются отдельными коэффициентами, которые будем считать детерминированными.
Из соотношений расчетного и нормативного сопротивлений для древесины и древесных пластиков

отсюда
 =
= 
Выразим нормативное сопротивление через временное с учетом того, что обеспеченность его 0,95:
R н = R ср(1 - 1,645 v)
где коэффициент 1,645 определяет обеспеченность 0,95.
В свою очередь так же можно выразить расчетное сопротивление
R = R ср(1 - tv),
где t определяет неизвестную обеспеченность.
Из этих соотношений

и отсюда

По таблице Ф(t) находим, что такой коэффициент соответствует значению интеграла вероятностей Ф(t) = 0,490.
Тогда вероятность непревышения расчетного сопротивления составляет
0,5 - Ф(t) = 0,50 - 0,49 = 0,01,
что соответствует обеспеченности P = 1 - 0,01 = 0,99.
Именно такое значение обеспеченности приведено для древесных плит в нормах по проектированию деревянных конструкций.
Решим эту же задачу для случая действия только кратковременной нагрузки малой продолжительности, соизмеримой с длительностью стандартных испытаний (например, при сейсмической нагрузке), когда m дл = 1. Тогда
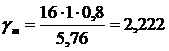

Ф(t) = 0,499985;
0,5 - Ф(t) = 0,000015.
Обеспеченность в этом случае составляет
P = 1 - 0,000015 = 0,999985
Таким образом, при совместном действии длительной и кратковременной (снеговой) нагрузок в течение примерно двух месяцев может разрушиться 1 образец древесных плит из 100, а при кратковременном нагружении до напряжений σ = Rн - только 15 образцов из 1000000 (МИЛЛИОНА) или 1 из 66667.
 2017-12-14
2017-12-14 932
932








