Математическое ожидание и дисперсия являются важными характеристиками случайного процесса, но они не дают достаточного представления о том, какой характер будут иметь отдельные реализации случайного процесса. Это хорошо видно из рис. 19.4, где показаны реализации двух случайных процессов, совершенно различных по своей структуре, хотя и имеющих
одинаковые значения математического ожидания и дисперсии. Штриховыми линиями на рис. 19.4 показаны значения 3σx(t) для случайных процессов.
Процесс, изображенный на рис. 19.4, а, от одного сечения к другому протекает сравнительно плавно, а процесс на рис. 19.4, б обладает сильной изменчивостью от сечения к сечению. Поэтому статистическая связь между сечениями в первом случае больше, чем во втором, однако ни по математическому ожиданию, ни по дисперсии этого установить нельзя.
Чтобы в какой-то мере охарактеризовать внутреннюю структуру случайного процесса, т. е. учесть связь между значениями случайного процесса в различные моменты времени или, иными словами, учесть степень изменчивости случайного процесса, необходимо ввести понятие о корреляционной (автокорреляционной) функции случайного процесса.
Корреляционной функцией случайного процесса X(t) называют неслучайную функцию двух аргументов Rx(t1;t2)которая для каждой пары произвольно выбранных значений аргументов (моментов времени) t1; и t2 равна математическому ожиданию произведения двух случайных величин Ẋ(t1) и Ẋ(t2) соответствующих сечений случайного процесса:
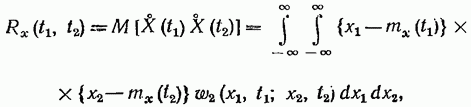 (19.28)
(19.28)
где ω2(x1,t1;x2,t2) — двумерная плотность вероятности;
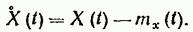 (19.29) центрированный случайный процесс;
(19.29) центрированный случайный процесс;
mx(t) - математическое ожидание (среднее значение) случайного процесса.
Различные случайные процессы в зависимости от того, как изменяются их статистические характеристики с течением времени, делят на стационарные и нестационарные. Разделяют стационарность в узком смысле и стационарность в широком смысле.
Стационарным в узком смысле называют случайный процесс X(t), если его n-мерные функции распределения и плотности вероятности при любом n не зависят от сдвига всех точек t1,t2,…,tn вдоль оси времени на одинаковую величину 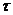 т. е.
т. е.
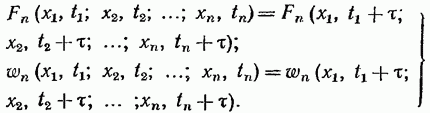 (19.30)
(19.30)
Это означает, что два процесса X(t) и X(t+ 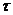 ) имеют одинаковые статистические свойства для любого
) имеют одинаковые статистические свойства для любого 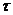 т. е. статистические характеристики стационарного случайного процесса неизменны во времени.
т. е. статистические характеристики стационарного случайного процесса неизменны во времени.
Стационарный случайный процесс — это своего рода аналог установившегося процесса в детерминированных системах. Любой переходный процесс не является стационарным.
Стационарным в широком смысле называют случайный процесс X(t), математическое ожидание которого постоянно:
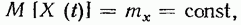 (19.31)
(19.31)
а корреляционная функция зависит только от одной переменной — разности аргументов 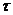 = t2 – t1; при этом корреляционную функцию обозначают
= t2 – t1; при этом корреляционную функцию обозначают
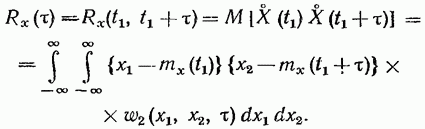 (19.32)
(19.32)
Процессы, стационарные в узком смысле, обязательно стационарны и в широком смысле; однако обратное утверждение, вообще говоря, неверно.
Понятие случайного процесса, стационарного в широком смысле, вводится тогда, когда в качестве статистических характеристик случайного процесса используются только математическое ожидание и корреляционная функция. Часть теории случайных процессов, которая описывает свойства случайного процесса через его математическое ожидание и корреляционную функцию, называют корреляционной теорией.
Для случайного процесса с нормальным законом распределения математическое ожидание и корреляционная функция полностью определяют его n-мерную плотность вероятности.
Поэтому для нормальных случайных процессов понятия стационарности в широком и узком смысле совпадают.
Теория стационарных процессов разработана наиболее полно и позволяет сравнительно просто производить расчеты для многих практических случаев. Поэтому допущение о стационарности иногда целесообразно делать также и для тех случаев, когда случайный процесс хотя и нестационарен, но на рассматриваемом отрезке времени работы системы статистические характеристики сигналов не успевают сколько-нибудь существенно измениться. В дальнейшем, если не будет оговорено особо, будут рассматриваться случайные процессы, стационарные в широком смысле.
При изучении случайных процессов, стационарных в широком смысле, можно ограничиться рассмотрением только процессов с математическим ожиданием (средним значением), равным нулю, т. е. mx(t) = 0, так как случайный процесс с ненулевым математическим ожиданием представляют как сумму процесса с нулевым математическим ожиданием и постоянной неслучайной (регулярной) величиной, равной математическому ожиданию этого процесса.
При mx(t) = 0 выражение для корреляционной функции
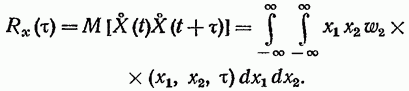 (19.33)
(19.33)
В теории случайных процессов пользуются двумя понятиями средних значений. Первое понятие о среднем значении — это среднее значение по множеству (или математическое ожидание), которое определяется на основе наблюдения над множеством реализаций случайного процесса в один и тот же момент времени. Среднее значение по множеству принято обозначать волнистой чертой над выражением, описывающим случайную функцию:
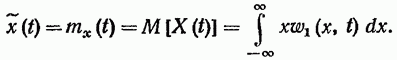 (19.34)
(19.34)
В общем случае среднее значение по множеству является функцией времени t.
Другое понятие о среднем значении — это среднее значение по времени, которое определяется на основе наблюдения за отдельной реализацией случайного процесса x(t) на протяжении достаточно длительного времени Т. Среднее значение по времени обозначают прямой чертой над соответствующим выражением случайной функции и определяют по формуле:
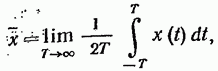 (19.35)
(19.35)
если этот предел существует.
Среднее значение по времени в общем случае различно для отдельных реализаций множества, определяющих случайный процесс. Вообще говоря, для одного и того же случайного процесса среднее по множеству и среднее по времени значения различны. Однако существует класс стационарных случайных процессов, называемых эргодическими, для которых среднее по множеству равно среднему по времени, т. е. 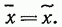
Корреляционная функция Rx(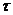 ) эргодического стационарного случайного процесса X(t) неограниченно убывает по модулю при │
) эргодического стационарного случайного процесса X(t) неограниченно убывает по модулю при │ 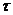 │→∞
│→∞
Однако надо иметь в виду, что не всякий стационарный случайный процесс является эргодическим, например случайный процесс X(t), каждая реализация которого xi(t) постоянна во времени (рис. 19.5), является стационарным, но не эргодическим.

Рис. 19.5
В этом случае средние значения, определенные по одной реализации и в результате обработки множества реализаций, не совпадают. Один и тот же случайный процесс в общем случае может быть эргодическим по отношению к одним статистическим характеристикам и неэргодическим по отношению к другим. В дальнейшем будем считать, что по отношению ко всем статистическим характеристикам условия эргодичности выполняются.
Свойство эргодичности имеет очень большое практическое значение. Для определения статистических свойств некоторых объектов, если трудно осуществить одновременное наблюдение за ними в произвольно выбранный момент времени (например, при наличии одного опытного образца), его можно заменить длительным наблюдением за одним объектом. Иными словами, отдельная реализация эргодического случайного процесса на бесконечном промежутке времени полностью определяет весь случайный процесс с его бесконечными реализациями. Собственно говоря, этот факт лежит в основе описанного ниже метода экспериментального определения корреляционной функции стационарного случайного процесса по одной реализации.
Как видно из определения, корреляционная функция представляет собой среднее значение по множеству. Для эргодических случайных процессов корреляционную функцию Rx можно определить как среднее по времени от произведения [x(t) - 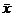 ] и [x(t+
] и [x(t+ 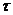 ) -
) - 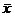 ], т. е.
], т. е.
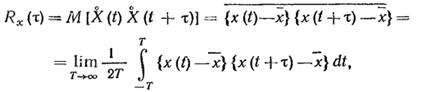 (19.36)
(19.36)
где x(t) — любая реализация случайного процесса; 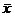 - среднее значение по времени, определяемое по
- среднее значение по времени, определяемое по
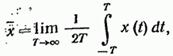 . (19.37)
. (19.37)
Если среднее значение случайного процесса равно нулю 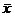 = 0, то
= 0, то
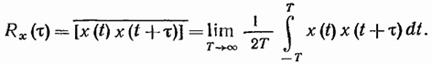 (19.38)
(19.38)
Основываясь на свойстве эргодичности, можно дисперсию Dx определить как среднее по времени от квадрата центрированного случайного процесса, т. е.
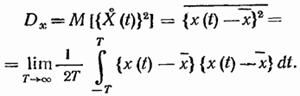 (19.39)
(19.39)
Сравнивая выражения Rx(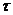 ) и Dx при
) и Dx при 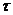 =0, можно установить очень важную связь между дисперсией и корреляционной функцией — дисперсия стационарного случайного процесса равна начальному значению корреляционной функции:
=0, можно установить очень важную связь между дисперсией и корреляционной функцией — дисперсия стационарного случайного процесса равна начальному значению корреляционной функции:
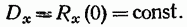 (19.40)
(19.40)
Из этого видно, что дисперсия стационарного случайного процесса постоянна, а следовательно, постоянно и среднее квадратическое отклонение:
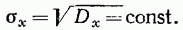 (19.41)
(19.41)
Статистические свойства связи двух случайных процессов X(t) и G(t) можно характеризовать взаимной корреляционной функцией Rxg(t1,t2), которая для каждой пары произвольно выбранных значений аргументов t1 и t2 равна
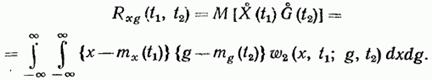 (19.42)
(19.42)
Для эргодических случайных процессов вместо этого можно записать
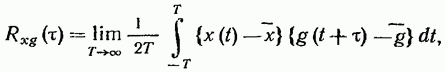 (19.43)
(19.43)
где x(t) и g(t)— любые реализации стационарных случайных процессов X(t) и G(t), соответственно.
Взаимная корреляционная функция Rxg(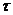 ) характеризует взаимную статистическую связь двух случайных процессов X(t) и G(t) в разные моменты времени, отстоящие друг от друга на промежуток времени
) характеризует взаимную статистическую связь двух случайных процессов X(t) и G(t) в разные моменты времени, отстоящие друг от друга на промежуток времени 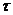 . Значение Rxg(0)характеризует эту связь в один и тот же момент времени.
. Значение Rxg(0)характеризует эту связь в один и тот же момент времени.
Из предыдущего выражения следует, что
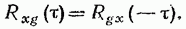 (19.44)
(19.44)
Если случайные процессы X(t) и G(t) статистически не связаны друг с другом и имеют равные нулю средние значения, то их взаимная корреляционная функция для всех  равна нулю. Однако обратный вывод о том, что если взаимная корреляционная функция равна нулю, то процессы независимы, можно сделать лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения), общей же силы обратный закон не имеет.
равна нулю. Однако обратный вывод о том, что если взаимная корреляционная функция равна нулю, то процессы независимы, можно сделать лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения), общей же силы обратный закон не имеет.
Заметим, что корреляционные функции могут вычисляться и для неслучайных (регулярных) функций времени. Однако когда говорят о корреляционной функции Rx( ) регулярной функции x(t), то под этим понимают просто результат формального
) регулярной функции x(t), то под этим понимают просто результат формального
применения к регулярной функции x(t) операции, выражаемой интегралом:
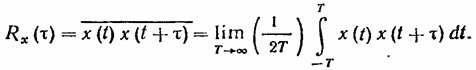 (19.45)
(19.45)
Приведем некоторые основные свойства корреляционных функций Rx(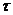 ).
).
1. Начальное значение корреляционной функции равно дисперсии случайного процесса:
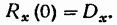 (19.46)
(19.46)
2. Значение корреляционной функции при любом 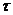 не может превышать ее начального значения, т. е.
не может превышать ее начального значения, т. е.
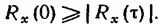 (19.47)
(19.47)
Чтобы доказать это, рассмотрим очевидное неравенство 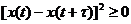 из которого следует
из которого следует 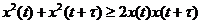 .
.
Находим средние значения по времени от обеих частей последнего неравенства:
 (19.48)
(19.48)
Таким образом, получим неравенство Rx(0) ≥ │Rx(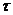 )│.
)│.
3. Корреляционная функция есть четная функция 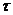 , т. е.
, т. е.
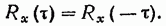 (19.49)
(19.49)
Это вытекает из самого определения корреляционной функции. Действительно,
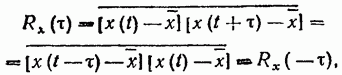 (19.50)
(19.50)
поэтому на графике корреляционная функция всегда симметрична относительно оси ординат.
4. Корреляционная функция суммы случайных процессов
Z(t) = X(t) + G(t) определяется выражением
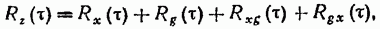 (19.51)
(19.51)
где Rxg( ) и Rgx(
) и Rgx(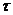 ) — взаимные корреляционные функции
) — взаимные корреляционные функции
Действительно,
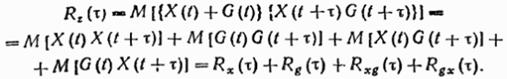 (19.52)
(19.52)
5. Корреляционная функция постоянной величины x(t)= А0 равна квадрату этой постоянной 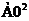 , что вытекает из самого определения корреляционной функции:
, что вытекает из самого определения корреляционной функции:
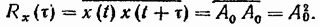 (19.53)
(19.53)
6. Корреляционная функция периодической функции, например  представляет собой косинусоиду, т. е.
представляет собой косинусоиду, т. е.
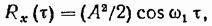 (19.54)
(19.54)
имеющую ту же частоту 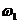 , что и x(t), и не зависящую от сдвига фазы
, что и x(t), и не зависящую от сдвига фазы 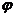 .
.
Чтобы доказать это, заметим, что при нахождении корреляционных функций периодических функций x(t) можно использовать следующее равенство:
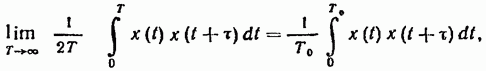 (19.55)
(19.55)
где 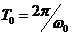 — период функции x(t).
— период функции x(t).
Последнее равенство получается после замены интеграла с пределами от —Т до Т при Т→∞ суммой отдельных интегралов с пределами от (k-1)T0 до kT0,
где k =0, 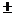 1,
1, 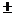 2,…..
2,….. 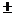 n
n  и использования периодичности подынтегральных функций.
и использования периодичности подынтегральных функций.
Тогда, учитывая сказанное выше, получим т.
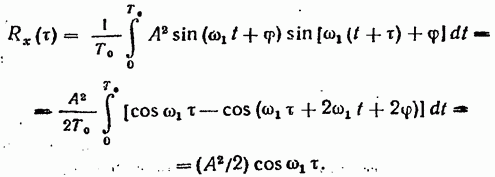 (19.56)
(19.56)
7. Корреляционная функция временной функции, разлагаемой в ряд Фурье:
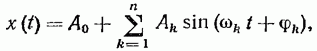 (19.57)
(19.57)
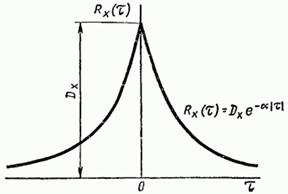
Рис. 19.6.
имеет на основании изложенного выше следующий вид:
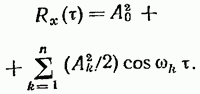 (19.58)
(19.58)
8. Типичная корреляционная функция стационарного случайного процесса имеет вид, представленный на (рис. 19.6). Ее можно аппроксимировать следующим аналитическим выражением:
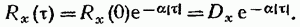 (19.59)
(19.59)
 2017-12-14
2017-12-14 16470
16470
