Стационарные случайные процессы

К числу наиболее простых для изучения случайных процессов относятся стационарные случайные процессы у которых все вероятностные характеристики не зависят от времени. В частности, у стационарного случайного процесса математическое ожидание и дисперсия из функций аргумента t превращаются в константы:

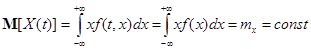, (6.20)

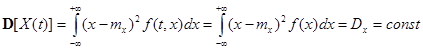. (6.21)

Это означает, что все сечения стационарного случайного процесса имеют одинаковое математическое ожидание и дисперсию (рис.6.4).

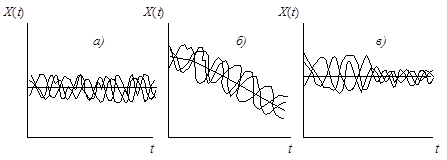
Рис.6.4. Реализации стационарного (а) и нестационарных (б,в) случайных процессов; б – нестационарность по математическому ожиданию; в – нестационарность по дисперсии.

Различают стационарные случайные процессы в узком смысле и в широком смысле.

Случайный процесс называется стационарным в узком смысле, если его n -мерная плотность распределения не изменится при сдвиге всех его временных аргументов на одинаковую произвольную величину q.

Поясним это на примере двумерной плотности распределения. Если стационарный случайный процесс X (t) имеет двумерную плотность f (t ₁, t ₂, x ₁, x ₂), то она не изменится если заменить t ₁ на t ₁ + q, а t ₂на t ₂ +q.

Это означает, что плотность распределения стационарного случайного процесса не зависит от того в какие моменты t ₁ и t ₂ рассматриваются сечения, а зависит от расстояния между этими сечениями t ₁ – t ₂ = t.

Случайный процесс называется стационарным в широком смысле, если его математическое ожидание постоянно (m_x = conct), а корреляционная функция – есть функция сдвига между аргументами: K_x (t ₁, t ₂) = k_x (t).

Если стационарный случайный процесс является стационарным в узком смысле, то он является стационарным и в широком смысле (обратное утверждение не всегда верно).

Корреляционная функция стационарного случайного процесса обладает следующими свойствами:

1. Она является четной функцией своего аргумента

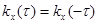. (6.22)

2. Значение корреляционной функции стационарного случайного процесса при нулевом сдвиге t равно дисперсии случайного процесса

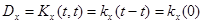. (6.23)

3. 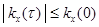. (6.24)

Помимо корреляционной функции используется нормированная корреляционная функция стационарного случайного процесса, которую также называю автокорреляционной функцией:

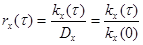. (6.25)

Она обладает практически теми же свойствами, что и корреляционная функция, у которой изменен масштаб по оси ординат:

1. 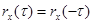. (6.26)

2. 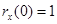. (6.27)

3. 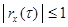. (6.28)