Доверительный интервал для дисперсии при неизвестном математическом ожидании

Найдем доверительный интервал для дисперсии нормально распределенного признака Х с неизвестным математическим ожиданием. При выводе интервальной оценки, в случае известного математического ожидания, мы пользовались величиной 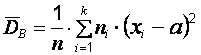. Теперь это значение использовать нельзя, поэтому в качестве несмещенной оценки дисперсии будем использовать исправленную выборочную дисперсию . Случайная величина имеет распределение Пирсона с степенями свободы. Выберем близкую к единице вероятность 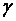и найдем интервал, в который попадает неизвестный параметр с надежностью 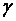. 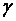Для этого повторим рассуждения предыдущего раздела и получим, что оцениваемое значение дисперсии с надежностью покрывается доверительным интервалом .

Доверительный интервал для среднего