Пусть 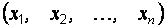 – выборка наблюдений из нормальной генеральной совокупности. Найдем доверительный интервал для дисперсии
– выборка наблюдений из нормальной генеральной совокупности. Найдем доверительный интервал для дисперсии 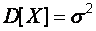 нормально распределенного признака Х с известным математическим ожиданием
нормально распределенного признака Х с известным математическим ожиданием 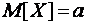 . Поскольку значение математического ожидания известно, то в качестве оценки величины
. Поскольку значение математического ожидания известно, то в качестве оценки величины 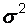 возьмем точечную оценку дисперсии
возьмем точечную оценку дисперсии 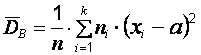 , которую будем рассматривать как случайную величину, зависящую от случайной выборки. Тогда величина
, которую будем рассматривать как случайную величину, зависящую от случайной выборки. Тогда величина 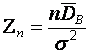 является суммой квадратов значений
является суммой квадратов значений 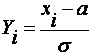 . Эти величины имеют стандартное нормальное распределение с параметрами (0,1), а сумма
. Эти величины имеют стандартное нормальное распределение с параметрами (0,1), а сумма 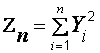 имеет
имеет 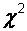 (хи-квадрат) распределение Пирсона с
(хи-квадрат) распределение Пирсона с 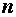 степенями свободы. Плотность случайной величины, распределенной по закону
степенями свободы. Плотность случайной величины, распределенной по закону 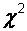 , имеет вид
, имеет вид
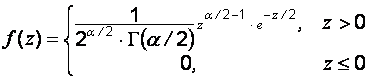 ,
,
где 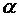 – число степеней свободы. Пользуясь плотностью
– число степеней свободы. Пользуясь плотностью 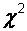 –распределения найдем интервал, в который значения
–распределения найдем интервал, в который значения 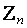 попадают с надежностью
попадают с надежностью 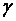 . Обозначим этот интервал
. Обозначим этот интервал 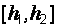 . Поскольку распре-деление
. Поскольку распре-деление 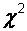 не является симметричным, то чтобы получить симметричный относительно параметра интервал, значения
не является симметричным, то чтобы получить симметричный относительно параметра интервал, значения 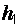 и
и 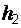 выберем так, чтобы вероятности попадания значений
выберем так, чтобы вероятности попадания значений 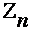 левее
левее 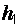 и правее
и правее 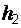 были одинаково равными
были одинаково равными 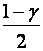 . Тогда
. Тогда 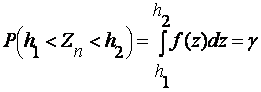 . Числа
. Числа 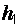 и
и 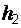 можно отыскать по специальной таблице критических точек распределения
можно отыскать по специальной таблице критических точек распределения 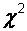 , исходя из того, что
, исходя из того, что 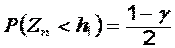 ,
, 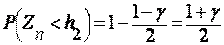 . После того, как числа
. После того, как числа 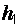 и
и 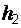 выбраны, возможно определить доверительный интервал для дисперсии
выбраны, возможно определить доверительный интервал для дисперсии 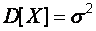 .
.
Так как 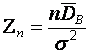 , то неравенство
, то неравенство 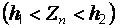 преобразуется к неравенству
преобразуется к неравенству 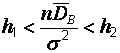 или, в эквивалентном виде,
или, в эквивалентном виде, 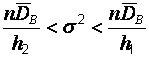 . Это двойное неравенство означает, что доверительным интервалом для
. Это двойное неравенство означает, что доверительным интервалом для 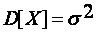 с надежностью
с надежностью 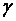 является промежуток
является промежуток 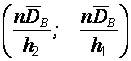 .
.
Замечание. Таблицы критических точек 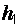 и
и 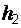 распределения
распределения 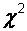 содержат два параметра: уровень значимости
содержат два параметра: уровень значимости 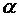 , определяемый значениями
, определяемый значениями 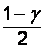 и
и 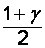 , а также число степеней свободы
, а также число степеней свободы 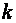 , равное объему выборки
, равное объему выборки 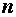 . Критические значения в таблицах чаще всего обозначаются
. Критические значения в таблицах чаще всего обозначаются 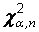 . Приведем для справки команды, с помощью которых можно получить
. Приведем для справки команды, с помощью которых можно получить 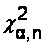 при разных значениях
при разных значениях 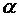 и
и 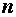 , в таких программах как EXCEL, MATHCAD,MAPLE.
, в таких программах как EXCEL, MATHCAD,MAPLE.
| MAPLE | 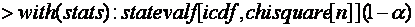 ; ; |
| MATHCAD | 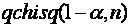 |
| EXCEL | 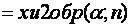 |
 2017-12-14
2017-12-14 1097
1097
