Доверительный интервал для вероятности биномиального распределения

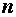Предположим, что проводится серия независимых испытаний, в каждом из которых может появиться событие с одной и той же, но неизвестной нам вероятностью . Причем вероятность появления события в каждом опыте не зависит от исходов других испытаний. Такие испытания называются независимыми относительно данного события . Пусть проведено независимых испытаний. Случайная величина представляет собой число появления события в данной серии испытаний. Возможными значениями этой случайной величины являются целые числа от 0 до 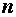. Вероятности этих возможных значений определяются по формуле Бернулли . Закон распределения такой случайной величины называется биномиальным. Математическое ожидание этой случайной величины 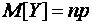, дисперсия .

В реальной ситуации, если проводится серия из 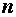независимых испытаний и требуется найти неизвестную вероятность появления события в каждом отдельном испытании, поступают следующим образом. Появлению события в отдельном испытании поставим в соответствие число 1, а если событие не появилось, то поставим в соответствие этому число 0. Тогда можно говорить о случайной величине 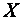, которая принимает два значения: 1 и 0. Любая выборка значений 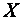состоит из нулей и единиц. Причем число единиц равно количеству появлений события в 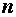опытах.

В качестве точечной оценки неизвестного параметра – вероятности – возьмем частоту появления события в данной серии испытаний: , где – число единиц в случайной выборке . Оценка является несмещенной оценкой параметра .

Найдем доверительный интервал, который покрывает неизвестный параметр с надежностью 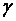. Если оцениваемая вероятность не слишком мала и не слишком велика (0,05 < р < 0,95), то можно считать, что распределение случайной величины близко к нормальному. Этим допущением можно пользоваться, если пр и п (1– р) больше четырех. Выберем при заданной надежности 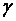числа так, чтобы выполнялись неравенства и . Тогда вероятность попадания значения в интервал будет равна . Для практического нахождения доверительных интервалов с надежностью и при 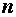от 1 до 30, а также при и 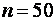можно воспользоваться заранее составленными таблицами, которые можно найти в справочниках по математической статистике.

При больших объемах выборки можно обойтись приближенным построением доверительного интервала. Воспользуемся формулой вероятности отклонения относительной частоты от постоянной вероятности в независимых испытаниях . Обозначим и, с помощью таблицы значений функции Лапласа, решим уравнение . Из полученного значения най-дем .

Тогда , . Чтобы получить доверительный интервал для , нужно выполнить еще ряд преобразований, который мы в данном случае не будем приводить. Заметим только, что при большом объеме выборки малыми слагаемыми можно пренебречь и получить приближенное значение для доверительного интервала в виде .

В.И. Лукашенко

Курс лекций

По дисциплине

«ВЕРОЯТНОСТНЫЕ МЕТОДЫ СТРОИТЕЛЬНОЙ