Пусть по выборке достаточно большого объема, 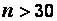 , и при заданной доверительной вероятности
, и при заданной доверительной вероятности 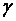 необходимо определить доверительный интервал для математического ожидания
необходимо определить доверительный интервал для математического ожидания 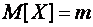 , в качестве оценки которого используется среднее арифметическое (среднее выборочное)
, в качестве оценки которого используется среднее арифметическое (среднее выборочное) 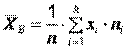 .
.
Закон распределения оценки математического ожидания близок к нормальному (распределение суммы независимых случайных величин с конечной дисперсией асимптотически нормально). Если потребовать абсолютную надежность оценки математического ожидания, то границы доверительного интервала будут бесконечными 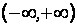 . Выбор любых более узких границ связан с риском ошибки, вероятность которой определяется уровнем значимости
. Выбор любых более узких границ связан с риском ошибки, вероятность которой определяется уровнем значимости 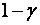 , где значения
, где значения 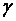 выбираются достаточно близкими к единице, например, 0,9, 0,95, 0,98, 0,99. Величину
выбираются достаточно близкими к единице, например, 0,9, 0,95, 0,98, 0,99. Величину 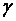 называют надежностью или доверительной вероятностью. Интерес представляет максимальная точность оценки, т.е. наименьшее значение интервала. Для симметричных функций минимальный интервал тоже будет симметричным относительно оценки
называют надежностью или доверительной вероятностью. Интерес представляет максимальная точность оценки, т.е. наименьшее значение интервала. Для симметричных функций минимальный интервал тоже будет симметричным относительно оценки 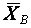 . В этом случае выражение для доверительной вероятности имеет вид
. В этом случае выражение для доверительной вероятности имеет вид 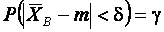 , где
, где 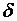 – абсолютная погрешность оценивания.
– абсолютная погрешность оценивания.
Нормальный закон 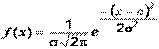 полностью определяется двумя параметрами – математическим ожиданием
полностью определяется двумя параметрами – математическим ожиданием 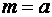 и дисперсией
и дисперсией 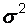 . Величина
. Величина 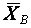 является несмещенной, состоятельной и эффективной оцен-кой математического ожидания, поэтому ее значение принимаем за значе-ние математического ожидания в качестве точечной оценки. Будем пола-гать, что дисперсия
является несмещенной, состоятельной и эффективной оцен-кой математического ожидания, поэтому ее значение принимаем за значе-ние математического ожидания в качестве точечной оценки. Будем пола-гать, что дисперсия 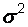 известна, тогда выборочное среднее
известна, тогда выборочное среднее 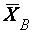 – нор-мально распределенная случайная величина с параметрами
– нор-мально распределенная случайная величина с параметрами 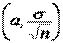 . Для такой случайной величины вероятность попадания на симметричный отно-сительно математического ожидания интервал выражается через функцию Лапласа
. Для такой случайной величины вероятность попадания на симметричный отно-сительно математического ожидания интервал выражается через функцию Лапласа 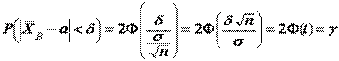 , где
, где 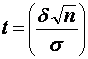 . При заданной надежности
. При заданной надежности 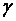 , уравнение
, уравнение 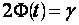 можно решить приближенно с помощью таблицы значений функции Лапласа (приложение, табл. 1). Если точного значения
можно решить приближенно с помощью таблицы значений функции Лапласа (приложение, табл. 1). Если точного значения 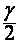 в списке значений нет, то надо найти два бли-жайших к нему значения, одно большее, а другое меньшее, чем
в списке значений нет, то надо найти два бли-жайших к нему значения, одно большее, а другое меньшее, чем 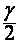 , и найти их среднее арифметическое. Известное значение параметра
, и найти их среднее арифметическое. Известное значение параметра 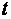 позволяет записать абсолютную погрешность
позволяет записать абсолютную погрешность 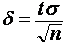 . Теперь можно указать сим-метричный интервал
. Теперь можно указать сим-метричный интервал 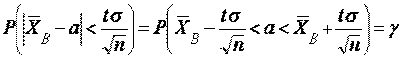 . Полученное соотношение означает, что доверительный интервал
. Полученное соотношение означает, что доверительный интервал 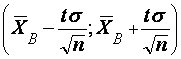 покрывает неизвестный параметр
покрывает неизвестный параметр 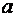 (математическое ожидание) с вероятностью (надежностью)
(математическое ожидание) с вероятностью (надежностью) 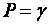 , а точность оценки
, а точность оценки 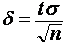 .
.
При фиксированном объеме выборки из оценки 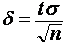 следует, что чем больше доверительная вероятность
следует, что чем больше доверительная вероятность 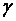 , тем шире границы доверительного интервала (тем больше ошибка в оценке математического ожидания). Чтобы снизить ошибку в оценке значения, можно увеличить объем выборки. При этом, чтобы снизить относительную погрешность на порядок, необходимо увеличить объем выборки на два порядка.
, тем шире границы доверительного интервала (тем больше ошибка в оценке математического ожидания). Чтобы снизить ошибку в оценке значения, можно увеличить объем выборки. При этом, чтобы снизить относительную погрешность на порядок, необходимо увеличить объем выборки на два порядка.
Задача 1. По данным наблюдений случайной величины 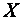 найти доверительный интервал для математического ожидания
найти доверительный интервал для математического ожидания 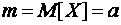 с надежностью
с надежностью 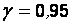 , если известна дисперсия
, если известна дисперсия 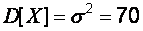 . Выборка представлена таблицей.
. Выборка представлена таблицей.
Таблица 3
Частичные интервалы 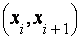
| (10;20) | (20;30) | (30;40) | (40;50) |
| Частоты | ||||
|
Решение задачи 1. Найдем объем выборки, для чего просуммируем указанные в таблице частоты: 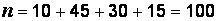 . Среднее выборочное значение вычислим по формуле
. Среднее выборочное значение вычислим по формуле 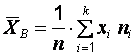 =
= 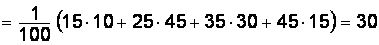 . По заданной надежности
. По заданной надежности
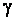 = 0,95 найдем, с помощью таблицы, параметр
= 0,95 найдем, с помощью таблицы, параметр 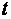 :
: 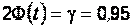 , откуда
, откуда  = 0,475,
= 0,475, 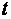 = 1,96. Получим доверительный интервал для математического ожидания
= 1,96. Получим доверительный интервал для математического ожидания 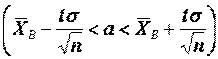
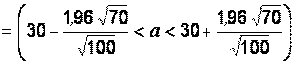 . Проведем вычисления и окончательно запишем, что
. Проведем вычисления и окончательно запишем, что 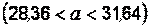 . Таким образом, интервал
. Таким образом, интервал 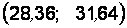 покрывает параметр
покрывает параметр 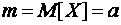 с надежностью
с надежностью 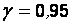 при известной дисперсии
при известной дисперсии 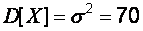 .
.
 2017-12-14
2017-12-14 560
560








