2017-12-14
3662
Во многих случаях предположение о нормальном распределении случайной величины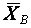 
становится приемлемым при 
и вполне хорошо оправдывается при 
. Оценка 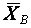вполне пригодна для применения вместо 
. Но не так обстоит дело с дисперсией. Правомочность ее замены на выборочную дисперсию 
не обоснована даже в указанных случаях. При небольшом объеме выборки, 
, закон распределения оценки дисперсии принимать за нормальный неоправданно. Ее распределение следует аппроксимировать распределением хи-квадрат как суммы квадратов центрированных величин (хи-квадрат распределение сходится к нормальному при количестве слагаемых, превышающем 30). Но это утверждение обосновано только тогда, когда случайная величина Х распределена нормально.
Рассмотрим случайные величины 
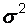(исправленную выборочную дисперсию – несмещенную оценку дисперсии 
) и 
. Тогда случайная величина 
имеет распределение Стьюдента с 
степенями свободы. Функция плотности распределения этой случайной величины имеет вид 
. Распределение Стьюдента симметричное, поэтому полученное соотношение между точностью, надежностью оценки и объемом выборки сохраняется. Выберем число 
так, чтобы выполнялось нера-венство 
. Из определения функции плотности распределения Стьюдента, значения границ интервала для параметра можно записать как решение интегрального уравнения:
|
|
|
Решение этого интегрального уравнения обозначается 
и приводится в статистических таблицах. В данном пособии значения этой величины приведены в приложении, табл. 2. Кроме того, значе-ния при различных 
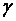и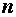 
можно получить, используя программы EXCEL, MATHCAD, MAPLE. Соответствующие команды даны в таблице.
| MAPLE | 
|
| MATHCAD | 
|
| EXCEL | 
|
Приведем неравенство 
к эквивалентному виду 
, или 
. Это неравенство задает доверительный интервал для математического ожидания 
с надежностью :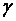
.
Заметим, что полученный доверительный интервал похож на тот, что был получен при условии известной дисперсии: 
. Разница состоит в том, что неизвестное значение 
заменяется во втором случае его выборочной оценкой 
, а числа находятся из распределения Стьюдента, вместо чисел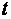 
, которые находятся из нормального распределения. Кроме того, при больших объемах выборки 
можно считать, что, практически, 
, а 
. В этом случае можно пользоваться формулами нормального распределения.
Задача 2. В условиях задачи 1 найти доверительный интервал для математического ожидания с надежностью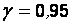 
, если дисперсия неизвестна.
Решение задачи 2. Для удобства вычислений и наглядности еще раз представим таблицу значений.
Частичные интервалы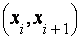 
| (10;20) | (20;30) | (30;40) | (40;50) |
| Частоты | ||||
|
|
|
|
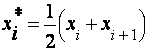Объем выборки составляет 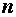= 100. Среднее выборочное значение 
= 30. Вычислим дисперсию 
и исправленную дисперсию 
. Поскольку 
, то 
, а исправленная дисперсия 
= 
, 
. Объем заданной выборки доста-точно большой, 
. Поэтому можно использовать как распределение Стьюдента, так и нормальное распределение. Рассмотрим оба варианта.
Вариант 1 (нормальный закон распределения). Будем полагать, что , а . По заданной надежности 
найдем, с помощью табл. 1 (приложение), параметр :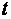 
, откуда 
, 
. Получим доверительный интервал для математического ожида-ния 
.
Проведем вычисления и окончательно запишем, что 
. Таким образом, интервал 
покрывает пара-метр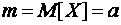 
с надежностью 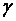= 0,95 при неизвестной дисперсии.
Вариант 2 (закон распределения Стьюдента). По заданной надежности 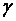= 0,95 найдем, с помощью табл. 2 (приложение), параметр 
: 
. Запишем доверительный интервал для математического ожидания
.
Проведем вычисления и окончательно получим, что 
. Таким образом, интервал 
покрывает пара-метр 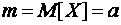с надежностью при неизвестной дисперсии.
Можно заметить, что если значение близко к , то доверительный интервал, полученный с применением закона распределения Стьюдента, будет более широким, чем доверительный интервал, полученный с применением формул нормального распределения, так как 
. Это объясняется тем, что распределение Стьюдента применяется при выборках малых объемов, содержащих недостаточный объем информации.
Задача 3. По данным наблюдений случайной величины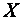 
, распределенной нормально, найти доверительный интервал для математического ожидания 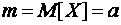с надежностью . Выборка представлена таблицей.
| Частичные интервалы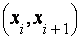
| (5;10) | (10;15) | (15;20) | (20;25) | (25;30) |
| Частоты | |||||
|
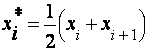| 7,5 | 12,5 | 17,5 | 22,5 | 27,5 |
Решение задачи 3. Найдем объем выборки: 
. Поскольку объем выборки невелик, то применение нормального закона распределения приведет к неоправданному сужению доверительного интервала, поэтому используем формулы, полученные для распределения Стьюдента. Вычислим необходимые параметры:
,
,
,
, 
.
По заданной надежности 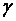= 0,95 найдем, с помощью табл. 2 (приложение), параметр : 
. Доверитель-ный интервал для математического ожидания
или 
. Таким образом, интервал 
покрывает параметр 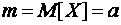с надежностью 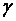= 0,95 при неизвестной дисперсии.
