Методические указания. Рассмотрим пример решения данных задач

Рассмотрим пример решения данных задач.

Задача 1.

Решение.

1. Построим ОДР задачи

 

Строятся граничные прямые.

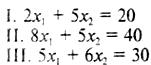
Далее находим пересечение полуплоскостей.

Многоугольник ОАВСD - ОДР задачи.

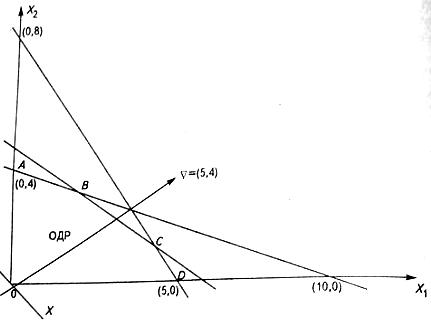
2. Построим вектор-градиент, соединив его вершину (5;4) с началом координат

3. Построим линию уровня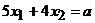

4. При максимизации необходимо перемещать линию уровня в направлении вектора градиента, при минимизации – в противоположном направлении.

С – точка максимума, О – точка минимума.

Определим координаты точки С – пересечение второй и третьей прямой.

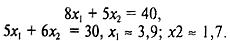
Тогда

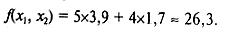
Т.к. координаты точки О(0;0), то минимум целевой функции равен 0.

Задача 2.

Решение.

Приведем задачу к каноническому виду и перейдем к задаче на максимум.

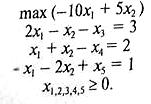
Для нахождения опорного плана переходим к М-задаче.

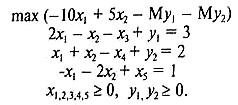
Дальнейшее решение проводим в симплек-таблицах.

 

 

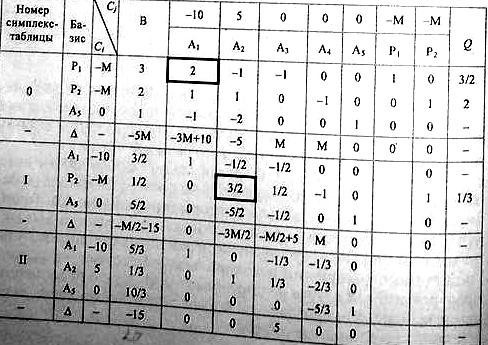
Т.к. все оценки ∆j≥0, то найдено оптимальное решение:

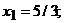
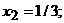
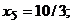
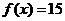(исходная задача на минимум).

 

Задача 3.

Решение.

Правило построения двойственной задачи определяется системой соотношений:

 

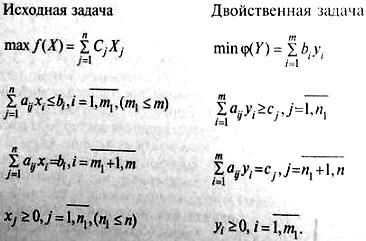
Для использования приведенного выше правила умножим первое неравенство на (-1).

 

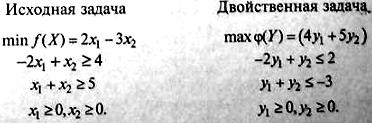
Модуль 2. Пример варианта контрольной работы

 

Задача.

Решить транспортную задачу, заданную матрицей перевозок.

Пункты	В1	В2	В3	Запасы
А1	1	2	3
А2	2	3	3
Потребности				80\60