Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объемом V=1м3, причем желательно израсходовать на его изготовление как можно меньше материала. При постоянной толщине стенок последнее условие означает, что площадь полной поверхности контейнера S должна быть минимальной. Если обозначить через x1,x2, x3 длины ребер контейнера, то задача сведется к минимуму функции
S=2(x1x2 +x2x3 + x1x3).
Эта функция в данном случае является целевой, а условие V=1 ограничением – равенством, которое позволяет исключить один параметр:
V = x1,x2,x3 = 1, x3 = 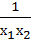 ,S = 2 (х1, х2 +
,S = 2 (х1, х2 + 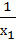 +
+  ).
).
Задача свелась к минимизации функций двух переменных. В результате решения задачи будут значения проектных параметров х1, х2, а затем и х3. В приведенном примере фактически получилась задача безусловной оптимизации для целевой функции, поскольку ограничение – равенство было использовано для исключения параметра х3.
Вместе с тем можно рассматриваемую задачу усложнить и поставить дополнительные условия. Например, потребуем, чтобы данный контейнер имел длину не менее 2м. Это условие будет записано в виде ограничения –неравенства на один из параметров, например
|
|
|
Х1 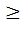 2.
2.
Таким образом, мы получили следующую условную задачу оптимизации: минимизируя функцию и учитывая ограничение – неравенство, найти оптимальное значение параметров плана х1, х2 (х1 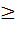 0, х2
0, х2 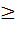 0).
0).
Постановка задачи принятия оптимального решения
1. Формулирование задачи
2. Определение типа
3. Определение множества вариантов и основных критериев для выбора
4. Выбор метода решения задачи
Под принятием решения в исследовании операций понимают сложный процесс, в котором выделяют основные этапы.
1 этап
Построение качественной модели рассматриваемой проблемы, выделение факторов, которые представляются наиболее важными, и установление закономерностей, которым они подчиняются
2этап
Построение математической модели рассматриваемой проблемы – запись в математических терминах качественной модели. Этот этап включает также построение целевой функции переменных – такой числовой характеристики, большему или (меньшему) значению которой соответствует лучшая ситуация с точки зрения принимающего решение.
3этап
Исследование влияния переменных на значение целевой функции. Наэтом этапе находят решение соответствующих экстремальных задач. (Необходимо владение математическим аппаратом для решения математических задач).
4этап
Сопоставление результатов вычислений, полученных на 3 этапе с моделируемым объектом – экспертная проверка результатов (критерий практики) – устанавливается степень адекватности модели и моделируемого объекта в пределах точности исходной информации.
|
|
|
Возможные случаи
1. Случай - когда результаты сопоставления удовлетворительны, то модель принимается. Если речь идет о неоднократном использовании на практике результатов вычислений, возникает задача подготовки модели к эксплуатации.
2. Случай – когда результаты сопоставления не удовлетворительны, то уточняется входная информация о моделируемом объекте, по необходимости уточняется постановка задачи (1этап), уточняется или строится заново математическая модель (2 этап). Решается соответствующая математическая задача (3 этап) и производится сопоставление (4 этап).
Все оптимизационные задачи имеют общую структуру. Их можно классифицировать как задачи минимизации (максимизации) М- векторного показателя эффективностиWm (х), m= 1, 2,…, M, N- мерного аргумента х = (х1, х2, …, хN), компоненты которого удовлетворяют системе ограничений- равенств.
hk(х) = 0, k=1,2, … K, ограничений – неравенств gi(х) 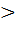 0, j=1,2, …,J
0, j=1,2, …,J
областным ограничениямхIi  хi
хi  хUii = 1,2, … N.
хUii = 1,2, … N.
Все задачи принятия оптимальных решений можно классифицировать в соответствии с видом функции и размерностью Wm (х), hk(х),gi(х) и размерности и созданием вектора х:
Одноцелевое принятие решений Wm (х) скаляр.
Многоцелевое принятие решенийWm (х) вектор.
Принятие решений в условиях определенности.
(исходные данные детерминированные)
Принятие решений в условиях неопределенности.
(Исходные данные случайные).
На практике широко применяют аппарат одноцелевого принятия решений в условиях определенности, который получил название математического программирования. В условиях неопределенности представляет собой стохастическое программирование.
В зависимости от типа экстремума различают методы условной,безусловной,локальной и глобальной оптимизации. Большинство методов относятся кметодам безусловной оптимизации. Исключение составляют немногие методы,
специально разработаные для поиска при наличии ограничений. Из сказанного, однако, не следует делать вывод о неприменимости методов безусловнойоптимизации к большинству экстремальных задач технического проектирования,
где имеют место условные экстремумы. Дело в том, что существует и широкоиспользуются приемы сведения задач условной оптимизациикбезусловной.
Подавляющее большинство методов оптимизации ориентировано на поисклокальных экстремумов. Глобальная оптимизация несравненно сложнеектомуже существующие методы глобальной оптимизации весьма трудоемки и не дают
стопроцентной гарантии определения глобального экстремума.
Характеристика экстремальных задач в проектировании и управлении: многокритериальность, многопараметричность, алгоритмическая форма моделей.
Разработка (или выбор) структуры объекта есть проектная процедура, называемая структурным синтезом, а расчет или выбор значений параметров элементов Х – процедура параметрического синтеза. Задача структурного синтеза формулируется в системотехнике как задача принятия решений (ЗПР). Ее суть заключается в определении цели, множества возможных решений и ограничивающих условий. Классификация ЗПР осуществляется по ряду признаков. По числу критериев различают задачи одно и многокритериальные. По степени неопределенности различают ЗПР детерминированные, ЗПР в условиях риска (при наличии в формулировке задачи случайных параметров), ЗПР в условиях неопределенности, т. е. принеполноте или недостоверности исходной информации. Реальные задачи проектирования являются, как правило, многокритериальными. Одна из основных проблем постановки многокритериальных задач, установление правил предпочтения вариантов. Методами оптимизации многокритериальные задачи сводятся к однокритериальным. Наличие случайных факторов усложняет решение ЗПР. Основные подходы к решению ЗПР в условиях риска заключаются или в решении «для наихудшего случая», или в учете целевой функции математического ожидания и дисперсии выходных параметров. В первом случае задачу решают как детерминированную при завышенных требованиях к качеству решения. Что является главным недостатком подхода. Во втором случае достоверность результатов намного выше, но возникают трудности с оценкой целевой функции. Применение метода Монте-Карло в случае алгоритмических моделей становится единственной альтернативой и, следовательно, для решения требуются значительные вычислительные ресурсы. Задачу параметрического синтеза называют параметрической оптимизацией (или оптимизацией), если ее решают как задачу программирования, т.е. extrF(X), Х 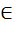 Dx, где F(Х)-целевая функция; Х- вектор управляемых (называемых также проектными или варьируемыми) параметров;Dx= { X
Dx, где F(Х)-целевая функция; Х- вектор управляемых (называемых также проектными или варьируемыми) параметров;Dx= { X  ϕ(Х)
ϕ(Х)  0, ψ(Х) =0} – допустимая область в пространстве управляемых параметров; ϕ(Х) и ψ(Х) – функции –ограничения.Данная запись интерпретируется как задача поиска экстремума целевой функции путем варьирования управляемых параметров в пределах допустимой области. Таким образом, для выполнения расчета номинальных значений параметров необходимо: 1. Сформулировать задачу. 2. Решить задачу поиска экстремума F(Х). Сложность постановки оптимизационных проектных задач обусловлена наличием у проектируемых объектов нескольких выходных параметров, которые могут быть критериями оптимальности.
0, ψ(Х) =0} – допустимая область в пространстве управляемых параметров; ϕ(Х) и ψ(Х) – функции –ограничения.Данная запись интерпретируется как задача поиска экстремума целевой функции путем варьирования управляемых параметров в пределах допустимой области. Таким образом, для выполнения расчета номинальных значений параметров необходимо: 1. Сформулировать задачу. 2. Решить задачу поиска экстремума F(Х). Сложность постановки оптимизационных проектных задач обусловлена наличием у проектируемых объектов нескольких выходных параметров, которые могут быть критериями оптимальности.
|
|
|
Рассмотрим несколько способов выбора критерия оптимальности.
В частном критерии среди выходных параметров один выбирают в качестве целевой функции, а условия работоспособности остальных выходных параметров относят к ограничениям задачи extrF(Х), Х 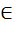 Dx. Эта постановка вполне приемлема, если действительно можно выделить один наиболее критичный выходной параметр. Но вбольшинстве случаев сказывается недостаток частного критерия.
Dx. Эта постановка вполне приемлема, если действительно можно выделить один наиболее критичный выходной параметр. Но вбольшинстве случаев сказывается недостаток частного критерия.
|
|
|
Пример. Электронный усилитель: управляемые параметры Х= (параметры резисторов, конденсаторов, транзисторов), выходные параметры Y= (fв и fн– верхняя и нижняя граничные частоты полосы пропускания; К – коэффициент усиления на средних частотах; Rвх.- входное сопротивление). В качестве целевой функции F(Х) можно выбрать параметр fв, а условия работоспособности остальных выходных параметров отнести к функциям- ограничениям. При исследовании способов выбора критерия оптимальности частный критерий, аддитивный критерий, мультипликативный критерий имеют субъективный характер. Более предпочтительным является максиминный критерий, в качестве целевой функции которого принимают выходной параметр, наиболее неблагополучный с позиций выполнения условий работоспособности. Для оценки степени выполнения условия работоспособности J-го выходного параметра вводят запас работоспособности этого параметра SJи этот запас можно рассматривать как нормированный J-й выходной параметр. Тогда целевая функция вмаксимином критерии есть
F(X)= minSJ(x). J 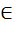 [1:m]- множество целых чисел в диапазоне от 1 до m. Задача поиска экстремума конкретизируется следующим образом. F(X) = maxminSJ (X), X
[1:m]- множество целых чисел в диапазоне от 1 до m. Задача поиска экстремума конкретизируется следующим образом. F(X) = maxminSJ (X), X 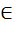 Dx, J
Dx, J 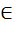 [1: m]. Где допустимая область Dxопределяется только прямыми ограничениями на управляемые параметры Xi:Ximin
[1: m]. Где допустимая область Dxопределяется только прямыми ограничениями на управляемые параметры Xi:Ximin  Xi
Xi  Ximax.
Ximax.
| , |
О
Лекция 2
Методы одномерной безусловной оптимизации
Постановка задачи безусловной оптимизации
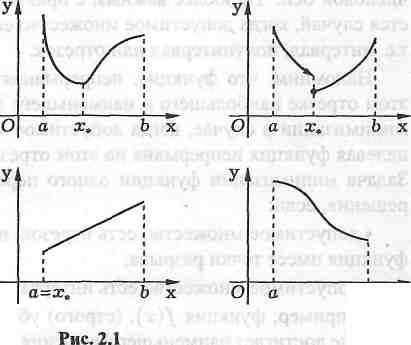
Найти наименьшее (или наибольшее) значение целевой функции y=f(x),заданной на множестве 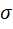 , и определить значение проектного параметра х
, и определить значение проектного параметра х 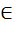 𝞼, при котором целевая функция принимает экстремальное значение. Существование решения поставленной задачи вытекает из теоремы Вейерштрасса. Теорема Вейерштрасса Всякая функция f(x), непрерывная на отрезке [а,
𝞼, при котором целевая функция принимает экстремальное значение. Существование решения поставленной задачи вытекает из теоремы Вейерштрасса. Теорема Вейерштрасса Всякая функция f(x), непрерывная на отрезке [а,  , принимает на этом отрезке наименьшее или наибольшее значение, т. е. на отрезке [а,
, принимает на этом отрезке наименьшее или наибольшее значение, т. е. на отрезке [а,  существуют такие точки х1 и х2 что для любого х
существуют такие точки х1 и х2 что для любого х 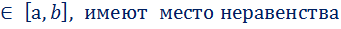
f(x1)  f(x)
f(x)  f(x2). Эта теорема не доказывает единственности решения. Не исключена возможность, когда равные экстремальные значения достигаются сразу в нескольких точках данного отрезка. В частности, такая ситуация имеет место для периодической функции, рассматриваемой на отрезке, содержащей несколько периодов. Рассмотрим методы оптимизации для разных классов целевых функций. Простейший из них - случайдифференцируемой функции f(х) на отрезке [а,
f(x2). Эта теорема не доказывает единственности решения. Не исключена возможность, когда равные экстремальные значения достигаются сразу в нескольких точках данного отрезка. В частности, такая ситуация имеет место для периодической функции, рассматриваемой на отрезке, содержащей несколько периодов. Рассмотрим методы оптимизации для разных классов целевых функций. Простейший из них - случайдифференцируемой функции f(х) на отрезке [а,  ,причем функция задана в виде аналитической зависимости y=f(x), и может быть найдено явное выражение для ее производной f’(x). Нахождение экстремумов таких функций можно проводить известными из курса высшей математики методами дифференциального исчисления.
,причем функция задана в виде аналитической зависимости y=f(x), и может быть найдено явное выражение для ее производной f’(x). Нахождение экстремумов таких функций можно проводить известными из курса высшей математики методами дифференциального исчисления.
Функцияf(х) может достигать своего наименьшего и наибольшего значения либо в граничных точках отрезка [a,  , либо в точках минимума и максимума. Последние точки обязательно должны быть критическими, т.е. производная f’(x) в этих точках обращается в нуль, - это необходимое условие экстремума. Следовательно,для определения наименьшего или наибольшего значения функции f(х) на отрезке [a,b] нужно вычислить ее значения во всех критических точках данного отрезка и в его граничных точках и сравнить полученные значения; наименьшее или наибольшее из них и будет искомым значением. Рассмотрим пример: Найти наименьшее или наибольшее значение функции f(х)=
, либо в точках минимума и максимума. Последние точки обязательно должны быть критическими, т.е. производная f’(x) в этих точках обращается в нуль, - это необходимое условие экстремума. Следовательно,для определения наименьшего или наибольшего значения функции f(х) на отрезке [a,b] нужно вычислить ее значения во всех критических точках данного отрезка и в его граничных точках и сравнить полученные значения; наименьшее или наибольшее из них и будет искомым значением. Рассмотрим пример: Найти наименьшее или наибольшее значение функции f(х)= 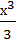 - х2на отрезке [1, 3] Решение: Вычислим производную этой функции: f’(х) = x2 -2х. Приравнивая ее к нулю, найдем критические точки: x2 -2х = 0, х1 = 0, х2 = 2. Точка х = 0 лежит вне рассматриваемого отрезка, поэтому для анализа оставляем три точки: a =1, x2 = 2, b = 3. Вычисляем значения функции в этих точках: f(1) = -
- х2на отрезке [1, 3] Решение: Вычислим производную этой функции: f’(х) = x2 -2х. Приравнивая ее к нулю, найдем критические точки: x2 -2х = 0, х1 = 0, х2 = 2. Точка х = 0 лежит вне рассматриваемого отрезка, поэтому для анализа оставляем три точки: a =1, x2 = 2, b = 3. Вычисляем значения функции в этих точках: f(1) = -  , f(2) = -
, f(2) = -  , f(3) = 0.
, f(3) = 0.
Сравнивая полученные величины, находим, что наименьшего значения функция f(x) достигает в точке x =2, наибольшего в точке
x =3, т. е. fmin = f(2) = -  , fmax = f(3) = 0.
, fmax = f(3) = 0.
В рассмотренном примере уравнение f’(x) = 0 для отыскания критических точек удалось решить непосредственно. Для более сложных видов производной функции f’(x) необходимо использовать численные методы решения нелинейных уравнений. Используемый здесь метод основан на вычислении производной целевой функции требующей ее аналитического представления. В других случаях, когда целевая функция задана в табличном виде или может быть вычислена при некоторых дискретных значениях аргумента, используются различные методы поиска. Они основаны на вычислении целевой функции в отдельных точках и выборе среди них наибольшего или наименьшего значения. Существует ряд алгоритмов решения данной задачи. Рассмотрим некоторые из них.
Методы поиска
Численные методы поиска экстремальных значений функции рассмотрим на примере нахождения минимума функции f(x) на отрезке [a,b]. Будем предполагать, что целевая функция унимодальна, т.е. на данном отрезке она имеет только один минимум. Отметим, что в инженерной практике обычно встречаются именно такие целевые функции. Процесс решения задачи методом поиска состоит в последовательном сужении интервала изменения проектного параметра, называемого интервалом неопределенности. В начале процесса оптимизации его длина равна b - a, а к концу она должна стать менее заданного допустимого значения𝞮 т.е. оптимальное значение проектного параметра должно находиться в интервале неопределенности – отрезке [xn,xn+1], причем xn+1 – xn  𝞮. Наиболее простым способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Пусть n- число элементарных отрезков, h=
𝞮. Наиболее простым способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Пусть n- число элементарных отрезков, h=  - шаг разбиения. Вычислим значения целевой функции yk = fk(x) в узлах xk = a+ kx
- шаг разбиения. Вычислим значения целевой функции yk = fk(x) в узлах xk = a+ kx
(k = 0,1, …, n). Сравнивая полученные значения f (xk), найдем среди них наименьшееyi = f(xi). Число mn = yiможно приближенно принять за наименьшее значение целевой функции f(x) на отрезке [a,b]. Очевидно, что близость mn к минимуму mзависит отчисла точек, и для непрерывной функции f(x)
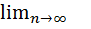 mn =m. т.е. cувеличением числа точек разбиения погрешность в определении минимума стремиться к нулю. В данном методе, который возможно назвать методом перебора основная трудность состоит в выборе nи оценке погрешности. Можно, например, провести оптимизацию с разными шагами и исследовать сходимость такого итерационного процесса. Но это трудоемкий путь. Более экономичным способом уточнения оптимального параметра является использование свойства унимодальности целевой функции, которое позволяет построить процесс сужения интервала неопределенности. Пусть среди всех значений унимодальной функции y= f(x), вычисленных в узлах xk (k= 0, 1, …, n), наименьшим оказалось yi. Это означает, что[xi-1, xi-1], т.е. интервал неопределенности сузился до длины двух шагов.
mn =m. т.е. cувеличением числа точек разбиения погрешность в определении минимума стремиться к нулю. В данном методе, который возможно назвать методом перебора основная трудность состоит в выборе nи оценке погрешности. Можно, например, провести оптимизацию с разными шагами и исследовать сходимость такого итерационного процесса. Но это трудоемкий путь. Более экономичным способом уточнения оптимального параметра является использование свойства унимодальности целевой функции, которое позволяет построить процесс сужения интервала неопределенности. Пусть среди всех значений унимодальной функции y= f(x), вычисленных в узлах xk (k= 0, 1, …, n), наименьшим оказалось yi. Это означает, что[xi-1, xi-1], т.е. интервал неопределенности сузился до длины двух шагов.
y
ax1 …xi-1xixi+1…xn-1 bx
Если размер интервала недостаточен для удовлетворения заданной погрешности, т.е. xi+1 – xi-1 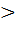 𝞮, то его снова можно уменьшить путем нового разбиения. Получится интервал, равный двум длинам нового шага разбиения. Процесс оптимизации продолжается до достижения заданного размера интервала неопределенности. В данном методе общего поиска можно с помощью некоторой изобретательности, а также разумного выбора шага разбиения добиться эффективного поиска. Например, пусть начальная длина интервала неопределенности равна b – a = 1. Нужно добиться его уменьшения в 100 раз. Этого легко достичь разбиением интервала на 200 частей. Вычислив значения целевой функции f(x), при (k = 0, 1, …., 200), найдем ее минимальное значение f(xi). Тогда искомый интервал неопределенности будетотрезок
𝞮, то его снова можно уменьшить путем нового разбиения. Получится интервал, равный двум длинам нового шага разбиения. Процесс оптимизации продолжается до достижения заданного размера интервала неопределенности. В данном методе общего поиска можно с помощью некоторой изобретательности, а также разумного выбора шага разбиения добиться эффективного поиска. Например, пусть начальная длина интервала неопределенности равна b – a = 1. Нужно добиться его уменьшения в 100 раз. Этого легко достичь разбиением интервала на 200 частей. Вычислив значения целевой функции f(x), при (k = 0, 1, …., 200), найдем ее минимальное значение f(xi). Тогда искомый интервал неопределенности будетотрезок
[xi-1, xi+1]. Однако можно поступить и иначе. Сначала разобьем отрезок на 20 частей и найдем интервал неопределенности длиной 0,1, при этом мы вычислим значения елевой функции в точках xk = a +0,05k (k=0, 1,…,20). Теперь отрезок [xi-1, …xi+1] снова разобьем на 20 частей; получим искомый интервал длиной 0.01, причем значения елевой функции вычисляем в точкахxk= xi-1 + 0.005k (k = 1, 2, …, 19) в точках xi-1 и xi+1значения f(x) уже найдены. Таким образом, в процессе оптимизации произведено 40 вычислений значений целевой функции против 201 в первом случае, т.е. способ разбиения позволяет получить существенную экономию вычисления. Существует ряд специальных методов поиска оптимальных решений с разными способами выбора узлов и сужения интервала неопределенности: метод деления отрезка пополам, метод золотого сечения и другие методы.
Метод золотого сечения.
При построении процесса оптимизации стараются сократить объем вычисления и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f(x). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения. Он состоит в построении последовательности отрезков [a0,b0], [a1,b1], …, стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление значения функции f(x) проводится только лишь один раз. Эта точка называемая золотым сечением выбирается специальным образом. Идею метода хорошо пояснить геометрически.
a0x1x2b0 a=a0 x3 x1 b1 = x2
f(x1) f(x2) (a)f(x3)f(x1) (б)
На первом шаге процессa оптимизации внутри отрезка [a0b0]выбираем две внутренние точки x1или x2. Поскольку в данном случае f(x1)  f(x2), очевидно, что минимум расположен на одном из прилегающих к x1отрезков [a0, x1] или [x1, x2]. Поэтому отрезок [x2, b0] можно отбросить, сузив тем самым первоначальный интервал неопределенности.Второй шаг проводим на отрезке [a1,b] где a1 = a0 , b1 = x2. Нужно снова выбрать две внутренние точки, но одна из них (x1) осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку x3,вычислить значение в f(x3) и провести сравнение. Поскольку здесь f(x3)
f(x2), очевидно, что минимум расположен на одном из прилегающих к x1отрезков [a0, x1] или [x1, x2]. Поэтому отрезок [x2, b0] можно отбросить, сузив тем самым первоначальный интервал неопределенности.Второй шаг проводим на отрезке [a1,b] где a1 = a0 , b1 = x2. Нужно снова выбрать две внутренние точки, но одна из них (x1) осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку x3,вычислить значение в f(x3) и провести сравнение. Поскольку здесь f(x3) 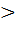 f(x1), ясно что минимум находится на отрезке (x3,b1). Обозначим этот отрезок [a2,b2],снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка [an, bn] не станет меньше заданной величины
f(x1), ясно что минимум находится на отрезке (x3,b1). Обозначим этот отрезок [a2,b2],снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка [an, bn] не станет меньше заданной величины  Теперь рассмотрим способ размещения внутренних точек на каждом отрезке [akbk]. Пусть длина интервала неопределенности равна l, а точка деления делит его на части l1, l2:l1
Теперь рассмотрим способ размещения внутренних точек на каждом отрезке [akbk]. Пусть длина интервала неопределенности равна l, а точка деления делит его на части l1, l2:l1 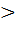 l2l = l1 +l2. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка.
l2l = l1 +l2. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка.
 =
= 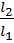 .
.
Из этого соотношения можно найти точку деления, определив отношение l2 / l1. Преобразуем выражение и найдем это значение:
l12= l2l, l12 = l2 (l1 + l2).
l22 +l1l2 - l12 = 0.
(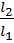 ) +
) + 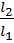 - 1 = 0.
- 1 = 0.
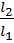 =
= 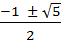 . Поскольку нас интересует только положительное решение, то
. Поскольку нас интересует только положительное решение, то
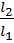 =
=  =
= 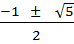
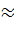 0. 618. Отсюда
0. 618. Отсюда
l1 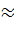 0.618ll2
0.618ll2 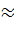 0.382l. Поскольку заранее неизвестно, в какой последовательности (l1и l2 или l2и l1) делить интервал неопределенности, то рассматривают точки, соответствующие двум этим способам деления. На рассмотренном рисунке (а) точки деления x1и x2 выбираются с учетом полученных значений для частей отрезка. В данном случае имеем
0.382l. Поскольку заранее неизвестно, в какой последовательности (l1и l2 или l2и l1) делить интервал неопределенности, то рассматривают точки, соответствующие двум этим способам деления. На рассмотренном рисунке (а) точки деления x1и x2 выбираются с учетом полученных значений для частей отрезка. В данном случае имеем
x1 - a0 = b0 – x2 = 0.382d0
b0 -x1 = x2 - a0 = 0.618d0
d0 =b0 - a0
После первого шага оптимизации получается новый интервал a
Можно показать, что точка x1 делит этот отрезок в требуемом отношении, при этом
b1 - x1 = 0.382d, d1 = b1 - a1.
Для этого проведем очевидные преобразования:
b1 - x1 = x2 - x1 = (b0 - a0) - (x1 – a0) – (b0 – x2) = d0 – 0.382d0 -
- 0.382d0 = 0.236d0`. d1= x2 - a0 = 0.618d0.
Вторая точка деления x3выбирается на том же расстоянии от левой границы отрезка, т.е. x3 – a1 = 0.382d.
И снова интервал неопределенности уменьшается до размера
d2= b2 – a2 = b1 – x3 = 0.618d1 = 0.6182d0
Используя полученные соотношения, можно записать координаты точек деления yи zотрезка [ak,bk] на k + 1 шаге оптимизации (y  z)
z)
Y = 0.618ak + 0.382bk. z = 0.382ak + 0.618bk.
При этом длина интервала неопределенности равна
dk = bk -ak = 0.618kd0
Процесс оптимизации заканчивается при выполнении условии
dk 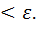 При этом проектный параметр оптимизации составляет
При этом проектный параметр оптимизации составляет
ak  x
x  bk.Можно в качестве оптимального значения принять
bk.Можно в качестве оптимального значения принять
x = ak(или x = bk, или x = 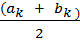 .
.
| начало |

Y=0.618a+0.382b
a 
|
| b=z |
| a=y |
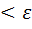 b-a
b-a 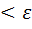
данетнетда
| X=(a+b)/2 |
| конец |
Пример: для оценки сопротивления дороги движению автомобиля при скорости vкм/ч можно использовать эмпирическую формулу
f(v) = 24 -  v +
v +  v2 (для шоссе). Определить скорость, при которой сопротивление будет минимальным.
v2 (для шоссе). Определить скорость, при которой сопротивление будет минимальным.
Решение. Это простейшая задача одномерной оптимизации. Здесь скорость f(v) – целевая функция, скорость vпроектный параметр. Данную задачу легко решит путем нахождения минимума с помощью вычисления производной, поскольку f(v) функция дифференцируемая. Действительно,
F(v) = -  +
+ 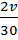 = 0, v = 10 км/ч.
= 0, v = 10 км/ч.
На этой простейшей задаче можно проиллюстрировать метод золотого сечения. Первоначально границы интервала неопределенности примем равными a = 5, b = 20. Результаты вычислений представим в виде таблицы. Расчеты проводятся с погрешностью 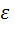 = 1 км/ч.
= 1 км/ч.
| Шаг | a | y | z | b | A | B | b-a |
| 10.7 | 14.3 | 20.7 | 21.3 | ||||
| 8.6 | 10.7 | 14.3 | 20.73 | 20.68 | 9.3 | ||
| 8.6 | 10.7 | 12.1 | 14.3 | 20.68 | 20.61 | 5.7 | |
| 8.6 | 9.9 | 10.7 | 12.1 | 20.66 | 20.68 | 3.5 | |
| 8.6 | 9.4 | 9.9 | 10.7 | 20.68 | 20.66 | 2.1 | |
| 9.4 | 10.7 | 1.3 |
Решение для первого этапа:
Y = 0.618 * 5 + 0.382 * 20 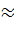 10.7.
10.7.
Z = 0.382* 5 + 0.618 * 20 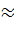 14.3
14.3
A = 24 -  * 10.7 +
* 10.7 +  * 10.72
* 10.72  20.7
20.7
B = 24 -  * 14.32
* 14.32 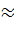 21.3.
21.3.
А  B.
B.
При данной невысокой точности вычислений достаточно четырех шагов оптимизации. В этом случае искомое значение скорости равноv= 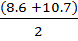 = 9.65 км/ч. После пяти шагов этот результат получается с меньшей погрешностью.
= 9.65 км/ч. После пяти шагов этот результат получается с меньшей погрешностью.
V =  км/ч
км/ч
Метод дихотомии
В последовательности вложенных отрезков, построенных с помощью, исключения отрезка с симметричным выбором внутренних точек, длина очередного отрезка превышает половину kпри котором точки dkи ckна очередном отрезке [ak, bk] расположены максимально близко к середине этого отрезка. Этот способ положен в основу одного из распространенных методов последовательного поиска, называемого методом дихотомии или метода деления пополам. В методе дихотомии используют в качестве параметра достаточно малое число 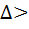 0 (это число должно быть меньше точности вычисления точки минимума). На k- м шаге вычислений на отрезке [ak,bk] выбирают такие точки что ck =
0 (это число должно быть меньше точности вычисления точки минимума). На k- м шаге вычислений на отрезке [ak,bk] выбирают такие точки что ck = 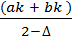 и dk =
и dk = 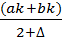 , отстоящие от середины
, отстоящие от середины 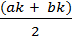 отрезка [ak, bk] на расстоянии
отрезка [ak, bk] на расстоянии 
у 2 
lk+1l k
0 akckdkbkх
Полагаяlk = bk - ak. k  из очевидных геометрических соображений получаем формулу 2lk+1 - 2
из очевидных геометрических соображений получаем формулу 2lk+1 - 2  = lk, k
= lk, k 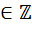 , связывающие длины двух последовательных интервалов неопределенности. Из этой формулы находим lk+1 - 2
, связывающие длины двух последовательных интервалов неопределенности. Из этой формулы находим lk+1 - 2  =
=  откуда получаем следующую зависимость lk - 2
откуда получаем следующую зависимость lk - 2  =
=  . Из этого равенства выводим следующую формулу длины интервала неопределенности получаемого на k-м шаге метода дихотомии:lk =
. Из этого равенства выводим следующую формулу длины интервала неопределенности получаемого на k-м шаге метода дихотомии:lk = 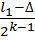 + 2
+ 2 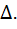 Из данного равенства следует, что lk
Из данного равенства следует, что lk 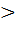 2
2 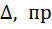 ичемlk
ичемlk  2
2  при k
при k  ассматривая величину lkкак удвоенную точность приближенного решения задачи минимизации, полученную на k-м шаге (при выборе в качестве приближения середины интервала неопределенности), делаем вывод, что параметр
ассматривая величину lkкак удвоенную точность приближенного решения задачи минимизации, полученную на k-м шаге (при выборе в качестве приближения середины интервала неопределенности), делаем вывод, что параметр  дает оценку снизу погрешности приближения в методе дихотомии. В этой ситуации естественное желание выбирать как можно меньшим параметр
дает оценку снизу погрешности приближения в методе дихотомии. В этой ситуации естественное желание выбирать как можно меньшим параметр  . Однако на самом деле его нельзя уменьшать неограниченно. Дело в том, что значения функции, как правило, вычисляются приближенно. При очень малом параметре
. Однако на самом деле его нельзя уменьшать неограниченно. Дело в том, что значения функции, как правило, вычисляются приближенно. При очень малом параметре  точки dk и ckна отрезке [ak, bk] будут расположены настолько близко друг к другу, что не удастся достоверно выяснить, какое из значений функции является большим: различия в значениях функции будет покрываться погрешностью вычислений.
точки dk и ckна отрезке [ak, bk] будут расположены настолько близко друг к другу, что не удастся достоверно выяснить, какое из значений функции является большим: различия в значениях функции будет покрываться погрешностью вычислений.
Методы полиномиальной аппроксимации
Наименьшее значение функции одного переменного можно искать, заменяя функцию приближенно (аппроксимируя) некоторым многочленом. В этом заключается суть совокупности методов, называемых методами полиномиальной аппроксимации. Различаются эти методы степенью аппроксимирующего многочлена и способами вычисления его коэффициентов. При построении аппроксимирующего многочлена могут использоваться не только значения самой функции, но и ее производных.
Метод квадратичной аппроксимации
В этом методе аппроксимирующий многочлен второй степени определяется по трем известным значениям f1, f2, f3минимизируемой функции в трех точках x1, x2,x3. Чтобы определить коэффициенты a, b, cмногочлена второй степени ax2 + bx + c, который в трех различных точках x1, x2, x3принимает заданные значения f1, f2, f3, нужно найти решение системы линейных уравнений axi2 + bxi + c = fi. I = 1,2,3.
Определитель этой системы.
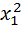 x11
x11
 1 = (x1 – x2) (x1 – x3) (x2-x3).
1 = (x1 – x2) (x1 – x3) (x2-x3).
 x3 1
x3 1
Представляет собой определитель Вандермонда и отличен от нуля, когда x1, x2, x3 попарно различны. В этом случае система линейных уравнений имеет решение, и притом единственное.Находятся выражения для коэффициентов a, b, c.Подставляются выражения для коэффициентов a, b в необходимое условие y’= 2ax + b = 0 экстремума функции и вычисляется единственная стационарная точка аппроксимирующего многочлена.Существуют различные модификации метода квадратичной аппроксимации, различающиеся способом выбора на каждомk-м шаге трех точек x1k, x2k, x3kдля аппроксимации целевой функции.
Метод кубической аппроксимации
В этом методе целевая функция аппроксимируется многочленом третьей степени, причем для аппроксимирующего многочлена используются значениянетолько самой целевой функции но и ее производной. Рассмотрим вариант этого метода, основанный на кубической интерполяционном многочлене Эрмита.
Лекция 3
Методы многомерной безусловной оптимизации
Ранее рассматривались одномерные задачи оптимизации, в которых целевая функция зависит лишь от одного аргумента. Однако в большинстве реальных задач оптимизации, представляющих практический интерес, целевая функция зависит от многих проектных параметров. В частности, рассмотренная выше задача об определении сопротивления дороги движению автомобиля на самом деле является многомерной, поскольку здесь наряду со скоростью имеются и другие проектные параметры(качество покрытия, уклон, температура и др.). Минимум дифференцируемой функций многих переменныхu= f(x1, x2, …, xn) можно найти, исследуя ее значения в критических точках, которые определяются из решения системы дифференциальных уравнений
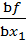 = 0,
= 0,  = 0, …,
= 0, …, 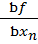 = 0.
= 0.
Пример: ранее была рассмотрена задача об определении оптимальных размеров контейнера объемом 1м3. Задача свелась к минимизации его полной поверхности, которая в данном случае является целевой функцией
S =2(x1x2 +  +
+  )
)
В соответствии с указанными дифференциальными уравнениями получим систему
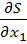 = 2(x2 -
= 2(x2 -  ) =0.
) =0.
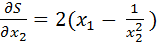 = 0.
= 0.
Отсюда находим  =
=  = 1м,
= 1м, 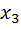 =
= 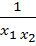 = 1м. Таким образом, оптимальной формой контейнера в данном случае является куб, длина ребра которого равна 1м. Рассмотренный метод можно использовать лишь для дифференцируемой функции. Но и в этом случае могут возникнуть серьезные трудности при решении системы нелинейных уравнений. Во многих случаях никакой формулы для целевой функции нет, а имеется лишь возможность определения ее значений в произвольных точках рассматриваемой области с помощью некоторого вычислительного алгоритма или физических измерений. Задача состоит в приближенном определении наименьшего значения функции во всей области при известных ее значениях в отдельных точках. Для решения подобной задачи в области проектирования G, в которой ищется минимум целевой функции U= f(x1, x2 …,xn) можно провести дискретное множество точек (узлов) путем разбиения интервалов изменения параметров x1, x2, …, xnна части с шагом h1, h2, …hn. В полученных узлах можно вычислить значения целевой функции и среди этих значений найти наименьшее. Следует отметить, что такой метод может быть использован для функции одной переменной. В многомерных задачах оптимизации, где проектных параметров можетбыть несколько, этот метод потребовал бы слишком большого объема вычислений. Существуют специальные численные методы, основанные на целенаправленном поиске.
= 1м. Таким образом, оптимальной формой контейнера в данном случае является куб, длина ребра которого равна 1м. Рассмотренный метод можно использовать лишь для дифференцируемой функции. Но и в этом случае могут возникнуть серьезные трудности при решении системы нелинейных уравнений. Во многих случаях никакой формулы для целевой функции нет, а имеется лишь возможность определения ее значений в произвольных точках рассматриваемой области с помощью некоторого вычислительного алгоритма или физических измерений. Задача состоит в приближенном определении наименьшего значения функции во всей области при известных ее значениях в отдельных точках. Для решения подобной задачи в области проектирования G, в которой ищется минимум целевой функции U= f(x1, x2 …,xn) можно провести дискретное множество точек (узлов) путем разбиения интервалов изменения параметров x1, x2, …, xnна части с шагом h1, h2, …hn. В полученных узлах можно вычислить значения целевой функции и среди этих значений найти наименьшее. Следует отметить, что такой метод может быть использован для функции одной переменной. В многомерных задачах оптимизации, где проектных параметров можетбыть несколько, этот метод потребовал бы слишком большого объема вычислений. Существуют специальные численные методы, основанные на целенаправленном поиске.
Метод покоординатного спуска
Пусть требуется найти наименьшее значение целевой функции U=f(x1, x2 … xn). В качестве начального приближения выберем в n – мерном пространстве некоторую точку М0с координатами 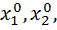 …,
…,  . Зафиксируем все координаты функции u, кроме первой. Тогда u= f(x1,
. Зафиксируем все координаты функции u, кроме первой. Тогда u= f(x1,  , …,
, …,  ) – функция одной переменной x1.
) – функция одной переменной x1.
Решая одномерную задачу оптимизации для этой функции, мы от точки M0 переходим к точке M1 (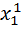 ,
,  , …,
, …,  ), в которой функция u принимает наименьшее значение по координате x1 при фиксированных остальных координатах. В этом состоит первый шаг процесса оптимизации, состоящей в спуске по координате x1. Теперь зафиксируем все координаты, кроме x2, и рассмотрим функцию этой переменной u=f(
), в которой функция u принимает наименьшее значение по координате x1 при фиксированных остальных координатах. В этом состоит первый шаг процесса оптимизации, состоящей в спуске по координате x1. Теперь зафиксируем все координаты, кроме x2, и рассмотрим функцию этой переменной u=f(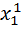 ,
,  ,
,  ,…,
,…,  ). Снова решая одномерную задачу оптимизации, находим ее наименьшее значение приx2 =
). Снова решая одномерную задачу оптимизации, находим ее наименьшее значение приx2 = 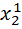 , т.е. в точке M2 (
, т.е. в точке M2 (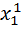 ,
, 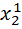 ,
,  , …,xn). Аналогично проводится спуск по координатам x3, x4, … xn, а затем процедура снова повторяетсяот x1 до xn.В результате этого процесса получается последовательность точек M0, M1, …, в которых значения целевой функции составляют монотонно убывающую последовательность f(M0)
, …,xn). Аналогично проводится спуск по координатам x3, x4, … xn, а затем процедура снова повторяетсяот x1 до xn.В результате этого процесса получается последовательность точек M0, M1, …, в которых значения целевой функции составляют монотонно убывающую последовательность f(M0) 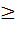 f(M1)
f(M1) 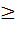 …. На любом k-м шаге этот процесс можно прервать, и значение f(Mk) принимается в качестве наименьшего значения целевой функции в рассматриваемой области. Таким образом, метод покоординатного спуска сводит задачу о нахождении наименьшего значения функции многих переменных к многократному решению одномерных задач оптимизации по каждому проектному параметру.
…. На любом k-м шаге этот процесс можно прервать, и значение f(Mk) принимается в качестве наименьшего значения целевой функции в рассматриваемой области. Таким образом, метод покоординатного спуска сводит задачу о нахождении наименьшего значения функции многих переменных к многократному решению одномерных задач оптимизации по каждому проектному параметру.
Y
| M |
М0M1x
Проиллюстрируем данный метод геометрически для случая функции двух переменных z= f(x, y), описывающей некоторую поверхность в трехмерном пространстве.На рисунке нанесены линии уровня этой поверхности. Процесс оптимизации в этом случае проходит следующим образом. Точка M0(x0,y0) описывает начальное приближение. Проводя спуск по координате x попадем в точкуM1 (x1, y0) далее двигаясь параллельно оси ординат, придем в точку M2(x1, y1) и т.д. Важным здесь является вопрос о сходимости рассматриваемого процесса оптимизации. Другими словами, будет ли последовательность значений целевой функции f(M0), f(M1), cходиться к наименьшему ее значению в данной области? Это зависит от вида самой функции и вида начального приближения. Для функции двух переменных очевидно, что метод неприменим в случае наличия изломов в линиях уровня. Это соответствует так называемому оврагу на поверхности. Здесь возможен случай, когда спуск по одной координате приводит на «дно» оврага. Тогда движение вдоль другой координаты ведет к возрастанию функции, соответствующему подъему на «берег» оврага. Поскольку поверхности типа «оврага» встречаются в инженерной практике, то при использовании метода покоординатного спуска следует убедиться что решаемая задача не имеет этого недостатка. Для гладких функций при удачно выбранном начальном приближении (в некоторой окрестности минимума) процесс сходится к минимуму. К достоинствам метода покоординатного спуска следует также отнести возможность использования простых алгоритмов одномерной оптимизации.
Метод градиентного спуска
Направление наискорейшего спуска соответствует направлению наибольшего убывания функции. Из математики известно, что направление наискорейшего возрастания функции двух переменных u=f(x,y) характеризуется ее градиентом
где e1, e2 – единичные векторы (орты) в направлении координатных осей. Следовательно, направление противоположное градиентному, укажет путь, ведущий вниз вдоль наиболее крутой линии. Методы основанные на выборе пути с помощью градиента, называются градиентными. Идея метода градиентного спуска: выбираем некоторую начальную точку и вычисляем в ней градиент рассматриваемой функции. Делаем шаг в направлении, обратному градиенту. В результате приходим в точку, значение функции в которой обычно меньше первоначального. Если это условие не выполнено, т.е. значение функции не изменилось либо даже возросло, то нужно уменьшить шаг. В новой точке процедуру повторяем: вычисляем градиент и снова делаем шаг в обратном направлении. Процесс продолжается до получения наименьшего значения целевой функции. Момент окончания поиска наступит тогда, когда движение из полученной точки с любым шагом приводит к возрастанию значения целевой функции. Строго говоря, если минимум функции достигается внутри рассматриваемой области, то в этой точке градиент равен нулю, что также может служить сигналом об окончании процесса оптимизации.
Симплекс – метод
Симплексный метод является универсальным методом, которым можно решить любую задачу линейного программирования. Идея симплексного метода состоит в следующем. Используя систему ограничений, приведенную к общему виду, т.е. к системе mлинейных уравнений с nпеременными (m  ), находят ее любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока ненаходится решение, которое является оптимальным.Если первоенайденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляют переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком-то шаге не получится допустимое базисное решение. После этого к нему применяют механизм изложенного симплексного метода. Таким образом, применение симплексного метода распадается на два этапа: 1. нахождение допустимого базисного решения системы ограничений 2 нахождение оптимального решения. При этом каждый этап может включить несколько шагов соответствующих тому или иному базисному решению. Рассмотрим практическую задачу об использовании сырья.
), находят ее любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока ненаходится решение, которое является оптимальным.Если первоенайденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляют переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком-то шаге не получится допустимое базисное решение. После этого к нему применяют механизм изложенного симплексного метода. Таким образом, применение симплексного метода распадается на два этапа: 1. нахождение допустимого базисного решения системы ограничений 2 нахождение оптимального решения. При этом каждый этап может включить несколько шагов соответствующих тому или иному базисному решению. Рассмотрим практическую задачу об использовании сырья.
Для изготовления шкафов и буфетов деревообделочный завод применяет древесину четырех видов. Запасы древесины по каждому виду ограничены и составляют соответственно 120, 160, 120, 80 ед. Количество единиц древесины каждого вида, необходимое для изготовления одного шкафа и одного буфета, а так же прибыль получаемая заводом от реализации единицы продукции представлены в таблице
Виды древесины Запасы древесины Количество единиц древесины
Шкафы буфеты
1 120 0 4
2 160 4 0
3 120 2 2
4 80 1 2
Прибыль 2 3
Требуется составить такой план выпуска продукции, который бы обеспечил предприятию наибольшую прибыль от реализации всей продукции.
Математическая формулировка задачи: пусть x1 и x2 –соответственно количество шкафов и буфетов, запланированных к производству. Так как количество древесины по каждому виду ограничено, то должны выполняться неравенства
0*x1 +4x2  120
120
4x1 +0*x2  160
160
2x1 +2x2  120
120
X1 +2x2  80
80
Эта система неравенств и является системой ограничений данной задачи. Целевая функция (линейная форма), выражающая прибыль предприятия, имеет вид F= 2x1 +3x2. Итак, задача сводится к нахождению максимума функции F = 2x1+ 3x2 при ограничениях
4x2  120
120
4x1  160
160
2x1 + 2x2  120
120
x1 + 2x2  80
80
x1  , x2
, x2 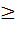 0
0
Для сведения системы ограничений – неравенств к системе уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные x3, x4, x5,x6.В условиях данной задачи они имеют конкретное экономическое содержание, а именно выражают объем остатков древесины каждого вида после выполнения плана по выпуску продукции. После введения добавочных переменных получим систему уравнений 4x2 + x3 = 120
4x1 +x4 = 160
2x1 + 2x2 + x5 = 120
x1 + 2x2 + x6 = 80
xj  (j= 1, 2, …, 6).
(j= 1, 2, …, 6).
Нужно найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало линейную форму F =2x1+ 3x2.
Так как система ограничений есть система четырех независимых уравнений с шестью переменными, то число основных переменных должно равняться четырем, а число неосновных – двум. Для решения задачи симплексным методом прежде всего нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаточно взять в качестве основных добавочные переменные x3, x4, x5,x6.Так как коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель. Считая неосновные переменные x1 и x2равными нулю, получим базисное решение (0; 0;120;160;120;80), которое к тому же оказалось допустимым. Поэтому здесь отпадает надобность в применении первого этапа симплексного метода. Переходим сразу ко второму этапу, т.е. к поискам оптимального решения. 1 шаг. Основные переменные:x3, x4, x5,x6: неосновные переменные: x1, x2. В системе основные переменные выразим через неосновные. Для того, чтобы судить, оставить ли неосновные переменные в числе неосновных или их выгоднее с точки зрения приближения к оптимальному решению перевести в основные, следует выразить через них и линейную форму (в данном случае она выражена через переменные x1иx2). Тогда получим
x3= 120 - 4x2
x4 = 160 – 4x1
x5= 120 – 2x1 -2x2
x6= 80 –x1 - 2x2
F = 2x1 + 3x2
При x1 = x2 = 0 имеем x3 =120, x4 = 160, x5 = 120, x6 =80.Что дает базисное решение (0; 0; 120; 160; 120; 80), которое мы приняли за исходное. При этом базисном решении значение линейной формы F = 2x1 +3x2 = 0. Когда полагали x1 = x2= 0 (завод ничего не выпускает), была поставлена цель – найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого первоначального решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных x1x2. Иными словами, эти переменные невыгодно считать неосновными, т.е. равными нулю их нужно перевести в число основных. Это и означает переход к новому базисному решению. При симплексном методе на каждом шаге решения предполагается перевод в число основных только одной из свободных переменных. Переведем в число основных переменную x2, так как она входит в выражение линейной формы с бȯльшим коэффициентом.Как только одна из свободных переменных переходит в число основных, одна из основных должна быть переведена на ее место в число неосновных. Какую же из четырех основных переменных нужно вывести? Ответить на этот вопрос помогут следующие рассуждения. Значение x2 следует сделать как можно большим, так как это соответствует конечной цели – максимизации F. Однако оказывается, что увеличение x2 может продолжаться только до известных границ, а именно до тех пор, пока не нарушится требование неотрицательности переменных.Так из первого уравнения системы следует, что переменная x2 не должна превышать числа 120/4, т.е. x2  30, поскольку только при этих значениях x2 переменная x3 остается положительной. (если x2 = 30, то x3 =0; если же x2
30, поскольку только при этих значениях x2 переменная x3 остается положительной. (если x2 = 30, то x3 =0; если же x2 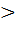 30, то x3
30, то x3  0). Из третьего уравнения системы следует, что x2
0). Из третьего уравнения системы следует, что x2  120/2, т.е. x2
120/2, т.е. x2  60 из четвертого –что x2
60 из четвертого –что x2  80/2 т.е. x2
80/2 т.е. x2  40. (во второе уравнение переменная x2 не входит). Всем этим условиям удовлетворяет x2
40. (во второе уравнение переменная x2 не входит). Всем этим условиям удовлетворяет x2  30.Иными словами, для ответа на вопрос, какую переменную нужно перевести в число неосновных, нужно принять x2 = min
30.Иными словами, для ответа на вопрос, какую переменную нужно перевести в число неосновных, нужно принять x2 = min  = min
= min  = 30. Тогда x3 переходит в число неосновных переменных, а x4 и x5 останутся положительными. 2 шаг. Основные переменные: x2, x4, x5, x6; неосновные переменные x1, x3.Выразим основные переменные через неосновные. В системе берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при x2. В данном случае это первое уравнение, которое выделено чертой. Выразим из этого уравнения x2,имеем x2 = 30- 0,25x3. Подставим это выражение x2во все остальные уравнения системы и в линейную форму Fи приведя подобные члены, получим
= 30. Тогда x3 переходит в число неосновных переменных, а x4 и x5 останутся положительными. 2 шаг. Основные переменные: x2, x4, x5, x6; неосновные переменные x1, x3.Выразим основные переменные через неосновные. В системе берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при x2. В данном случае это первое уравнение, которое выделено чертой. Выразим из этого уравнения x2,имеем x2 = 30- 0,25x3. Подставим это выражение x2во все остальные уравнения системы и в линейную форму Fи приведя подобные члены, получим
X2= 30 – 0.25x3
X4= 160 – 4x1
X5= 60 – 2x1 + 0.5x3
X6 = 20 – x1 + 0.5x3.
F = 90 +2x1 – 0. 75x3.
При x1 = x3 = 0. Имеем F = 90. Это уже лучше, чем на первом шаге, но не искомый максимум. Дальнейшее увеличение функции возможно за счет введения переменной x1 в число основных, так как эта переменная входит в выражение Fс положительным коэффициентом, поэтому ее увеличение приводит к увеличению линейной формы и ее невыгодно считать неосновной, т.е. равной нулю. Для ответа на вопрос, какую переменную вывести из основных в неосновные, примем x1 =min  = 20. Тогда x6 = 0 и x6переходит в число неосновных переменных, а x4и x5остаются при этом положительными. Первое уравнение не используется при нахождении указанного минимума, т.к. x1не входит в это уравнение. 3 шаг.Основные пременные: x1, x2,x4, x5;неосновные переменные x3, x6. Выразим основные переменные и линейную форму через неосновные. Из последнего уравнения системы (оно выделено) имеем x1 = 20 +0.5x3–x6. Подставляя это выражениев остальные уравнения и в линейную форму, получим
= 20. Тогда x6 = 0 и x6переходит в число неосновных переменных, а x4и x5остаются при этом положительными. Первое уравнение не используется при нахождении указанного минимума, т.к. x1не входит в это уравнение. 3 шаг.Основные пременные: x1, x2,x4, x5;неосновные переменные x3, x6. Выразим основные переменные и линейную форму через неосновные. Из последнего уравнения системы (оно выделено) имеем x1 = 20 +0.5x3–x6. Подставляя это выражениев остальные уравнения и в линейную форму, получим
x1= 20 +0.5x3 – x6
x2 = 30 – 0.25x3
x4 = 80 – 2x3 +4x6
x5 = 20 – 0.5x3 + 2x6
F = 130 +0.25x3 – 2x6.
Из выражения линейной формы следует, что ее максимальное значение еще не получено, так как возможно увеличение Fза счет введения в основные переменные x3(она имеет положительный коэффициент). Полагаем x3 = min 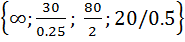 = 40. Здесь мы впервые встречаемся с двумя положениями, которые требуют дополнительных разъяснений. Во- первых, хотя переменнаяx3и входит в выражение для x1 (первое уравнение сис
= 40. Здесь мы впервые встречаемся с двумя положениями, которые требуют дополнительных разъяснений. Во- первых, хотя переменнаяx3и входит в выражение для x1 (первое уравнение сис
 2017-10-25
2017-10-25 1967
1967