2017-10-25
1479
Рассмотрим произвольный обратимый процесс в идеальном газе. Подставив значение dq из выражения для первого закона термодинамики 
в (3.12) и учитывая, что для идеального газа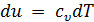 
, получим:
Так как для идеального газа 
, то 
.
Интегрируя это уравнение от состояния газ в точке 1 до его состояния в точке 2 (рис. 3.9), получим
. (3.12)
Из уравнений состояний в этих точках 
и 
следует, что 
.
Тогда уравнение (3.12) можно преобразовать к следующему виду
.
Следовательно, 
. (3.13)
Таким образом, изменение энтропии газа в обратимом процессе можно определить, зная параметры его состояния в начале и конце этого процесса.
Все эти уравнения получены с использованием уравнения 
, поэтому справедливы только для обратимых процессов. Но, так как энтропия является функцией состояния, эти формулы дают значения изменения энтропии идеального газа независимо от того, в каком обратимом процессе достигнуто это состояние.
3.8. Т, s - координаты
В теории тепловых двигателей наряду с p, υ- координатами часто используется изображение графиков равновесных процессов в T, s - координатах. На рис. 3.11 в таких координатах изображен некий процесс 1 - 2. Если этот процесс обратим, то, поскольку для обратимого процесса 
или 
, площадь заштрихованной области, соответствующая элементарному изменению энтропии на 
при некоторой температуре Т, эквивалентна элементарному количеству теплоты , подведенному к рабочему телу в этом элементарном процессе.
 |  |
| Рис. 3.11 | Рис. 3.12 |
Вся теплота, подведенная к рабочему телу в обратимом процессе 1-2 (в расчете на единицу массы), определится по формуле
и изобразится в Т, s-координатах площадью фигуры а12b, ограниченной линией 1-2, осью абсцисс и вертикальными отрезками 1-а и 2 - b.
Рассмотрим далее в Т, s -координатах прямой цикл 1а2b1 (рис. 3.12). В процессе 1-а-2 теплота q 1 подводится к рабочему телу в количестве, эквивалентном площади фигуры 1'1а22'1¢. В процессе 2b1 от рабочего тела отводится теплота q 2 в количестве, эквивалентном площади фигуры 2'2b11'2'. Очевидно, что площадь, ограниченная циклом 1а2b1, равна
,
т. е. работе цикла (если он обратим).
