Понятие описательной статистики и ее показателей для выборок

Начальный раздел математической статистики – описательная статистика занимается характеристикой (описанием) случайного рассеяния по выборочной совокупности данных, оценивает закон распределения и обобщенные выборочные характеристики (параметры). Их смысл пояснялся при имитации совокупности случайных данных кучей песка, и ниже рассматривается более строго.

Параметры положения

Они понимаются, как оценки положения центра распределения (его расположения на числовой оси случайной величины). Центр распределения характеризуется средним случайной величины; серединой упорядоченной совокупности и наиболее часто встречающейся величиной. Эти параметры положения имеют размерность самих случайных величин.

1. Выборочное среднее арифметическое является наиболее известным и употребительным параметром положения случайной величины х_i:

,

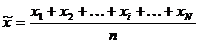где n – объем выборки. Если варианты сгруппированы в n интервалов со средними значениями х₁, х₂, …, х_i, …, х_n, и числом вариант в каждом n₁, n₂, …, n_i, …, n_n, то среднее арифметическое рассчитывается как среднее взвешенное:

,

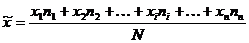где N= n₁+n₂+…+n_i+…+n_n.

Среднее взвешенное всей генеральной совокупности, подсчитываемое с использованием вероятностей случайной величины в качестве весов, называется математическим ожиданием. Очевидно, среднее взвешенное в выборке является оценкой среднего взвешенного генеральной совокупности и оценкой математического ожидания генеральной совокупности.

Среднее взвешенное является начальным моментом первого порядка, который имеет обозначение m. Для непрерывных случайных величин он, математическое ожидание (и среднее взвешенное) определяются интегралами:

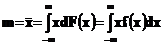
Для дискретных случайных величин, вместо интегралов берутся соответствующие суммы. Можно показать, что выборочное среднее (оценка математического ожидания) имеет минимальную сумму квадратов отклонений от значений случайной величины в выборке. Среднему случайной величины при имитации распределениярассеяниемпескаотвечает центр тяжести кучи. Центр тяжести одномерной массы, распределенной с некоторой плотностью вдоль оси значений случайной величины, является начальным моментом первого порядка, т.е. средним взвешенным.

При симметричном распределении случайной величинысреднее арифметическое (математическое ожидание), как и центр тяжести одномерной массы, симметрично распределенной вдоль оси, совпадают с центром симметрии.

Из закона больших чисел следует, что с увеличением объема выборки ее среднее арифметическое стремится к среднему арифметическому генеральной совокупности (математическому ожиданию).

2. Медиана случайной величины – это такое ее значение, которое делит совокупность на две равные части: большие и меньшие медианы.

В куче песка,имитирующей совокупность случайных величин, медиана ­– линия в основании, вертикальная плоскость через которую делит кучу на две части с равным числом песчинок.

Площадь под графиком плотности вероятностей одномерного распределения случайной величины делится пополам по медианному значению. В симметричном распределении медиана и математическое ожидание совпадают.

3. Мода распределения случайной величины – такое ее значение, которое встречается наиболее часто. Мода распределения отвечает горизонтальной проекции вершины кучи песка,имитирующей совокупность случайных величин. Мода соответствует максимуму плотности вероятностей. В симметричном распределении мода, медиана и математическое ожидание совпадают.

Параметры рассеяния

К параметрам рассеяния относятся оценки степени разброса случайной величины. Эти параметры в аналогии рассеяния случайной величины с кучей песка характеризуют ее компактность, близость песчинок к центру.

1. Дисперсия выборки определяется как математическое ожидание квадрата отклонения случайной величины от своего математического ожидания, т.е. средний квадрат отклонений случайной величины от ее среднего.

Дисперсия, которую принято обозначать D является центральным моментом второго порядка, обозначаемым m₂. Т.е. D=m₂.

Дисперсия непрерывной случайной величины определяется интегралом: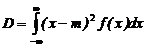

Для выборки случайных величин объемом N вариант оценка дисперсии подсчитывается по формуле

,

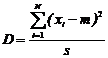где s – число степеней свободы. Величина s определяется количеством вариант за вычетом числа наложенных связей, т.е.s показывает, сколько вариант в выборке может изменяться случайным образом при наложенном условии. Так сумма двух случайных чисел имеет 2 степени свободы, поскольку каждое из них может выбираться случайно. Но если наложить условие равенства среднего из чисел некоторому значению, то только одно число выбирается случайно, а второе определяется условием из соответствующего ему уравнения. Поэтому число степеней свободы определится как 2-1=1.

При определении дисперсии с априорно известным математическим ожиданием s=N. Но, если в качестве оценки математического ожидания берется его выборочная величина по данным той же выборки, то тем самым на нее накладывается одно условие – варианты должны удовлетворять уравнению:

.

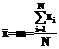Соответственно число степеней свободы составит s=N-1. Когда N достаточно велико, N»N-1, т.е. уменьшением числа степеней свободы можно пренебречь. Но в общем случае оценка дисперсии, без учета числа степеней свободы оказывается заниженной и называется смещенной. Оценка дисперсии, подсчитанная с учетом числа степеней свободы, является несмещенной.

2. Стандартное отклонение (стандарт) – это среднеквадратичное отклонение вариант в обе стороны (со знаками ±) от среднего арифметического. Стандартное отклонение (d) является квадратным корнем из дисперсии – удовлетворяет уравнению D=d². Оценка стандарта, как и дисперсии, без учета числа степеней свободы занижена, является смещенной, при учете числа степеней свободы – несмещенной. В аналогии случайного рассеяния и кучи песка стандарту отвечает ширина кучи на высоте примерно 1/3 от вершины.

3. Коэффициент вариации – это относительный показатель рассеяния, равный отношению стандартного отклонения к среднему значению случайной величины. Если обозначить коэффициент вариации V, то V=d/m= d/ .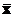

4. Размах случайной величины – это разность между максимальным и минимальным значениями, приблизительно в 6 раз превышающая стандарт. В аналогии рассеяния случайной величины с кучей песка размаху отвечает ширина кучи в основании, т.е. границы области рассеяния.

Параметры формы распределения

Основными параметрами формы распределения случайной величины являются показатели асимметрии и островершинности.

1. Асимметрия (скошенность) обозначается А и характеризуется относительной величиной центрального момента третьего порядка: А= m₃/d³.

В симметричных распределениях m₃=0 и А=0, т.е. асимметрия, естественно, отсутствует. При положительной асимметрии кривая плотности вероятностей затянута вправо (в сторону больших значений случайной величины), при отрицательной асимметрии – влево.

Нормальное распределение случайной величины является симметричным, А=0. Статистически значимое отклонение асимметрии от нуля указывает на несогласие тестируемого распределения с симметричным законом и, в частности, с нормальным.

2.Эксцесс (крутость) обозначается Е и выражается через относительную величину центрального момента четвертого порядка формулой Е= m₄/d⁴-3. У нормального распределения эксцесс равен 0, отклонение от которого указывает на несогласие с нормальным законом.