В механике под твердым телом понимают систему материальных точек, расстояние между любыми двумя точками которого в процессе движения остается неизменным. Поэтому все результаты, полученные в предыдущих темах (“Динамика материальной точки”, “Закон сохранения импульса”, “Закон сохранения энергии” и “Закон сохранения момента импульса”) для системы материальных точек, применимы и к твердому телу.
Момент инерции твердого тела
Момент инерции – это величина, зависящая от распределения масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. При вращении твердого тела вокруг неподвижной оси момент инерции тела относительно этой оси определяется выражением
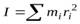 ,
,
где 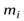 - элементарные массы тела;
- элементарные массы тела; 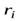 - их расстояния от оси вращения.
- их расстояния от оси вращения.
Момент инерции тела относительно какой-либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла
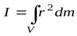 , (1)
, (1)
где 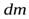 – масса элемента тела, находящегося на расстоянии
– масса элемента тела, находящегося на расстоянии 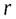 от интересующей нас оси. Интегрирование должно производиться по всему объему тела.
от интересующей нас оси. Интегрирование должно производиться по всему объему тела.
Аналитическое вычисление таких интегралов возможно только в простейших случаях тел правильной геометрической формы.
Если известен момент инерции тела относительно какой-либо оси, можно найти момент инерции относительно любой другой оси, параллельной данной. Используя теорему Штейнера, согласно которой момент инерции тела 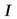 относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс тела
относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс тела 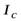 и параллельной данной оси, и произведения массы тела т на квадрат расстояния между осями
и параллельной данной оси, и произведения массы тела т на квадрат расстояния между осями 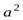 :
:
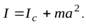 (2)
(2)
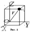 Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений.
Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений.
Рассмотрим некоторую точку твердого тела массой 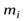 и с координатами
и с координатами 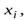
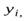
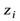 относительно прямоугольной системы координат (рис. 1). Квадраты расстояний ее до координатных осей
относительно прямоугольной системы координат (рис. 1). Квадраты расстояний ее до координатных осей 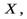
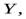
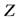 равны соответственно
равны соответственно 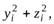
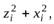
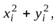 а моменты инерции относительно тех же осей
а моменты инерции относительно тех же осей
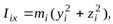
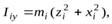
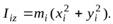 (3)
(3)
Сложив эти равенства и просуммировав по всему объему тела
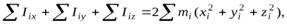 (4)
(4)
получим
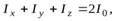 (5)
(5)
где 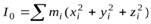 – момент инерции тела относительно точки.
– момент инерции тела относительно точки.
Из этого выражения можно получить связь между моментами инерции плоского тела, относительно осей 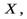
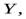
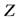 . Пусть масса плоского тела сосредоточена в плоскости
. Пусть масса плоского тела сосредоточена в плоскости 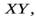 т.е. координата
т.е. координата 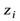 любой точки такого тел равна нулю, тогда из
любой точки такого тел равна нулю, тогда из
уравнений (3) и (4) следует, что
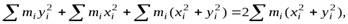
или
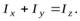 (6)
(6)
Вращение твердого тела вокруг неподвижной оси
Рассмотрим твердое тело массой 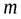 , вращающееся вокруг неподвижной оси с угловой скоростью
, вращающееся вокруг неподвижной оси с угловой скоростью 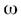 . Для того чтобы получить уравнение, описывающее это движение, применим уравнение моментов относительно оси, полученное в разделе “ Закон сохранения момента импульса”
. Для того чтобы получить уравнение, описывающее это движение, применим уравнение моментов относительно оси, полученное в разделе “ Закон сохранения момента импульса”
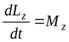 , (7)
, (7)
напомним, что в этом уравнении 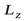 и
и 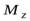 – момент импульса и момент силы относительно оси, вокруг которой вращается твердое тело.
– момент импульса и момент силы относительно оси, вокруг которой вращается твердое тело.
Момент импульса некоторой точки тела массой 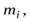 вращающейся по окружности радиуса
вращающейся по окружности радиуса 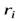 со скоростью
со скоростью 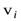 , равен
, равен
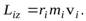
Просуммировав по всему объему тела, учитывая, что 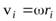 получим
получим
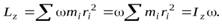
Таким образом, момент импульса твердого тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции тела относительно этой оси на его угловую скорость.
Подставляя полученное выражение в (7), получим уравнение динамики твердого тела, вращающегося вокруг неподвижной оси,
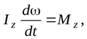 или
или 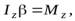 (8)
(8)
где 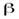 – угловое ускорение тела.
– угловое ускорение тела.
Найдем кинетическую энергию вращающегося тела. Для этого просуммируем по всему объему тела кинетические энергии отдельных его частей
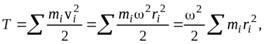
или
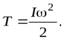 (9)
(9)
Зная зависимость момента сил, действующих на тело, от угла поворота, можно найти работу этих сил при повороте тела на конечный угол 
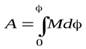 .
.
Плоское движение твердого тела
Напомним, что плоское движение твердого тела можно интерпретировать как суперпозицию поступательного и вращательного движения. В разделе “Динамика материальной точки” было получено, что поступательное движение системы материальных точек можно представить как движение материальной точки, масса которой равна массе всей системы, движущейся со скоростью, равной скорости центра масс 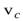 системы, т.е.
системы, т.е.
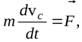 (10)
(10)
где 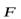 – сумма внешних сил, действующих на систему. Это уравнение применимо и к поступательному движению твердого тела.
– сумма внешних сил, действующих на систему. Это уравнение применимо и к поступательному движению твердого тела.
В разделе “Закон сохранения момента импульса” было показано, что в подвижной системе отсчета, связанной с центром масс, уравнение моментов имеет такой же вид, как и в неподвижной системе, т.е. для вращательного движения тела относительно оси, проходящей через центр масс, можно записать (см. уравнение 8)
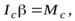 (11)
(11)
где 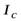 и
и 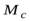 – момент инерции и момент сил относительно оси, проходящей через центр масс твердого тела.
– момент инерции и момент сил относительно оси, проходящей через центр масс твердого тела.
Таким образом, уравнения (10) и (11) описывают плоское движение твердого тела.
В тех случаях, когда известно положение мгновенной оси вращения тела, и если мгновенная ось движется параллельно центру масс тела, можно применить уравнение моментов относительно мгновенной оси вращения
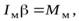 (12)
(12)
где 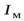 и
и 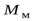 – момент инерции и момент сил относительно мгновенной оси. В этом случае для решения задачи достаточно только одного уравнения (12)
– момент инерции и момент сил относительно мгновенной оси. В этом случае для решения задачи достаточно только одного уравнения (12)
Получить выражения для кинетической энергии твердого тела при плоском движении, можно воспользовавшись теоремой Кенига, сформулированной для системы материальных точек, применив ее к твердому телу. Согласно этой теореме кинетическая энергия системы частиц складывается из кинетической энергии в системе отсчета, связанной с центром масс (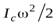 ) и кинетической энергии, связанной с движением системы частиц как целого (
) и кинетической энергии, связанной с движением системы частиц как целого (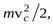 где
где 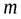 – масса тела), т.е.
– масса тела), т.е.
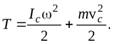 (13)
(13)
Вопросы для самоконтроля
1.Мерой инертности тела является
а) только масса;
б) только момент инерции тела относительно точки;
в) только момент инерции тела относительно оси;
г) и масса и момент инерции относительно оси.
Укажите ошибочные утверждения.
2. Теорема Штейнера утверждает, что
а) момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями;
б) момент инерции тела относительно оси, проходящей через центр масс, равен сумме момента инерции тела относительно произвольной оси и произведения массы тела на квадрат расстояния между осями;
в) момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
Укажите правильную формулировку теоремы.
3. Маленький шарик массой 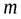 движется по окружности радиуса
движется по окружности радиуса 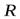 . Момент инерции шарика относительно оси, перпендикулярной плоскости движения и проходящий через центр окружности равен:
. Момент инерции шарика относительно оси, перпендикулярной плоскости движения и проходящий через центр окружности равен:
а) 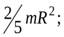 б)
б) 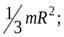 в)
в) 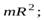 г)
г) 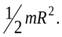
Укажите правильное утверждение.
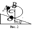 4. Шар скатывается без проскальзывания с наклонной плоскости. При описании движения шара необходимо записать уравнение моментов относительно оси, перпендикулярной плоскости рисунка 2 и проходящей через некоторую точку шара. Через какие точки
4. Шар скатывается без проскальзывания с наклонной плоскости. При описании движения шара необходимо записать уравнение моментов относительно оси, перпендикулярной плоскости рисунка 2 и проходящей через некоторую точку шара. Через какие точки
а) 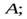 б)
б) 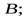 в)
в) 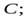 г)
г) 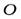
должна проходить ось, чтобы уравнение моментов имело вид 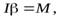 где
где 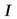 и
и 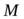 – момент инерции и момент сил относительно этой оси,
– момент инерции и момент сил относительно этой оси, 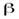 – угловое ускорение шара.
– угловое ускорение шара.
Укажите правильные утверждения.
5. Под действием некоторой постоянной силы 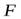 твердое тело массой
твердое тело массой 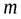 начинает двигаться, совершая плоское движение. Через некоторое время угловая скорость тела равна
начинает двигаться, совершая плоское движение. Через некоторое время угловая скорость тела равна 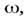 а скорость центра масс равна
а скорость центра масс равна 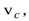 при этом точка приложения силы совершила перемещение
при этом точка приложения силы совершила перемещение 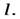 Какие из уравнений позволяют найти работу этой силы:
Какие из уравнений позволяют найти работу этой силы:
а) 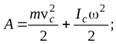 б)
б) 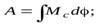 в)
в) 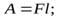
г) 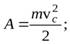 д)
д) 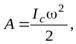
где 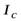 и
и 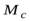 – момент инерции и момент силы относительно оси, проходящей через центр масс тела,
– момент инерции и момент силы относительно оси, проходящей через центр масс тела, 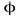 – угол поворота тела?
– угол поворота тела?
Примеры решения задач
Пример 1. Найти момент инерции тонкого однородного диска массой 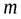 и радиуса
и радиуса 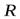 относительно: а) оси симметрии, перпендикулярной к плоскости диска; б) оси, совпадающей с диаметром диска.
относительно: а) оси симметрии, перпендикулярной к плоскости диска; б) оси, совпадающей с диаметром диска.
Р е ш е н и е. а)Выберем на диске цилиндрический слой радиуса 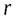 и шириной
и шириной 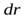 (см. рис. 3а). Так как все элементы цилиндрического слоя находятся на одном расстоянии от центра кольца, его момент инерции равен
(см. рис. 3а). Так как все элементы цилиндрического слоя находятся на одном расстоянии от центра кольца, его момент инерции равен
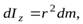 (14)
(14)
где 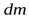 – масса кольца, которую можно найти, определив поверхностную плотность материала диска
– масса кольца, которую можно найти, определив поверхностную плотность материала диска 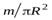 и умножив ее на площадь поверхности кольца
и умножив ее на площадь поверхности кольца 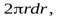 т.е.
т.е.
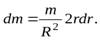
П  одставляя это значение в (14) интегрируя по
одставляя это значение в (14) интегрируя по  в пределах от 0 до
в пределах от 0 до  , найдем момент инерции диска относительно оси симметрии
, найдем момент инерции диска относительно оси симметрии
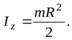 (15)
(15)
б) Для нахождения момента инерции диска относительно диаметра, например оси 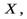 воспользуемся соотношением (6). Проведем три взаимно перпендикулярные оси
воспользуемся соотношением (6). Проведем три взаимно перпендикулярные оси 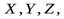 пересекающиеся в центре диска (рис. 3б). Очевидно, что
пересекающиеся в центре диска (рис. 3б). Очевидно, что 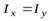 , тогда из уравнения (6) следует
, тогда из уравнения (6) следует
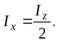
Подставляя в это выражение значение 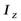 из уравнения (15), найдем момент инерции диска относительно диаметра
из уравнения (15), найдем момент инерции диска относительно диаметра
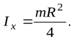
Пример 2. Найти момент инерции однородного шара массы 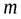 и радиуса
и радиуса 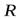 относительно оси, совпадающей с центром шара.
относительно оси, совпадающей с центром шара.
Р  е ш е н и е. Вычисление момента инерции шара прямым методом, т.е. с использованием уравнения (1) довольно трудоемкая математическая задача, поэтому для нахождения этого момента инерции воспользуемся соотношением (5). Проведем три взаимно перпендикулярные оси
е ш е н и е. Вычисление момента инерции шара прямым методом, т.е. с использованием уравнения (1) довольно трудоемкая математическая задача, поэтому для нахождения этого момента инерции воспользуемся соотношением (5). Проведем три взаимно перпендикулярные оси 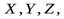 пересекающиеся в центре шара (см. рис. 4). Очевидно, что
пересекающиеся в центре шара (см. рис. 4). Очевидно, что
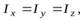
поэтому соотношение (5) перепишем в виде
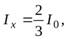 (16)
(16)
где 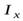 – искомый момент инерции,
– искомый момент инерции, 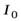 – момент инерции шара относительно центра шара.
– момент инерции шара относительно центра шара.
Для нахождения момента инерции 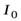 выберем тонкий сферический слой радиуса
выберем тонкий сферический слой радиуса 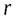 и толщиной
и толщиной 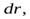 центр которого совпадает с центром шара (на рис. 4 он выделен цветом). Все элементы этого слоя находятся на одинаковом расстоянии от центра шара, поэтому его момент инерции относительно центра шара равен
центр которого совпадает с центром шара (на рис. 4 он выделен цветом). Все элементы этого слоя находятся на одинаковом расстоянии от центра шара, поэтому его момент инерции относительно центра шара равен
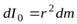 . (17)
. (17)
Объемная плотность шара равна 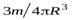 , умножая ее на объем тонкого сферического слоя
, умножая ее на объем тонкого сферического слоя 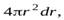 найдем массу сферического слоя
найдем массу сферического слоя
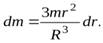
Подставляя это выражение в (17) и интегрируя в пределах от 0 до 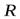 , найдем момент инерции шара относительно центра
, найдем момент инерции шара относительно центра
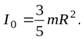
С учетом этого из уравнения (16) находим искомый момент инерции шара
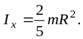
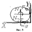 Пример 3. Однородный цилиндр радиуса
Пример 3. Однородный цилиндр радиуса 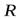 раскрутили вокруг его оси до угловой скорости
раскрутили вокруг его оси до угловой скорости 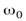 и поместили затем в угол (рис.5) Коэффициент трения между стенками угла и цилиндром равен
и поместили затем в угол (рис.5) Коэффициент трения между стенками угла и цилиндром равен 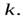 Сколько оборотов сделает цилиндр до остановки?
Сколько оборотов сделает цилиндр до остановки?
Р е ш е н и е. Расставим силы, действующие на цилиндр. Запишем уравнение, описывающее выражение цилиндра относительно его оси
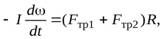 (18)
(18)
где 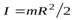 – момент инерции цилиндра относительно этой оси. Знак “–” в левой части этого уравнения обусловлен тем, что при замедленном движении модуль углового ускорения
– момент инерции цилиндра относительно этой оси. Знак “–” в левой части этого уравнения обусловлен тем, что при замедленном движении модуль углового ускорения 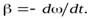 Так как нам необходимо найти число оборотов, которое сделает цилиндр до остановки, исключим из уравнения (18) время. Для этого умножим и разделим левую часть уравнения (18) на
Так как нам необходимо найти число оборотов, которое сделает цилиндр до остановки, исключим из уравнения (18) время. Для этого умножим и разделим левую часть уравнения (18) на 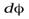
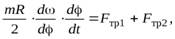
где 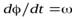 – угловая скорость вращения цилиндра в некоторый момент времени. После преобразований получим
– угловая скорость вращения цилиндра в некоторый момент времени. После преобразований получим
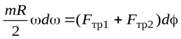 . (19)
. (19)
Прежде чем решать это уравнение, найдем выражения для сил трения. Так как центр цилиндра покоится,
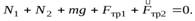
Запишем это уравнение в проекциях на оси 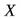 и
и 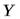 (см. рис. 5)
(см. рис. 5)
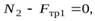
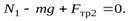
Решая эту систему уравнений, учитывая, что 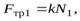 а
а 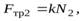 получим выражения для сил трения
получим выражения для сил трения
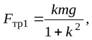
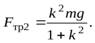
Подставляя эти выражения в уравнение (19) и интегрируя левую часть этого уравнения в пределах от 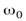 до 0, а правую часть в пределах от 0 до
до 0, а правую часть в пределах от 0 до 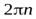 , найдем число оборотов
, найдем число оборотов 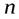 , которое сделает цилиндр до остановки
, которое сделает цилиндр до остановки
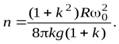
Пример 4. Однородный шар скатывается без скольжения по наклонной плоскости, составляющей угол 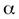 с горизонтом. Найти ускорение
с горизонтом. Найти ускорение 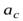 центра шара и кинетическую энергию шара через время
центра шара и кинетическую энергию шара через время 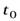 после начала движения.
после начала движения.
Р е ш е н и е. Решим задачу двумя способами.
а) Шар совершает плоское движение. Свяжем подвижную систему отсчета с центром шара. Эта система движется поступательно относительно наклонной плоскости, а шар в этой системе вращается вокруг оси, проходящей через его центр. Расставим силы, действующие на шар в процессе движения (см. рис.6). Запишем теорему о движении центра масс в проекции на ось 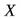 (см. рис.6)
(см. рис.6)
 (20)
(20)
У  равнение вращательного движения шара вокруг оси, проходящей через центр масс имеет вид
равнение вращательного движения шара вокруг оси, проходящей через центр масс имеет вид
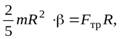 (21)
(21)
где 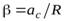 – угловое ускорение шара,
– угловое ускорение шара, 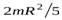 – момент инерции шара относительно оси вращения. Решая совместно уравнения (20) и (21), найдем ускорение центра шара
– момент инерции шара относительно оси вращения. Решая совместно уравнения (20) и (21), найдем ускорение центра шара 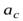 и его угловое ускорение
и его угловое ускорение 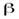
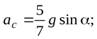
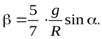 (22)
(22)
Используя формулу (13) для кинетической энергии тела, совершающего плоское движение, и учитывая, что в интересующий нас момент времени 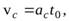 и
и 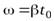 (т.к.
(т.к. 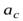 и
и 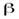 постоянные), найдем кинетическую энергию шара через время
постоянные), найдем кинетическую энергию шара через время 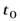 после начала движения
после начала движения
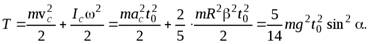
б) Так как шар катится без проскальзывания, точка соприкосновения шара 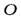 с наклонной плоскостью имеет скорость равную нулю. Поэтому прямая, перпендикулярная плоскости рисунка и проходящая через точку
с наклонной плоскостью имеет скорость равную нулю. Поэтому прямая, перпендикулярная плоскости рисунка и проходящая через точку 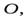 является мгновенной осью вращения. Относительно этой оси шар совершает вращательное движение, поэтому для описания движения достаточно записать уравнение (12) в виде
является мгновенной осью вращения. Относительно этой оси шар совершает вращательное движение, поэтому для описания движения достаточно записать уравнение (12) в виде
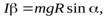 (23)
(23)
где 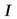 – момент инерции шара относительно мгновенной оси вращения. Согласно теореме Штейнера момент инерции
– момент инерции шара относительно мгновенной оси вращения. Согласно теореме Штейнера момент инерции 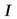 равен
равен
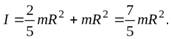
Подставляя это выражение в уравнение (23), находим ускорение центра шара 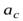 и его угловое ускорение
и его угловое ускорение 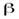 (см. уравнения (22)).
(см. уравнения (22)).
Кинетическая энергия шара, в этом случае, определяется только вращательным движением
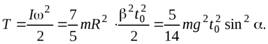
Заметим, что при любом способе решения, кинетическую энергию шара можно найти из закона сохранения энергии (сила трения работы не совершает, т.к. эта сила – сила трения покоя). Пусть за время 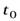 высота центра шара изменилась на
высота центра шара изменилась на 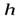 (см. рис.6), тогда
(см. рис.6), тогда
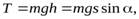 (24)
(24)
где 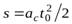 – расстояние, пройденное центром шара за время
– расстояние, пройденное центром шара за время 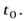 Подставляя в (24) выражение для
Подставляя в (24) выражение для 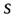 и
и 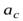 , находим кинетическую энергию шара
, находим кинетическую энергию шара
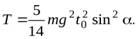
Пример 5. Однородный стержень длины 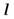 может вращаться вокруг горизонтальной оси, перпендикулярной к стержню и проходящей через один из его концов (рис. 7). Систему равномерно вращают с угловой скоростью
может вращаться вокруг горизонтальной оси, перпендикулярной к стержню и проходящей через один из его концов (рис. 7). Систему равномерно вращают с угловой скоростью 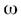 вокруг вертикальной оси. Пренебрегая трением, найти угол
вокруг вертикальной оси. Пренебрегая трением, найти угол 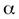 между стержнем и вертикалью.
между стержнем и вертикалью.
Р е ш е н и е. Решим задачу двумя способами. Первое решение приведем в инерциальной системе отсчета, т.е. в системе, в которой стержень вращается. Второе решение – в неинерциальной системе отсчета, жестко связанной со стержнем.
а) Система отсчета, в которой будем решать задачу, на рис. 7 не показана. Решение задачи относительно вертикальной оси вращения не даст желаемого результата, т.к. моменты сил, действующих на стержень (сила тяжести и сила реакции в точке 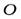 ), относительно этой оси равны нулю, и величина момента импульса остается постоянной.
), относительно этой оси равны нулю, и величина момента импульса остается постоянной.
Поэтому будем решать задачу относительно точки 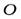 подвеса стержня. Напомним, что уравнение моментов относительно точки имеет вид
подвеса стержня. Напомним, что уравнение моментов относительно точки имеет вид
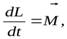
откуда видно, что направление изменения момента импульса 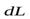 совпадает по направлению с направлением момента сил
совпадает по направлению с направлением момента сил 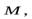 действующих на стержень, поэтому в дальнейшем это уравнение будем записывать для модулей
действующих на стержень, поэтому в дальнейшем это уравнение будем записывать для модулей 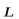 и
и 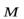
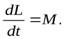 (25)
(25)
Момент силы реакции в точке 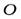 равен нулю, т.к. плечо этой силы равно нулю. Направление момента силы тяжести показано на рис.7, а величина равна
равен нулю, т.к. плечо этой силы равно нулю. Направление момента силы тяжести показано на рис.7, а величина равна
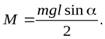 (26)
(26)
Найдем величину и направление момента импульса 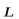 стержня относительно точки
стержня относительно точки  Для этого выделим на стержне небольшой участок длиной
Для этого выделим на стержне небольшой участок длиной 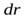 и массой
и массой 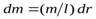 положение которого относительно точки
положение которого относительно точки 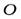 зададим радиус-вектором
зададим радиус-вектором 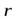 (см. рис. 7). Обозначим величину момента импульса этого участка как
(см. рис. 7). Обозначим величину момента импульса этого участка как 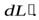 Так как стержень вращается вокруг вертикальной оси, так как показано на рисунке, скорость
Так как стержень вращается вокруг вертикальной оси, так как показано на рисунке, скорость 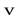 этого участка будет направлена за плоскость рисунка, поэтому как следует из определения момента импульса
этого участка будет направлена за плоскость рисунка, поэтому как следует из определения момента импульса
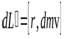 ,
,
он будет направлен перпендикулярно стержню, как показано на рис. 7. Очевидно, что направления всех моментов импульса остальных участков стержня будут иметь такое же направление, поэтому результирующий момент импульса будет также перпендикулярен стержню. Учитывая, что векторы 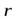 и
и 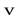 взаимно перпендикулярны, величина
взаимно перпендикулярны, величина 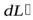 равна
равна
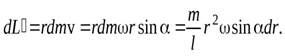
Интегрируя это уравнение
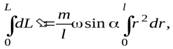
найдем величину момента импульса стержня относительно точки 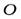
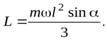
Момент импульса поворачивается вместе со стержнем, и за время 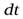 повернется на некоторый угол
повернется на некоторый угол 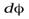 , получив приращение
, получив приращение 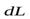 (см. рис.8). Найдем величину этого приращения
(см. рис.8). Найдем величину этого приращения
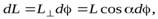

или
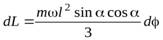 . (27)
. (27)
Подставляя уравнение (26) и (27) в уравнением моментов (25), получим
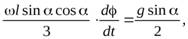
где 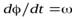 . Преобразуем это уравнение к виду
. Преобразуем это уравнение к виду
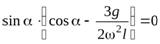 . (28)
. (28)
Если величина
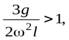
уравнение (28) имеет одно решение 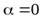 , и это положение устойчивое, т.е. стержень будет занимать вертикальное положение и будет вращаться вокруг собственной оси.
, и это положение устойчивое, т.е. стержень будет занимать вертикальное положение и будет вращаться вокруг собственной оси.
Если 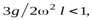 то уравнение (28) будет иметь два решение
то уравнение (28) будет иметь два решение
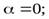 и
и 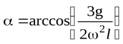 ,
,
причем можно показать, что первое решение перестает быть устойчивым, и стержень отклонится на угол, определяемый вторым решением.
б) Решим теперь задачу в неинерциальной системе отсчета, жестко связанной со стержнем. В этой системе отсчета на стержень, кроме сил взаимодействия действует центробежная сила инерции. Так как стержень находится в равновесии, сумма моментов сил, действующих на стержень, должна равняться нулю, т.е.
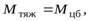
где 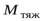 – величина момента силы тяжести,
– величина момента силы тяжести, 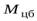 – величина момента центробежной силы инерции относительно точки
– величина момента центробежной силы инерции относительно точки 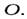 Величина момента силы тяжести определяется уравнением (26). Для нахождения момента центробежной силы инерции воспользуемся рис. 7, считая, что стержень покоится.
Величина момента силы тяжести определяется уравнением (26). Для нахождения момента центробежной силы инерции воспользуемся рис. 7, считая, что стержень покоится.
На выделенный участок стержня действует центробежная сила инерции
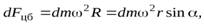
величина момента которой, относительно точки  равна
равна
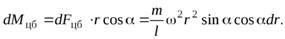
Интегрируя это выражение по всей длине стержня, получим
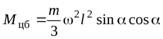 .
.
Подставляя это выражение и соотношение (26) в уравнение моментов (25), получим уравнение
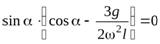 ,
,
в точности совпадающее с уравнением (28).
Надо заметить, что решение этой задачи в неинерциальной системе отсчета много проще, чем в инерциальной.
Пример 6. Однородная тонкая квадратная пластинка массы 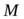 может свободно вращаться вокруг неподвижной вертикальной оси, совпадающей с одной из ее сторон. В центр пластины по нормали к ней упруго ударяется шарик массы
может свободно вращаться вокруг неподвижной вертикальной оси, совпадающей с одной из ее сторон. В центр пластины по нормали к ней упруго ударяется шарик массы 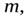 летевший со скоростью
летевший со скоростью 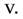 Найти величину скорости шарика
Найти величину скорости шарика 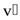 сразу после удара.
сразу после удара.
Р е ш е н и е. Система “пластина-шарик” незамкнута, так как для удержания оси пластины в неподвижном состоянии к ней необходимо приложить внешние силу. Однако надо заметить, что момент этих внешних сил относительно оси равны нулю, т.к. они приложены непосредственно к оси.
Для решения задачи воспользуемся законами сохранения энергии (удар упругий) и законом сохранения момента импульса (сумма момента внешних сил относительно оси равен нулю). Будем считать, что длина стороны пластины равна 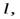 и шарик после удара будет лететь в прежнем направлении, тогда
и шарик после удара будет лететь в прежнем направлении, тогда
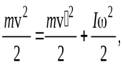
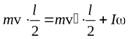 ,
,
где 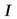 – момент инерции пластины относительно оси,
– момент инерции пластины относительно оси, 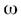 – угловая скорость, с которой пластина будет вращаться после удара вокруг оси.
– угловая скорость, с которой пластина будет вращаться после удара вокруг оси.
Для простоты решения этой системы перепишем ее в виде
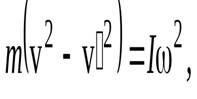
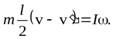 (29)
(29)
Разделив первое уравнение не второе, получим
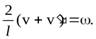 (30)
(30)
Решая совместно уравнения (29) и(30) и учитывая, что момент инерции пластины относительно оси, совпадающей с одной из ее сторон равен 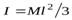 (докажите это самостоятельно), найдем скорость шарика после удара
(докажите это самостоятельно), найдем скорость шарика после удара
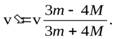
Заметим, что если 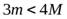 , скорость шарика после удара становится отрицательной. Это означает, что при
, скорость шарика после удара становится отрицательной. Это означает, что при 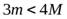 шарик полетит в обратную сторону.
шарик полетит в обратную сторону.
Пример 7. Однородный диск радиуса  и массы
и массы 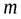 лежит на гладкой горизонтальной поверхности. На боковую поверхность диска плотно намотана нить, к свободному концу
лежит на гладкой горизонтальной поверхности. На боковую поверхность диска плотно намотана нить, к свободному концу 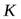 которой приложили постоянную горизонтальную силу
которой приложили постоянную горизонтальную силу 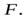 После начала движения диска точка
После начала движения диска точка 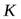 переместилась на расстояние
переместилась на расстояние 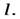 Найти угловую скорость диска к этому моменту времени.
Найти угловую скорость диска к этому моменту времени.
Р е ш е н и е. Под действием силы 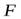 диск будет совершать плоское движение. Свяжем подвижную систему отсчета с центром масс диска. Величину ускорения центра масс
диск будет совершать плоское движение. Свяжем подвижную систему отсчета с центром масс диска. Величину ускорения центра масс 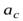 найдем из второго закона Ньютона, записанного в проекции на направление движения
найдем из второго закона Ньютона, записанного в проекции на направление движения
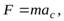
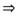
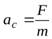 . (31)
. (31)
В системе отсчета, связанной с центром масс, диск вращается с угловым ускорением 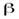 , которое найдем из уравнения вращательного движения диска
, которое найдем из уравнения вращательного движения диска
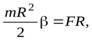
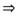
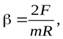 (32)
(32)
где 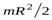 – момент инерции диска, относительно оси вращения.
– момент инерции диска, относительно оси вращения.
Найдем величины скорости 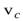 центра масс диска и угловой скорости его вращения к моменту времени
центра масс диска и угловой скорости его вращения к моменту времени 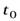 , когда точка приложения силы
, когда точка приложения силы 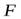 совершит перемещение
совершит перемещение 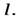 Так как в начальный момент времени диск покоился, а величины ускорений
Так как в начальный момент времени диск покоился, а величины ускорений 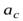 и
и 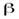 не меняются с течением времени (см. уравнения (31) и (32)), получим
не меняются с течением времени (см. уравнения (31) и (32)), получим
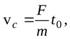
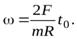
Исключаяиз этих уравнений время 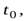 найдем связь между скоростью центра масс и угловой скоростью вращения диска
найдем связь между скоростью центра масс и угловой скоростью вращения диска
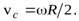 (33)
(33)
Запишем теорему об изменении кинетической энергии для диска
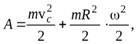 (34)
(34)
где 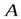 – работа всех сил, действующих на диск. Силы тяжести и сила реакции опоры работу на совершают, работу совершает только постоянная сила
– работа всех сил, действующих на диск. Силы тяжести и сила реакции опоры работу на совершают, работу совершает только постоянная сила 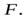 По определению работа постоянной силы равна произведению модуля силы на перемещение точки приложения силы, таким образом
По определению работа постоянной силы равна произведению модуля силы на перемещение точки приложения силы, таким образом
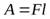 . (35)
. (35)
Подставляя выражения (33) и (35) в уравнение (34), найдем величину угловой скорости диска к моменту времени, когда точка приложения силы совершит перемещение 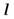
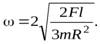
Задачи для самостоятельного решения
Задача 1. Найти момент инерции:
а) тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня 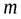 и его длина равна
и его длина равна 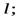
б) тонкой однородной прямоугольной пластины относительно оси, проходящей через одну из вершин пластины перпендикулярно к ее плоскости, если масса пластины 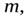 а ее стороны равны
а ее стороны равны 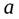 и
и 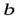 . Решить эту часть задачи прямым вычислением момента инерции и с помощью соотношения (6).
. Решить эту часть задачи прямым вычислением момента инерции и с помощью соотношения (6).
О т в е т. а) 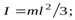 б)
б) 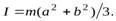
Задача 2. Тонкий однородный стержень  массы
массы 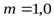 кг движется поступательно с ускорением
кг движется поступательно с ускорением 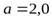
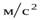 под действием двух
под действием двух
сил 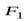 и
и 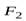 (рис. 9). Расстояние между точками приложения этих сил
(рис. 9). Расстояние между точками приложения этих сил 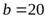 см. Кроме того, известно, что
см. Кроме того, известно, что 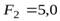 Н. Найти длину стержня.
Н. Найти длину стержня.
О т в е т. 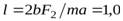 м.
м.
Задача 3. В установке, показанной на рис. 10, известны масса однородного сплошного цилиндра 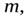 его радиус
его радиус 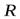 и массы тел
и массы тел 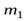 и
и 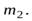 Скольжения нити и трения в оси цилиндра нет. Найти угловое ускорение цилиндра.
Скольжения нити и трения в оси цилиндра нет. Найти угловое ускорение цилиндра.
О  т в е т.
т в е т. 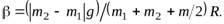
Задача 4. Однородный диск радиуса 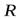 раскрутили до угловойскорости
раскрутили до угловойскорости 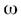 и осторожно положили плашмя на горизонтальную поверхность. Сколько времени диск будет вращаться на поверхности, если коэффициент трения равен
и осторожно положили плашмя на горизонтальную поверхность. Сколько времени диск будет вращаться на поверхности, если коэффициент трения равен 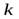 ?
?
О т в е т. 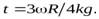
Задача 5. Гладкий однородный стержень 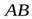 массы
массы 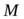 и длины
и длины 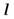
Свободно вращается с угловой скоростью 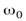 в горизонтальной плоскости вокруг неподвижной вертикальной оси, проходящей через его конец
в горизонтальной плоскости вокруг неподвижной вертикальной оси, проходящей через его конец 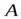 . Из точки
. Из точки 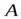 начинается скользить по стержню небольшая муфта массы
начинается скользить по стержню небольшая муфта массы 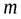 . Найти скорость
. Найти скорость 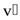 муфты относительно стержня в тот момент, когда она достигнет его конца.
муфты относительно стержня в тот момент, когда она достигнет его конца.
О т в е т. 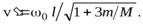
Задача 6. Вертикально расположенный однородный стержень массы 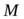 и длины
и длины 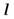 может вращаться вокруг своего верхнего конца. В нижний конец стержня попала, застряв, горизонтально летевшая пуля массы
может вращаться вокруг своего верхнего конца. В нижний конец стержня попала, застряв, горизонтально летевшая пуля массы 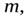 в результате чего стержень отклонился на угол
в результате чего стержень отклонился на угол 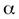 . Считая
. Считая 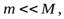 найти:
найти:
а) скорость летевшей пули;
б) приращение импульса системы “пуля-стержень” за время удара, какова причина изменения этого импульса?
в) на какое расстояние 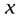 от верхнего конца стержня должна попасть пуля, чтобы импульс системы “пуля-стержень” не изменился в процессе удара.
от верхнего конца стержня должна попасть пуля, чтобы импульс системы “пуля-стержень” не изменился в процессе удара.
О т в е т. а) 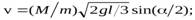 б)
б) 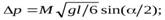
б) 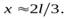
Задача 7. Два горизонтальных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны 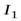
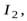 а угловые скорости –
а угловые скорости – 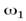 и
и 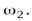 После падения вертикального диска на нижний оба диска благодаря трению между ними начали через некоторое время вращаться как единое целое. Найти:
После падения вертикального диска на нижний оба диска благодаря трению между ними начали через некоторое время вращаться как единое целое. Найти:
а) установившуюся угловую скорость;
б) работу, которую совершили при этом силы трения.
О т в е т. 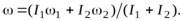
Задача 8. Однородный цилиндр массы 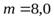 кг и радиуса
кг и радиуса 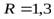 см (рис. 11) в момент
см (рис. 11) в момент 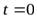 начинает опускаться под действием силы тяжести. Пренебрегая массой нити, найти:
начинает опускаться под действием силы тяжести. Пренебрегая массой нити, найти:
а) угловое ускорение цилиндра;
б) зависимость от времени мгновенной мощности, которую развивает сила  тяжести.
тяжести.
О т в е т. а) 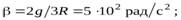 б)
б) 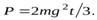
Задача 9. Однородный сплошной цилиндр массы 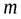 лежит на двух горизонтальных брусьях. На цилиндр намотана нить, за свешивающийся конец которой тянут с постоянной вертикально направленной силой
лежит на двух горизонтальных брусьях. На цилиндр намотана нить, за свешивающийся конец которой тянут с постоянной вертикально направленной силой 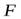 (см. рис. 12). Найти значения силы
(см. рис. 12). Найти значения силы 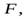 при которых цилиндр будет катиться без скольжения, если коэффициент трения равен
при которых цилиндр будет катиться без скольжения, если коэффициент трения равен 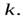
О т в е т. 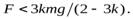
Задача 10. На гладкой горизонтальной поверхности лежит однородный стержень массы 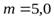 кг и длины
кг и длины 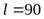 см. По одному из концов стержня в горизонтальном направлении, перпендикулярном к стержню, произвели удар, импульс силы которого
см. По одному из концов стержня в горизонтальном направлении, перпендикулярном к стержню, произвели удар, импульс силы которого 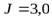
 Найти силу, с которой одна половина стержня будет действовать на другую в процессе движения.
Найти силу, с которой одна половина стержня будет действовать на другую в процессе движения.
О т в е т. 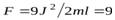 Н.
Н.
 2017-12-14
2017-12-14 3794
3794