2017-12-14
584
Экспериментальная установка (рис. 2) представляет собой металлический диск с четырьмя маленькими отверстиями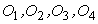 
. Диск может вращаться с малым трением вокруг оси О. Отверстия 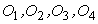расположены на взаимно перпендикулярных диаметрах. Центры отверстий находятся на одинаковых расстояниях S от оси вращения. В этих отверстиях могут крепиться грузы (цилиндры), каждый массой 
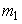. Диаметр цилиндров мал по сравнению с расстоянием S и поэтому момент инерции цилиндров можно определять по формуле момента инерции для материальной точки.
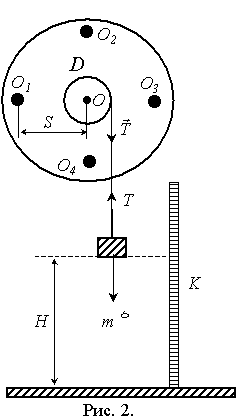На одном валу с диском находится шкив D (диаметром d), на который наматывается нить. К концу нити прикреплен груз с массой т. Подвешенный на нити груз опускается вдоль вертикальной шкалы К и приводит диск во вращательное движение. По шкале К определяется высота Н, с которой опускается груз. Время прохождения грузом т расстояния Н определяется секундомером.
Задачей данной работы является экспериментальное определение момента инерции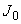 
четырех тел 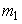, закрепленных в отверстиях 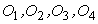. Это можно сделать, определив момент инерции диска со шкивом 
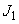и момент инерции диска со шкивом и четырьмя цилиндрами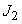 
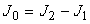. (10)
Момент инерции 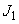можно определить следующим образом. Под действием натяжения нити Т диск начинает вращаться и масса т начинает двигаться с ускорением а. По второму закону Ньютона
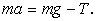(11)
Ввиду симметричности диска сумма моментов сил тяжести равна нулю. Моментом силы трения из-за его малости пренебрегаем. Тогда на шкив будет действовать только сила натяжения нити
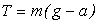. (12)
Вращающий момент, создаваемый силой Т, равен
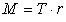, (13)
где r - радиус шкива.
Согласно основному уравнению динамики вращательного движения (9)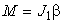 
, где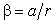 
. Следовательно, 
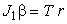или с учетом (12)
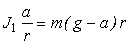
| . | (14) |
Из (14) находим
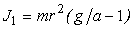
| , | (15) |
где m, r и g - величины постоянные.
Так как момент инерции 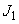данной системы есть величина постоянная, то, следовательно, ускорение а также является постоянным и его можно определить из уравнения равноускоренного движения
| , |
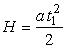
где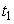 
- время движения груза т с высоты Н до пола.
Подставляя значение а из (16) в (15), получим
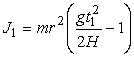
| . | (17) |
Подставив в (17)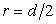 
, получим
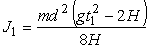
| . | (18) |
Выражение (18) определяет момент инерции диска со шкивом без грузов .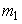
Теперь укрепим грузы 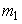на диске. Момент инерции 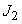будет больше чем 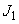, что будет заметно по увеличению времени 
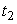движения груза т с высоты Н (при условии 
)
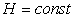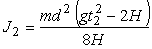
| . | (19) |
Подставляя в выражение (10) значения 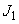и 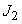из (18) и (19), получим расчетную формулу
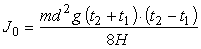
| . | (20) |
Грузы 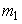представляют собой цилиндры, диаметр которых значительно меньше радиуса S. Следовательно, в данной задаче грузы 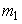можно рассматривать как материальные точки, для которых момент инерции, в соответствии с теоретической формулой, равен
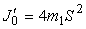
| . | (21) |
