Уравнение динамики вращательного движения твердого тела

Моментом силы относительно неподвижной точки O называется псевдовекторная величина равная векторному произведению радиус-вектора 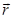, проведенному из точки O в точку приложения силы, на силу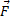

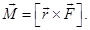
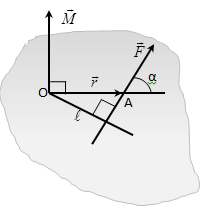
Модуль момента силы:

- псевдовектор, его направление совпадает с направлением плоскости движения правого винта при его вращении от 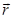к . Направление момента силы можно также определить по правилу левой руки: четыре пальца левой руки поставить по направлению первого сомножителя 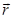, второй сомножитель входит в ладонь, отогнутый под прямым углом большой палец укажет направления момента силы . 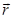Вектор момента силы всегда перпендикулярен плоскости, в котоой лежат векторы и .

-где кратчайшее расстояния между линией действия силы и точкой О называется плечом силы.

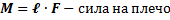
Моментом силы относительно неподвижной оси Z называется скалярная величина равнаяпроекции на эту ось вектора момента силы , определённого относительно произвольной точки O данной оси Z. Если ось Z перпендикулярна плоскости, в которой лежат векторы и 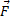, т.е. совпадает с направлением вектора , то момент силы представляется в виде вектора совпадающего с осью.

Ось, положение которой в пространстве остается неизменнымпривращении вокруг тела в отсутствие внешних сил,называется свободной осью тела.

Для тела любой формы и с произвольным распределением массы существует 3 взаимно перпендикулярных, проходящих через центр инерции тела оси, которые могут служить свободными осями:они называются главными осями инерции тела.

Найдем выражение для работы при вращательном движении тела. Пусть на массу m твердого тела действует внешняя сила . Тогда работа этой силы за время d t равна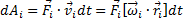

Осуществим в смешанном произведении векторов циклическую перестановку сомножителей, воспользовавшись правилом

Тогда

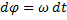
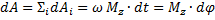
Работа при вращении тела равна произведению момента действия силы на угол поворота . Работа при вращении тела идет на увеличение его кинетической энергии:

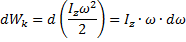
Поэтому

или

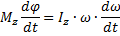
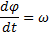
Следовательно,

- уравнение динамики вращательного движения

Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то выполняется векторное равенство

І - главный момент инерции (момент инерции относительно главной оси)