Преобразования формулы для любого члена бесконечной арифметической прогрессии

1. Если к нулевому члену прибавить или отнять разность прогрессии , то от этого прогрессия не изменится, а только переместится нулевой член, т.е. изменится нумерация членов.

2. Если коэффициент при переменной величине умножить на , то от этого произойдет лишь перестановка правой и левой групп членов.

3. Если последовательных членов бесконечной прогрессии

например , , ,..., , сделать центральными членами прогрессий с одинаковой разностью, равной :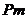

то прогрессия и ряд прогрессий выражают собой одни и те же числа.

Пример Ряд может быть заменен следующими тремя рядами: , , .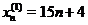

4. Если бесконечных прогрессий с одинаковой разностью имеют центральными членами числа, образующие арифметическую прогрессию с разностью , то эти рядов могут быть заменены одной прогрессией с разностью , и с центральным членом, равным любому из центральных членов данных прогрессий, т.е. если

то эти прогрессий объединяются в одну:

Пример , , , обе объединяются в одну группу , так как .

Для преобразования групп, имеющих общие решения, в группы, общих решений не имеющие данные группы разлагают на группы с общим периодом, а затем стремяться объединить получившиеся группы, исключив повторяющиеся.