2017-12-14
2283
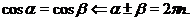
Пример Решить уравнение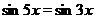 
.
Решение.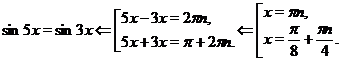 
Ответ. 
, 
.
Пример Решить уравнение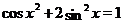 
.
Решение. Преобразуем уравнение. 
Ответ.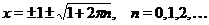 
.
Пример Известно, что 
и 
удовлетворяют уравнению
Найти сумму 
.
Решение. Из уравнения следует, что
Ответ. 
1.10 Домножение на некоторую тригонометрическую функцию
Рассмотрим суммы вида
Данные суммы можно преобразовать в произведение, домножив и разделив их на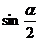 
, тогда получим
Указанный прием может быть использован при решении некоторых тригонометрических уравнений, однако следует иметь в виду, что в результате возможно появление посторонних корней. Приведем обобщение данных формул:
Пример Решить уравнение 
.
Решение. Видно, что множество 
является решением исходного уравнения. Поэтому умножение левой и правой части уравнения на 
не приведет к появлению лишних корней.
Имеем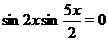 
.
Ответ. 
; 
.
Пример Решить уравнение 
.
Решение. Домножим левую и правую части уравнения на и применив формулы преобразования произведения тригонометрических функций в сумму, пролучим
Это уравнение равносильно совокупности двух уравнений 
и 
, откуда 
и 
.
Так как корни уравнения 
не являются корнями уравнения, то из полученных множеств решений следует исключить 
. Значит во множестве нужно исключить 
.
Ответ. и , 
.
Пример Решить уравнение 
.
Решение. Преобразуем выражение 
:
Уравнение запишется в виде:
Принимая 
, получаем 
. 
, 
. Следовательно
Ответ. 
.
