Действие магнитного поля на движущиеся заряды. Сила Лоренца

На заряды, движущиеся в магнитном поле, действует сила, которую называют силой Лоренца. Эта сила определяется величиной заряда q, скоростью его движения и магнитной индукцией в той точке, где находится заряд в данный момент от взаимной ориентации векторов и .Направление векторов и определяют направление силы Лоренца. Итак, сила Лоренца:

. (4.4.1)

Модуль силы Лоренца:

, (4.4.2)

где a - угол между и .

Если заряженная частица покоится ( = 0), то магнитное поле на нее не действует. Магнитное поле действует только на движущиеся в нем заряды. Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат вектора и (см. рис.20.11). Если заряд отрицательный, то сила 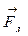имеет противоположное (указанному на рисунке) направление. Направление силы Лоренца может быть определено и с помощью правила левой руки. Так как сила Лоренца всегда направлена перпендикулярно к скорости заряженной частицы, она не совершает работы над частицей. Величина скорости и, следовательно, кинетической энергии частицы не

i ii

+Q

i i

i ii

Рис.20.11

изменяются, изменяется лишь направление скорости, т.е. заряженная частица, движущаяся в однородном магнитном поле, приобретает постоянное по величине нормальное ускорение. Итак, если частица движется в магнитном поле со скоростью вдоль линий магнитной индукции, то сила Лоренца равна нулю (угол a между векторами и равен 0 или p) и скорость частицы остается постоянной. Если же скорость перпендикулярна , то сила Лоренца постоянна по модулю и нормальна к траектории частицы и создает центростремительное ускорение (согласно второму закону Ньютона). Радиус траектории может быть определен из соотношения:

F_л = F_цс или , (4.4.3)

откуда:

. (4.4.4)

Радиус частицы зависит от скорости , магнитной индукции и удельного заряда . Определим период вращения частицы (время полного оборота), разделив длину окружности на скорость.

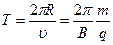, (4.4.5)

т.е. период вращения не зависит от скорости при «с, а зависит лишь от индукции магнитного поля и величины, обратной удельному заряду . Если скорость заряженной частицы ориентирована относительно вектора , произвольным образом, то следует разложить вектор начальной скорости на составляющие: параллельную магнитному полю, 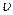₁₁и перпендикулярную к нему 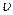^ (рис 20.12).

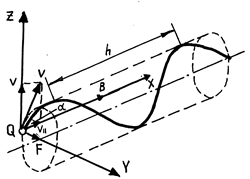Рис.20.12

Составляющая 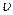₁₁ в процессе движения остается постоянной, т.к. сила Лоренца не имеет составляющей, направленной вдоль силовой линии

.

В плоскости перпендикулярной полю, частица равномерно движется по окружности со скоростью 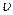^ = 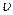sina. Радиус окружности:

.

Сложение обоих движений (равномерного перемещения вдоль направления магнитного поля и равномерного вращения в перпендикулярной плоскости) приводит к движению частицы по винтовой линии. Шаг винтовой линии:

h= 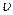₁₁ T = 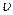Tcosa (4.4.6)

или h = 2p m 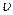cosa / (Bq). (4.4.7)

Направление, в котором закручивается спираль, зависит от знака заряда частицы. Если имеются одновременно электрическое и магнитное поля, то лоренцева сила, действующая на заряженную частицу, равна:

. (4.4.8)