Описание модели панельных данных с фиксированными эффектами

В введенных обозначениях модель панельных данных с фиксированными эффектами описывается уравнением

(1) .

Величина выражает индивидуальный эффект объекта 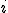, не зависящий от времени 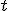, при этом регрессоры 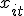не содержат константу.

Параметры модели: .

Основные предположения

Предположим, что выполнены следующие условия:

1. ошибки 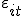некоррелированы между собой по 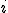и , , ;
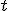2. ошибки 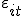некоррелированы с регрессорами при всех .

Понижение размерности. Исключение эффектов.

Для панельных данных типична ситуация, когда число объектов 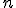достаточно велико. Поэтому, применяя непосредственно метод наименьших квадратов к уравнению (1), при оценивании параметров можно столкнуться с вычислительными проблемами. Их можно преодолеть, исключая из рассмотрения индивидуальные эффекты . При этом мы понижаем размерность задачи с до .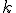

Наиболее простой способ – переход в уравнении (1) к средним по времени величинам:

(2) ,

где.

Вычитая почленно (2) из (1), получаем:

(3) .

Данная модель уже не зависит от эффектов . По существу, это уравнение (1), записанное в отклонениях от индивидуальных средних по времени.