Во введенных обозначениях модель панельных данных со случайными эффектами описывается уравнением
(1)  ,
,
где  – константа, а
– константа, а  – случайная ошибка, инвариантная по времени для каждого объекта.
– случайная ошибка, инвариантная по времени для каждого объекта.
Параметры модели:  .
.
Основные предположения:
Предположим, что выполнены следующие условия:
- ошибки
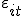 некоррелированы между собой по
некоррелированы между собой по 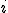 и
и 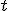 ,
,  ,
,  ;
; - ошибки
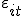 некоррелированы с регрессорами
некоррелированы с регрессорами  при всех
при всех  ;
; - ошибки
 некоррелированы между собой по
некоррелированы между собой по 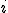 ,
,  ,
,  ;
; - ошибки
 некоррелированы с регрессорами
некоррелированы с регрессорами  при всех
при всех  :
:  ;
; - ошибки
 и
и 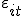 некоррелированы при всех
некоррелированы при всех  :
:  .
.
Оценка параметров модели:
Модель со случайным эффектом (1) можно рассматривать как линейную модель, в которой ошибка  имеет некоторую специальную структуру. Будем рассматривать модель:
имеет некоторую специальную структуру. Будем рассматривать модель:
(2)  .
.
Для получения оценок параметров  можно применить обычный метод наименьших квадратов. Условия 1)-3) гарантируют несмещённость и состоятельность этих оценок. Однако ошибки в (2) не являются гомоскедастичными, поэтому для построения эффективных оценок можно воспользоваться обобщенным методом наименьших квадратов.
можно применить обычный метод наименьших квадратов. Условия 1)-3) гарантируют несмещённость и состоятельность этих оценок. Однако ошибки в (2) не являются гомоскедастичными, поэтому для построения эффективных оценок можно воспользоваться обобщенным методом наименьших квадратов.
 2017-12-14
2017-12-14 542
542








