Оценка параметров парной регрессионной модели методом наименьших квадратов (суть метода, вывод формул для нахождения оценок коэффициентов через систему нормальных уравнений)

Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов. Его оценки обладают такими статистическими свойствами, как:

· Несмещенность (математическое ожидание остатков равно нулю)

· Состоятельность (увеличение точности оценок с увеличением объема выборки)

· Эффективность (оценки характеризуются наименьшей дисперсией)

Метод наименьших квадратов (МНК) дает оценки, имеющие наименьшую дисперсию в классе всех линейных оценок, если выполняются предпосылки нормальной линейной регрессионной модели. МНК минимизирует сумму квадратов отклонения наблюдаемых значений 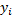от модельных значений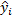

Оценки 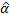, 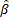находятся путем минимизации суммы квадратов

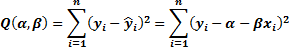
По всем возможным значениям 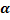и 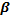при заданных (наблюдаемых) значениях 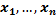, 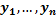. Задача сводится к математической задаче поиска точки минимума функции двух переменных. Точка минимума находится путем приравнивания к нулю частных производных функции 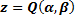по переменным 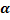и 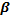. Этоприводитк системенормальныхуравнений

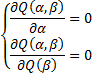
решением которой и является пара 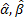. Согласно правилам вычисления производным, имеем

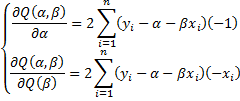
так что искомые значения 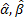удовлетворяют соотношениям

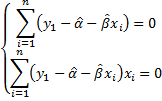
Эта система является системой двух линейных уравнений с двумя неизвестными и может быть легко решена, например, методом подстановки. В результате получаем так называемые оценкинаименьшихквадратов:

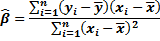
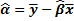
Такое решение может существовать только при выполнении условия

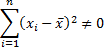
что равносильно отличию от нуля определителя системы нормальных уравнений.