2017-12-14
2322
Пусть исходное уравнение регрессии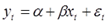 
содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется автокорреляционной схеме первого порядка: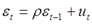 
, где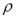 
- коэффициент автокорреляции, а 
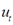- случайный член, удовлетворяющий предпосылкам МНК.
Данная схема оказывается авторегрессионой, поскольку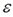 
определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно единице.
Величина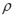 
есть коэффициент корреляции между двумя соседними ошибками. Пусть 
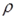известно. Преобразуем исходное уравнение регрессии следующим образом:
.
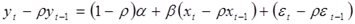Обозначим: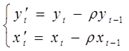 
.
Это преобразование переменных называется авторегрессионым (AR), или преобразованием Бокса-Дженкинса.
Тогда преобразованное уравнени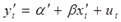е 
, где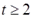 
, 
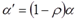, не содержит автокорреляцию, и для оценки его параметров 
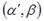используется обычный МНК.
Способ вычисления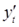 
и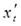 
приводит к потере первого наблюдения. Эта проблема при малых выборках обычно преодолевается с помощью поправки Прайса-Винстена:
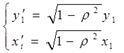
Оценка коэффициента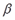 
из этой зависимости непосредственно используется и для исходного уравнения, а коэффициент рассчитывается по формуле: 
.
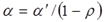На практике величина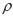 
неизвестна, ее оценка получается одновременно с оценками 
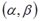в результате следующих итеративных процедур.
Способы корректировки автокорреляции: алгоритм метода Кохрейна-Оркатта.
1. По выборочным данным выполняется настройка модели, и вычисляется вектор остатков регрессии е = (e1, e2 , …, en)T.
2. По остаткам регрессии оценивается модель авторегрессии et=ρet-1+ vt
3. С оценкой параметра авторегрессии выполняются этап преобразования переменных и определения МНК – оценок вектора параметра β.
4. Строится новый вектор остатков, и процедура повторяется, начиная с п. 2. Интеграционный процесс заканчивается при условии совпадения оценок по последней и предпоследней интерациях с заданной степенью точности.
