Гидравлические элементы поперечного профиля канала

 

Каналы в зависимости от их назначения, рода грунтов, применяемых механизмов, местных условий устраиваются различной формы поперечного сечения (рис. 6.11): трапецеидальной, прямоугольной, параболической и т.д.

В системах дорожного водоотвода, в системах мелиорации и водоснабжения, в гидроэнергетике и других отраслях хозяйства наибольшее распространение получили каналы полигонального поперечного сечения, ча­ще трапецеидального (рис. 6.11, а) и прямоугольного (рис. 6.11, б) профилей. Треугольный профиль имеют лотки по­верхностного водоотвода на городских улицах (рис. 6.11, г, в).

 

Рис. 6.11.1

 

Для характеристики поперечного сечения каналов приняты следующие обозначения:

b - ширина канала по дну;

т - коэффициент откоса, равный ctg Ө, ;

Ө- угол (см. рис. 6.11.1) задается не по соображениям гидравлического расчета, а с учетом устойчивости грунта откоса; его величина зависит от рода и качества грунта, в котором устроен канал, а также от принятого способа укрепления откоса;

В - ширина потока по верху;

ω - площадь живого сечения;

χ - смоченный периметр;

R – гидравлический радиус

R = ω/χ.

Глубина и ширина канала по дну зависят от расчетной пропускной способности канала, его технического назначения и местных условий (рода грунтов, ширины полосы землеотвода под канал, уклона поверхности, вида применяемой землеройной техники и т.п./

Живое сечение трапецеидальных каналов при произволь­ной глубине потока h, ширине по дну b и заложениях от­косов m=ctg Ө₁=a₁/h и m₂=ctg Ө₂=a₂/h характеризует­ся следующими параметрами:

площадью живого сечения

(6.24)

смоченным периметром

(6.25)

шириной потока по свободной поверхности

B = b + (m₁ + m₂)h. (6.26)

Формулы (6.24)-(6.26) при симметричном трапецеидальном профиле (m₁=m₂) упрощаются

ω = (b + mh)h; В = b + 2 mh.

Прямоугольные и треуголь­ные сечения каналов представляют частные случаи трапе­цеидального.

В частности, для прямоугольного профиля m₁= m₂=0, отсюда

B = b; m = ctg 90^o = 0; ω = bh; χ = b + 2h.

Для треугольного профиля b=0, отсюда

ω = mh²; B = 2mh.

Каналы (лотки) криволинейного поперечного сечения встречаются реже. Например, в оросительных системах находят применение лотки параболического профиля (рис. 6.11.1, а), описываемого обычно уравнением квадратичной параболы

ω = 2/3 bh.

На дорогах иног­да используются также лотки полукруглого профиля (рис. 6.11.2, б).

Рис. 6.11.2

 

Прочие поперечные сечения, встречающиеся в практике, показаны на рис. 6.12:

а) несимметричные профили (рис. 6.12, а); на рисунке показано русло, которое характеризуется еще тем, что величина коэффициента шероховатости n различна для разных участков смоченного периметра ;

б) неправильные профили (рис. 6.12, б); в этом случае, как и в предыдущем, величины ω и χ приходится вычислять, разбивая поперечное сечение канала на отдельные части;

в) составные профили (рис. 6.12, в );

г) замкнутьe профили (рис. 6.12, г); здесь имеем так называемый закрытый канал.

В случае весьма широких русел всегда можно считать, что

 

 

Рис. 6.12

Трубы кругового или иного профиля при их работе с час­тичным наполнением представляют собой замкнутыe профили (рис. 6.12, г); здесь имеем так называемый закрытый канал, расчет которых рассмотрен ниже.

 

Основные зависимости для расчета равномерного дви­жения в призматических руслах

 

Выведем уравнение равномерного движения жидкости применительно к турбулентному режиму, наиболее часто встречающемуся на практике.

Рассмотрим равномерное напорное движение жидкости в цилиндрической трубе с площадью живого сечения w. Сечениями 1 - 1 и 2 - 2 выделим участок потока длиной L и отнесем его к произвольно выбранной плоскости сравнения О - О. Падение пьезометрической линии P - P в пределах выделенного участка выражает собой потерю напора h_f на трение по длине L (рис.1 - 1).

 

 

Из определения равномерного движения следует, что ускорения, а следовательно и силы инерции, равны нулю. Поэтому сумма проекций на любую ось всех внешних сил, приложенных к выделенному объему жидкости, должна быть равна нулю. Спроектируем эти силы на ось X - Х, совпадающую с направлением движения потока жидкости.

К внешним силам, действующим на выделенный объем жидкости, относятся

- сила тяжести, направленная вертикально вниз, и равная весу выделенного объема жидкости G = g.w..L.. Проекция этой силы на ось X – X G_x = G.sina;

- силы P₁ и P₂, давления на торцевые сечения выделенного участка потока со стороны жидкости, расположенной до сечения 1 - 1 и за сечением 2 - 2

P₁ = p₁.w; P₂ = p₂.w,

где p₁ и p₂ – гидродинамические давления в центре живых сечений (в т.т. 1 и 2).

Силы P₁ и P₂ проектируются на ось X – X без искажения, причем сила P₁ направлена в сторону движения жидкости, а сила P₂ – в противоположную сторону. Равнодействующая этих сил

P₁ - P₂ = (p₁ – p₂).w;

- силы давления стенок трубы на боковую поверхность выделенного объема жидкости – нормальные к этой поверхности. Проекции этих сил на направление движения равны нулю;

- силы сопротивления, обусловленные трением потока о стенки. Обозначив силу трения, приходящуюся на единицу поверхности соприкосновения потока со стенками, (иначе говоря касательное напряжение ”на стенке”) через t_о, вычислим величину силы трения T в пределах выделенного отсека жидкости по формуле

T = t_o.c.L,

где c - смоченный периметр.

Составив сумму проекций всех внешних сил на направление движения и приравняв ее нулю, получим:

G.sin a + P₁ – P₂ – T = 0

Учитывая ранее приведенные выражения для действующих сил, а также выражение (см. рис. 1 – 1), уравнение равновесия рассматриваемого объема жидкости можно представить так

g.w.(z₁ – z₂) +w.(p₁ – p₂) -t_o.c.L = 0. (1 – 1)

Поделив все члены уравнения (1 – 1) на вес жидкости g.w.L и группируя все слагаемые с одинаковыми индексами, получим:

(1 – 2)

В левой части этого равенства имеем выражение пьезометрического уклона I_p при равномерном движении. Правую часть равенства (1 – 2) можно упростить, учитывая, что 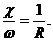Тогда из равенства (1 – 2) будем иметь:

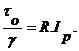(1 – 3)

Теоретическими и экспериментальными исследованиями установлено, что при вполне развитом турбулентном движении (в квадратичной зоне сопротивлений) касательные напряжения пропорциональны квадрату скорости, т.е. , где y - некоторый коэффициент пропорциональности. Подставив выражение для t_о в равенство (1 – 3), получим , откуда . Обозначив , расчетную зависимость для определения средней скорости равномерного напорного движения жидкости получим в следующем виде

, (1 – 4)

а для определения расхода жидкости – в виде:

. (1 – 5)

Зависимости (1 – 4) и (1 – 5) представляют собой две формы выражения расчетного уравнения равномерного напорного движения жидкости при турбулентном режиме. Для равномерного безнапорного движения жидкости, когда гидравлический уклон равен уклону дна канала, уравнение равномерного движения примет вид:

, (1 – 6)

или

. (1 – 7)

Коэффициент С, входящий в уравнения напорного и безнапорного движения жидкости при турбулентном режиме, имеет размерность корня квадратного из ускорения, т.е.

.

Уравнение равномерного движения жидкости было впервые получено Шези (Chezy) в 1775 г. и поэтому известно в литературе как формула Шези, а коэффициент С – как коэффициент Шези. В отличие от Шези, полагавшего значение коэффициента С постоянным, более поздними исследованиями было установлено, что коэффициент С изменяется в широких пределах и зависит от геометрических размеров потока (гидравлического радиуса) и шероховатости стенок труб или каналов (характеризуемой коэффициентом шероховатости n).

В качестве основной зависимости для определения коэффициента С используется формула Н.Н.Павловского

, (1 – 8)

где у - показатель степени, зависящий в свою очередь от гидравлического радиуса R и коэффициента шероховатости n, т.е. y = y(R, n).

В некоторых гидравлических расчетах (в частности при расчете дорожных труб) для определения коэффициента С используется формула Маннинга

. (1 – 9)

 

Формула Шези

 

Основной зависимостью для расчета равномерного дви­жения в призматических руслах является формула Шези

Применительно к открытым равномерным потокам с нормальной глубиной, где

Q = ωv = const (вдоль потока),

а, также учитывая формулу (6.23), формулу Шези можно представить в виде

(6.27)

или

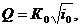
где расходную характеристику (модуль расхода К_о) нахо­дят по зависимости

(6.28)

Входящие в формулу (6.27) геометрические характеристики живого сечения ω₀, χ₀, R₀ и коэффициент Шези С₀ соответст­вуют глубине равномерного потока h₀.

Определение коэффициентов Шези для открытых русл.

Коэффициент Шези определяется в зависимости от режима движения и области сопротивле­ния либо только числом Рейнольдса, либо только относи­тельной шероховатостью смоченной поверхности русла, либо обоими этими факторами в совокупности. (Последние исследования показали, что коэффициенты С и λ зависят также и от формы русла).

Открытые каналы, а также каналы замкнутого профиля (коллекторы, гидротехнические туннели, дорожные и ме­лиоративные трубчатые сооружения) имеют значительную шероховатость. Движение жидкости в них происходит пре­имущественно в области квадратичного сопротивления. В некоторых случаях, например в лотках систем водоотво­да, на покрытиях улиц, дорог движение жид­кости может соответствовать области доквадратичного со­противления, гладких русл и даже области ламинарного движения.

Для области квадратичного сопротивления предложе­ны одночленные, показательные и многочленные формулы. В инженерной практике наиболее распространены формулы двух последних типов. Из показательных наиболее извест­на формула Павловского. Широко применяются при рас­четах также формулы Маннинга, многочленная формула Агроскина (табл. 6.1).

Таблица 6.1

Расчетные формулы для определения коэффициента Шези

Особое положение занимает приведенная в табл. 6.1 обобщенная формула Альтшуля, рекомендованная им для определения коэффициента Шези в области квадратичного и доквадратичного сопротивлений, а также в области гид­равлически гладких русл.

Для русла прямоугольного профиля конечной ширины значения С несколько меньше, чем вычисленные по форму­ле Так, например, для русла с размером b= 2h₀ разница составляет 8%. Таким образом, эта форму­ла годится для расчетов с достаточной для практических случаев точностью для области ламинарного режима.

 

Гидравлически наивыгоднейшее сечение трапецеидального канала

 

Каналы, сечение которых при неизменной площади ω₀ характеризуется наименьшим значением смо­ченного периметра χ_min и, следовательно, наибольшим зна­чением гидравлического радиуса R _max= ω₀ / χ_min согласно формуле Шези (6.27), обладают наибольшей пропускной способностью при равномерном движении. Такое сечение канала называется гидравлически наивыгод­нейшим. Оно также может быть определено как сече­ние с наименьшей площадью ω₀ и наибольшей средней ско­ростью течения v при заданных величинах i₀, n, Q.

Т.о. гидравлически наивыгоднейшим сечением канала называется такое его поперечное сечение, которое при заданной площади ω и уклоне i имеет наибольшую пропускную способность.

Известно, что при заданной площади наименьший пери­метр имеет круг (или полукруг). Таким образом, каналы полукруглого профиля являются гидравлически наивыгод­нейшими. Гидравлический радиус таких каналов

Очевидно, что каналы с иной формой поперечного сечения, например прямоугольной, трапецеидальной и др., имеют гидравлически наивыгоднейшее сечение при опре­деленных соотношениях β_ГН=(b/h₀)_ГН. Если площадь жи­вого сечения ω и смоченный периметр χ выразить через соотношение blh, величина β_ГН может быть определена из условия

(6.36)

поскольку для канала с гидравлически наивыгоднейшим сечением при ω=const периметр принимает минимальное значение: χ=χ_min.

Для русла трапецеидальной формы поперечного сече­ния из формулы (6.36) имеем

(6.37)

При подстановке β_ГН в выражения (6.24) и (6.25) гидравли­ческий радиус для трапецеидального канала гидравлически наивыгоднейшего сечения равен

Зависимость β_ГН=β(m) и значения относительной шири­ны канала по свободной поверхности из выражения (6.26) представлены ниже:

т..................... 0 0,5 1,0 1,5 2,0 2,5 3,0

β_ГН.................. 2 1,236 0,828 0,606 0,472 0,385 0,325

B/h_a................ 2,0 2,236 2,828 3,606 4,472 5,385 6,325

Из этой зависимости следует, что каналы с гидравличес­ки наивыгоднейшим сечением являются относительно глу­бокими. Поэтому проектировать крупные каналы, ориенти­руясь на гидравлически наивыгоднейшее сечение, не всегда экономически целесообразно. Например, у прямоуголь­ного судоходного канала шириной b= 100 м при β_ГН =2 глубина h₀=50 м. Глубина же канала в этом случае долж­на назначаться исходя из осадки судов. Строительство и последующая эксплуатация относительно глубоких каналов с гидравлически наивыгоднейшим сечением часто зат­руднительны. В таких случаях приходится несколько откло­няться от указанных выше значений β_ГН.

Малые каналы дорожного и аэродромного водоотвода, мелиоративные и т. д. целесообразно проектировать с гидравлически наивыгоднейшим сечением.