Индукция поля прямого бесконечного проводника с током

Р
ассматривается отрезок прямого провода 1-2 с током I (рис.14.5). Элемент тока 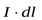создаёт в точке А поле, индукцию которого можно записать по закону Био-Савара-Лапласа:

.

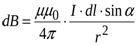Вектор направлен на нас из-за рисунка. Любой другой элемент тока того же проводника создаёт в точке А индукцию, направленную так же. Тогда вместо векторов в (14.7) можно интегрировать модуль; а пределы интегрирования – точки 1 и 2, начало и конец провода:

. (14.9)

Из рис.14.5 получим:

, (14.10)

а длина отрезка СD равна:

. (14.11)

Последнее соотношение подставим в (14.9) и заменим из (14.10):

;

.

.

Окончательно получим, что индукция отрезка прямого проводника на расстоянии d от него равна:

. (14.12)

Частный случай – проводник бесконечен; тогда углы , , и

.

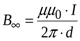. (14.13)

^ 3.2. Индукция в центре кругового тока

Любой элемент тока создаёт в центре витка (рис.14.6) индукцию , направленную одинаково (вверх, по правилу буравчика); тогда векторный принцип суперпозиции (14.7) сводится к скалярному интегралу по окружности:

.

По закону Био-Савара-Лапласа:

,

т огда

;

Окончательно, индукция в центре кругового тока индукция равна:

. (14.14)

 

^ 3.3. Индукция на оси кругового тока

Найдём индукцию на оси кругового тока в точке А на высоте h над плоскостью витка (рис.14.7). Элемент тока 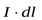создаёт индукцию , направленную перпендикулярно радиус-вектору точки А и элементу тока 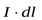. Из соображений симметрии понятно, что результирующая индукция направлена по оси симметрии тока – оси OY, и она равна собственной проекции на ось OY:

;

причём . Дальше по закону Био-Савара-Лапласа:

,

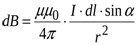где , .

Тогда

.

Окончательно:

. (14.15)

^ 3.4. Поле соленоида

Соленоид – это катушка провода, намотанная на цилиндрический каркас (рис.14.8). Будем считать, что диаметр провода мал по сравнению с диаметром самого соленоида, и витки вплотную прилегают друг к другу. По обмотке соленоида течёт ток I. Индукцию магнитного поля в произвольной точке А на оси соленоида можно рассчитать по формуле (14.16):

, (14.16)

где – плотность намотки соленоида (число витков на единицу длины; N – полное число витков соленоида длиной l); углы 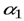и – см. рис.14.9.

Доказательство (14.15) дано в лаб. работе 2-12.

Если соленоид достаточно длинный (бесконечный), то углы

, ;

, ;

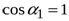тогда

.

Окончательно получим:

. (14.17)

Вектор индукции направлен по оси соленоида по правилу буравчика.

^ 3.5. Поле движущегося заряда

Движущаяся заряженная частица (рис.14.10) тоже создаёт магнитное поле. Индукцию его можно получить из закона Био-Савара-Лапласа, если сделать замену:

Такую замену можно обосновать тем, что сам движущийся заряд создаёт некоторый эквивалентный электрический ток, и по размерности величины и совпадают:

Итак, индукция магнитного поля, созданного движущимся со скоростью зарядом q в точке А с радиус-вектором , равна:

; (14.18)

(14.18а)

и направлена по правилу буравчика по касательной к окружности, охватывающей воображаемый проводник – траекторию заряда (если заряд положительный. Если отрицательный, то эквивалентный ток направлен противоположно скорости, и направление индукции тоже надо сменить на противоположное.)

^ 4. Закон полного тока для магнитного поля в вакууме. Непотенциальность магнитного поля

Напоминание: циркуляция любого векторного поля (например, вектора магнитной индукции ) – это интеграл по замкнутому контуру L:

,

где – угол между направлением вектора и элементом длины контура , B_l – проекция на элемент длины контура (касательная составляющая), рис.14.11. Направление обхода контура связано с направлением нормали 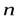к нему правилом буравчика.

Теорема о циркуляции (закон полного тока): циркуляция вектора магнитной индукции для поля в вакууме по произвольному замкнутому контуру равна алгебраической сумме токов, охваченных контуром, умноженной на магнитную постоянную .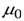

. (14.19)

Правило знаков: если ток пронизывает контур в направлении нормали к контуру, то в сумме (14.19) ток берём со знаком «+»; иначе – «–».

Пример: рис.14.12.

.

Если задана плотность тока в любой точке поверхности, натянутой на контур L, то теорема о циркуляции выглядит так:

. (14.19а)

Интеграл в правой части берётся по любой поверхности, натянутой на контур L.

Применение закона полного тока для расчёта полей

Пример1.

Поле прямого бесконечного провода на расстоянии R от него (рис.14.13). Индукция в любой точке контура L направлена по касательной к контуру и в силу симметрии одинакова, тогда циркуляция равна:

,

отсюда

,

,

что совпадает с (14.13) для поля в вакууме.

Пример2.

Поле длинного (бесконечного) соленоида.

П
оле внутри соленоида однородно, а вне соленоида практически равно нулю (если соленоид достаточно длинный). Контур выбираем в виде узкого длинного прямоугольника, одна длинная сторона которого находится внутри соленоида параллельно его оси, а вторая – вне его (рис.14.14). Вклад в циркуляцию интегралов по внешней стороне и коротким сторонам прямоугольника мал, тогда

.

Ток I пронизывает контур N раз, тогда

,

,

,

где – плотность намотки соленоида. Полученный результат совпадает с (14.17).

Магнитное поле непотенциально, так как циркуляция вектора магнитной индукции по замкнутому контуру в общем случае не равна нулю:

.

Магнитное поле носит вихревой характер. Линии магнитной индукции замкнуты; на рис. 14.15 изображено поле прямого тока, кругового витка, соленоида и полосового магнита.

 

^ 5. Действие магнитного поля для движущиеся заряды и токи

5 .1. Сила Лоренца

На заряд, движущийся в магнитном поле, действует сила Лоренца:

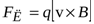. (14.20)

Направление силы Лоренца можно найти по правилу буравчика: вектор скорости поворачиваем по ближайшему углу к вектору ; поступательное движение буравчика даёт направление . Если знаете правила векторного произведения, школьное правило левой руки помнить необязательно. По этому правилу четыре пальца левой ладони нужно направить по скорости, а линии индукции должны входить в ладонь, тогда большой палец покажет направление силы Лоренца (рис.14.16). Так работает правило левой руки в случае положительного заряда; если же заряд отрицателен, нужно направление силы сменить на противоположное. Величина силы Лоренца равна

, (14.21)

г
де – угол между скоростью и полем. На рис.14.17, а сила Лоренца направлена от нас за рисунок.

Сила Лоренца перпендикулярна как индукции поля (), так и скорости частицы (); последнее означает, что она не совершает работы, так как не имеет касательной составляющей к траектории:

.

Сила Лоренца действует только на движущиеся заряды.

^ 5.1.1. Движение заряженной частицы в магнитном поле под действием силы Лоренца

П
усть положительно заряженная частица влетает в однородное магнитное поле под углом α к направлению линий индукции (рис.14.18).

Величина силы равна . Скорость v частицы можно разложить на две составляющие: одна перпендикулярна направлению поля, другая параллельна: ; . Тогда можно представить силу Лоренца как . Движение частицы является суперпозицией двух движений: вращение по окружности радиуса R со скоростью в плоскости, перпендикулярной полю, и равномерное поступательное движение вдоль линий поля со скоростью ; в результате получается движение по винтовой линии с шагом (расстоянием между соседними витками), равным , где – период вращения. По второму закону Ньютона , или . Отсюда ; ; .

^ 5.1.2. Магнетизм – релятивистский эффект

Полная сила, действующая на заряженную частицу в электромагнитном поле, равна

. (14.22)

Это – формула Лоренца. Первое слагаемое – привычная нам сила Лоренца – это магнитная составляющая полной силы, действующей на частицу в электромагнитном поле; второе – электрическая составляющая.

;

.

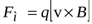Как уже было сказано, сила Лоренца 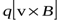действует только на движущиеся заряды. А что будет происходить, если перейти в систему отсчёта, связанную с частицей, в которой она неподвижна? Ведь тогда сила Лоренца действовать перестанет, а сила не может исчезнуть, если мы перешли к другой системе отсчёта.

Дело в том, что поля – электрическое и магнитное – неразрывно связаны. При переходе к другой системе отсчёта полная сила (14.22) останется прежней; изменится всего лишь наше её объяснение.

Конкретный пример:

По проводнику течёт ток; электроны движутся направленно со скоростью . Параллельно проводнику с той же скоростью летит электрон. Ток создаёт магнитное поле, направленное на нас, и на электрон действует сила Лоренца, направленная к проводнику (рис. 14.19).

В системе отсчёта, связанной с электроном, магнитная составляющая силы Лоренца не действует, так как электрон покоится. Сила не исчезла; это – электрическая составляющая силы Лоренца: проводник оказался заряжен положительно в этой системе отсчёта из-за релятивистского сокращения его длины, поскольку он сам в этой системе движется со скоростью v:

.

В результате объём его уменьшился, концентрация положительных ионов увеличилась и не компенсируется отрицательным зарядом электронов.

Можно количественно доказать, что обе силы в обеих системах отсчёта одинаковы. Сила не исчезла, изменилось лишь наше её описание: в одной системе отсчёта на электрон действовало магнитное поле тока, в другой – электрическое поле заряженного проводника. Нет отдельно поля только электрического или только магнитного; есть единое электромагнитное поле. В одной системе отсчёта это поле может выглядеть как только магнитное; в другой – как электрическое; в третьей присутствует и магнитное, и электрическое.

Существуют формулы преобразования векторов и при переходе из одной системы отсчёта в другую (их конкретный вид в этом курсе лекций неважен); эти формулы релятивистские. Магнетизм невозможно описать без теории относительности. Магнетизм – релятивистский эффект.

^ 5.2. Сила Ампера

Сила Ампера, действующая на элемент тока , находящийся в магнитном поле , равна:

; (14.23)

. (14.23а)

Здесь α – угол между направлением тока и индукции поля . Сила Ампера перпендикулярна как проводнику с током, так и линиям индукции:

.

Направление силы Ампера можно найти по правилу буравчика в соответствии с определением (14.23) как векторного произведения, а можно воспользоваться опять школьным правилом левой руки (рис.14.20).

Если поле однородно, а отрезок провода – прямой, то из (14.22) получим закон Ампера в школьной формулировке:

; (14.23б)

. (14.23в)

Рассмотрим взаимодействие параллельных токов, находящихся на расстоянии d (рис.14.21). Проводники будем считать достаточно длинными. Пусть токи текут в одну и ту же сторону: от нас за плоскость чертежа. Ток I ₁ создаёт там, где находится второй проводник, поле с индукцией (см.14.13):

,

направленной в плоскости чертежа вниз (правило буравчика). Тогда сила Ампера, действующая на элемент второго тока , равна

,

так как ток перпендикулярен полю ; причём направлена к первому проводнику (правило левой руки). Окончательно:

;

.

Сила, действующая на единицу длины второго провода, равна:

.

Аналогично можно получить силу, действующую на единицу длины первого провода со стороны магнитного поля второго тока:

.

Силы равны и противоположны: это третий закон Ньютона.

.

Токи, текущие в одинаковом направлении, притягиваются, а текущие в противоположных направлениях – отталкиваются.

^ 6.1. Рамка с током в однородном магнитном поле

Рассмотрим прямоугольную рамку в однородном магнитном поле. Две стороны рамки длиной а параллельны полю, две других длиной b находятся к нему под углом. Нормаль к рамке составляет угол α с линиями поля (рис.14.22).

Силы Ампера, действующие на стороны длиной b, уравновешивают друг друга – они направлены по одной прямой. Силы, действующие на стороны длиной а, составляют пару сил:

и по закону Ампера

.

Плечо пары сил (расстояние между линиями их действия) равно

,

Момент пары сил равен

.

Произведение – это площадь рамки, а – это магнитный момент рамки. Тогда

.

Направлен момент пары сил так же как и векторное произведение , то есть получаем формулу (14.1):

.

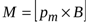Работа по повороту рамки с током в магнитном поле. Энергия рамки в магнитном поле

Н
айдём работу внешних сил по повороту рамки с током, имеющей магнитный момент 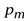, на угол против часовой стрелки (рис.14.22). Она равна

и идёт на увеличение энергии рамки в магнитном поле:

.

Тогда

.

Отсюда

,

, (14.24)

так как , а и не зависят от угла .

^ 6.2. Рамка с током в неоднородном магнитном поле

Поместим рамку с током или магнитную стрелку с магнитным моментом в не однородное магнитное поле (рис.14.23). Тогда силы 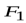и не будут параллельны и возникает равнодействующая, направленная вдоль поля. Если угол 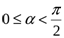, то равнодействующая направлена в сторону сильного поля: магнитный момент втягивается в область сильного поля.

И
наоборот (рис.14.24): если , то магнитный момент выталкивается из области сильного поля.

М
ожно вычислить результирующую силу, действующую на магнитный момент в магнитном поле. Из темы «Механика»:

;

тогда

.

Так что если 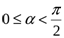, то . Если поле усиливается вдоль оси OX , то проекция результирующей силы на ось OX положительна:

.

Есл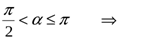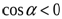и , и

.

^ 7. Эффект Холла (см.лаб.работу 2-15)

8. Поток вектора магнитной индукции

По определению потока любого векторного поля поток вектора магнитной индукции через элементарную площадку равен:

, (14.25)

где – угол между вектором и единичным вектором нормали к площадке 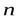(рис.14.25).

М агнитный поток через любую поверхность – это интеграл по поверхности:

.

Размерность магнитного потока – вебер:

.

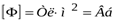Физический смысл магнитного потока: магнитный поток численно равен числу линий магнитной индукции, пронизывающих площадку.

Пример: найдём магнитный поток через сечение длинного соленоида. Поле однородно; нормаль к сечению совпадает по направлению с полем, тогда

.

Полное потокосцепление (суммарный поток через все N витков соленоида):

. (14.26)

^ 9. Теорема Остроградского-Гаусса для магнитного поля

Магнитный поток через произвольную замкнутую поверхность равен нулю:

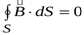. (14.27)

Физический смысл этой теоремы: магнитных зарядов нет. Для сравнения вспомним теорему Гаусса для электростатического поля: поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченных поверхностью:

.

Е сли отдельные тела можно зарядить либо только положительно, либо только отрицательно, поскольку существуют элементарные заряженные частицы – носители электрических зарядов двух разных видов, – то отделить один из магнитных полюсов от противоположного невозможно. Если разрезать на две части магнит, то каждая часть будет снова вести себя как самостоятельный магнит, имеющий на своих концах противоположные полюсы (рис. 14.26).

Что произойдет, если при делении дойти до того, что разбить магнит на отдельные атомы? Можно ли тогда отделить северный полюс от южного? Нет, даже отдельные атомы ведут себя как микроскопические, но тем не менее «полноценные» магниты с северным и южным полюсами. Оказывается, что даже отдельные элементарные частицы (например, электроны) представляют собой микромагниты. В настоящее время отсутствуют какие-либо экспериментальные доказательства того, что в природе могут существовать отдельные магнитные заряды (монополи), подобные электрическим. В отличие от электрических зарядов свободных магнитных “зарядов” в природе не существует. Нет их и в полюсах постоянных магнитов. Поэтому линии магнитной индукции не могут обрываться на полюсах.

^ 10. Работа по перемещению проводника с током в магнитном поле

Пусть проводник с током I длиной l, перпендикулярный индукции магнитного поля , перемещается в магнитном поле перпендикулярно полю под действием силы Ампера (рис.14.27). Тогда работа силы Ампера при перемещении на dh равна:

.

. (14.28)

Если сила тока не меняется, то

. (14.28а)

Р
абота по перемещению проводника с током в магнитном поле равна произведению силы тока на изменение магнитного потока (на пересечённый проводником магнитный поток). Площадка – это заметённая проводником в процессе движения площадь.

Этот вывод универсален: работа по изменению магнитного потока через замкнутый контур вычисляется так же, независимо от того, за счёт чего изменяется магнитный поток: или контур деформировали, или изменяли его ориентацию в пространстве или даже если меняли индукцию поля. В последнем случае это – работа по поддержанию тока постоянным при изменении магнитного потока через контур вследствие изменения самого поля .
Магнитное поле и его характеристики

Магнитное поле создаётся любыми токами или движущимися зарядами. Взаимодействие токов (движущихся зарядов) осуществляется посредством магнитного поля. Магнитное поле проявляется в том, что на токи, помещённые в магнитное поле, действует сила. Магнитное поле также действует на магнитную стрелку (компаса), поворачивая её.

Величина магнитного поля характеризуется магнитной индукцией . Это – силовая характеристика поля. Механический вращающий момент силы пропорционален величине :

, (14.1)

где α – угол между вектором магнитной индукции и магнитным моментом магнитной стрелки или витка с током (14.2). То же самое можно записать в виде векторного произведения:

. (14.1а)

Замкнутый виток с током I имеет магнитный момент , направленный перпендикулярно плоскости витка по правилу буравчика (правого винта), если вращать буравчик по направлению тока (рис.14.1):

. (14.2)

Здесь – площадь витка, – единичный вектор нормали к витку (); его направление связано с направлением тока также правилом буравчика.Если вплотную друг к другу намотано N витков, то магнитный момент такой катушки:

. (14.2а)

Величина магнитного момента равна соответственно

(14.2)

или

.

По определению, величина магнитной индукции в данной точке поля численно равна максимальному вращающему моменту силы, действующему на виток (или магнитную стрелку) с единичным магнитным моментом:

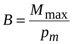. (14.3)

В самом деле, из (14.1) следует, что вращающий момент максимален при и .

Размерности:

;

Замечание: определение магнитной индукции через вращающий момент (14.3) или (14.1) – не единственно возможное; можно также ввести определение через силу Ампера (см. дальше); – это не принципиально: оба определения эквивалентны.

Индукция магнитного поля – векторная силовая характеристика; можно изобразить графически. Например, на рис.14.2 изображено однородное поле. Вектор вращающего момента силы на направлен перпендикулярно обоим векторам ( и ) из-за рисунка 14.2, а к нам в соответствии с правилами для векторного произведения (14.1а). Если виток с током свободен и может вращаться, то он развернётся так, что его магнитный момент сориентируется по полю; тогда , , и момент сил тоже обратится в ноль: . Это – состояние равновесия (рис.14.2, б). То же самое для магнитной стрелки (рис.14.3): она развернётся по полю северным концом (обозначение северного конца – N, южного – S) в направлении линий магнитной и
ндукции (рис.14.3).

Ещё одна характеристика магнитного поля – это напряжённость поля .

В веществе индукция магнитного поля отличается от индукции в вакууме . Это можно объяснить так: при помещении вещества (магнетика) во внешнее поле в веществе под действием поля возникают микротоки (термин Ампера – «молекулярные токи» не совсем правилен). Микротоки вещества сами создают дополнительную индукцию, так что индукция поля в веществе описывает суммарное поле: внешнее поле токов проводимости и микротоков вещества.

Напряжённость поля описывает только поле макротоков (токов проводимости). Напряжённость поля одинакова в вакууме и в веществе.

Можно провести аналогию с характеристиками электростатического поля – напряжённостью и вектором электрического смещения :

аналогично , так как описывает суммарное поле свободных и связанных зарядов;

аналогично , так как описывает только поле свободных зарядов и одинаково в вакууме и в веществе.

Связь между характеристиками поля такая:

, (14.4)

и аналогична соответствующей формуле для электростатического поля:

.

Константа в (14.4) называется магнитной постоянной.

– магнитная проницаемость вещества. Она показывает, во сколько раз индукция магнитного поля в веществе больше, чем в вакууме :

. (14.5)

Магнитная проницаемость – безразмерная величина:

.
2. Закон Био-Савара-Лапласа. Принцип суперпозиции

Одна из задач электродинамики – вычисление полей, созданных зарядами и токами. В частности, нужно научиться определять в произвольной точке пространства индукцию магнитного поля, созданного каким-либо электрическим током.

Для магнитного поля, как и для электростатического, справедлив принцип суперпозиции: индукция поля, созданного в данной точке несколькими токами, равна векторной сумме индукций полей, созданных в данной точке каждым током в отдельности:

. (14.6)

В случае непрерывного проводника принцип суперпозиции выглядит так:

. (14.7)

Здесь интеграл берётся по всему проводнику. Индукция, созданная непрерывным проводником с током, равна интегралу от элементарных индукций полей, созданных каждым элементом тока в отдельности. Элемент тока – это произведение силы I тока на элемент длины провода .

Рассмотрим произвольный проводник с током (рис.14.4). Рассчитать элементарную индукцию , созданную элементом тока , позволяет закон Био-Савара-Лапласа (14.8):

; (14.8)

. (14.8а)

Здесь – элемент тока, создающий поле в точке А;

– радиус-вектор точки А; он проводится от элемента тока к точке;

– угол между радиус-вектором и элементом тока.

В соответствии с (14.8), вектор направлен по правилу буравчика: по касательной к окружности, проходящей через точку А и перпендикулярной вектору , с центром на продолжении вектора .

На рис.14.4 вектор направлен из-за чертежа к нам, перпендикулярно обоим векторам – и .
3. Применение закона Био-Савара-Лапласа для расчёта индукции магнитного поля