Изотопные (эквивалентные) узлы

Два узла называются изотопными если от одного к другому можно перейти последовательно выполняя преобразования называться элементарными изотопами.

Элементарные изотопии.

1. Замена одного из звеньев узла двумя новыми отрезками, которые вместе с ним образуют контур треугольника, пересекающегося с прежним узлом только по заменному звену.

2. Замен 2х соседних звеньев одним отрезком, который вместе с ним образует контур треугольника, пересекающихся с прежним узлом только по замененным звеньям.

27.Проблема распутывания узлов: алгоритм Рейдемейстера.

Проблема распутывания узлов.

Найти алгоритм, который по любой диаграмме узла узнает, тривиален узел или нет. (Проблема распутывания – это это проблема сравнения с тривиальным узлом.)

Операции Рейдемейстера

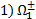- раскручивание (и закручивание) петелек;

2) - соскальзывание одной ветви с другой и налезание одной ветви на другую;

3) 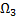- переброс ветви через двойную точку.

Операции, помеченные плюсом, уменьшают число двойных точек (а значит, упрощают диаграмму узла); операции, помеченные минусом увеличивают это число. Операция 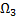не меняет число двойных точек.

Теорема. Два узла эквивалентны тогда и только тогда, когда от диаграммы одного узла к диаграмме другого можно перейти с помощью конечного числа операций .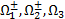

Теорема Рейдемейстера сводит трудную пространственную задачу эквивалентности двух узлов к более простой «плоской» задаче о превращении одной диаграммы узла в другую с помощью трех известных операций .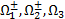

Этот алгоритм не всегда умеет распутать тривиальные узлы.