Вопрос. Полином Конвея

Наряду с обычными зацеплениями можно рассматривать ориентированные зацепления, то есть зацепления, на каждой компоненте которых задана ориентация – направление обхода. Для них точно так же определяются плоские диаграммы (с добавлением стрелочек, указывающих ориентацию компонент), а также движения Рейдемейстера (с согласованными ориентациями до и после движения).

Перейдем теперь к построению инвариантов ориентированных зацеплений. Рассмотрим три диаграммы ориентированных зацеплений, которые совпадают в некоторой малой окружности, а внутри нее отличаются так, как показано на рис. 4 сверху. Обозначим такие тройки диаграмм через L , L , L 0.

 

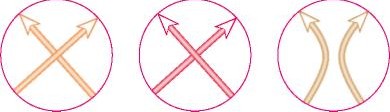
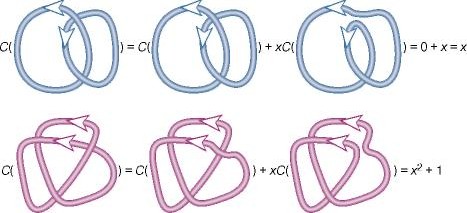
Рис. 4 Вычисление полинома Конвея

Можно показать, что существует единственный инвариант узла C со значениями в полиномах от одной переменной x, равный единице на тривиальном узле, нулю на тривиальном зацеплении из двух или более компоненты для каждой тройки диаграмм соотношению L , L , L 0удовлетворяющий C (L )− C (L ) = C (L 0), называемому соотношением типа Конвея. Такой инвариант называется полиномом Конвея.

Полином Конвея удобен для вычисления. Пусть дана диаграмма L зацепления с n перекрестками. Тогда, изменяя типы некоторых перекрестков (с прохода на переход и наоборот), можно превратить эту диаграмму в тривиальную. Это делается так. Рассмотрим проекцию одной из компонент зацепления и будем прокладывать веревку вдоль нее начиная с некоторой точки. В каждой вершине будем располагать второй виток веревки выше первого (то есть будем класть веревку каждый раз поверх себя). В итоге получим узел, который, очевидно, будет тривиальным. Далее расположим различные компоненты зацепления одна под другой. Получим диаграмму тривиального зацепления. Теперь у нас есть точный алгоритм вычисления полинома Конвея: мы выбираем диаграмму L ' тривиального зацепления, получаемую из диаграммы L заменой некоторых типов перекрестков. Далее мы поочередно изменяем тип перекрестка в каждом из них и записываем соответствующее соотношение типа Конвея (в котором начальная и измененная диаграммы играют роль L ₊, L _-, а роль диаграммы L 0играет диаграмма с n −1перекрестком). В итоге мы получаем, что значение полинома Конвея C (L) равно значению полинома C (L '), то есть нулю или единице в зависимости от числа компонент, плюс сумма значений (со знаками плюс или минус) полинома Конвея на диаграммах с n −1 перекрестком.Таким образом, мы свели вычисление значения полинома Конвея на диаграмме с n перекрестками к вычислению на диаграммах с n −1 перекрестком. Продолжая в этом направлении, мы сведем это вычисление к диаграммам с 0 перекрестков, которые являются тривиальными узлами или зацеплениями.

Проиллюстрируем приведенный алгоритм на зацеплении Хопфа, а затем на правом трилистнике (см.рис. 4 внизу).

К сожалению, на левом трилистнике значение полинома Конвея такжеравно 1 õ 2, то трилистник. Между тем существует много других инвариантов I (гораздо более мощных, чем полином Конвея), равных единице на тривиальном узле и основанных на соотношениях (также называемых соотношениями типа Конвея) вида aI (L ₊) + bI (L _-) = cI (L 0), где a, b, c – некоторые функции от одной или двух переменных. В случае полинома Конвея a = 1, b = −1, c = x. В частности, такие инварианты позволяют отличить левый трилистник от правого. Приведем список наиболее известных из этих инвариантов:

полином Джонса от одной переменной

 

 

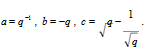
полином HOMFLY от двух переменных a = x, b = − t, c = 1. Наиболее сильный из этих инвариантов – полином Джонса от двух переменных λ, q, в котором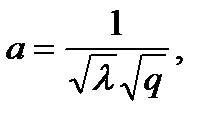

 

 

 

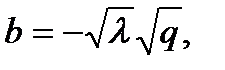
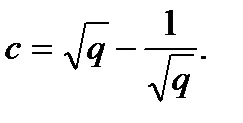
34. Примеры вычисления полинома Конвея.

 

 

ИЛИ:

 

 

Вопрос 35. Теория кос

Теория кос – это реальная и живая наука, возникшая в 20-ых годах прошлого века тогда еще молодым немецким алгебраистом Э. Артином по заказу ткацкой фабрики: он выполнял, как бы сказали сегодня, хоздоговорную работу для этого предприятия.

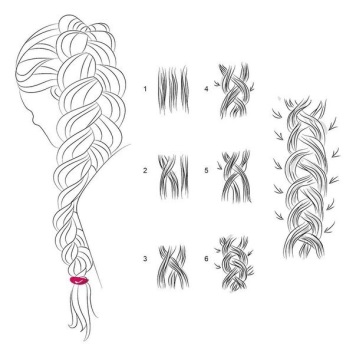
Приведем примеры кос (рис. 1).

К1	К2	К3	К4
«Девичья коса»	Тривиальная коса	Крашеная коса	Циклическая коса
Диаграммы – проекция косы на плоскость
Рис. 1. Примеры кос из трех и четырех нитей

Косу можно себе представлять так: в верхний и нижний край вертикальной доски вбито по n гвоздиков (n может равняться 1, 2, 3, …) – каждый из гвоздиков верхнего основания соединен нитью с одним из гвоздиков нижнего; нити попарно не пересекаются и все время должны опускаться вниз (нить не имеет права, повернувшись, начать подниматься вверх: фигуры на рисунке 2, например, косами не являются).

 

 

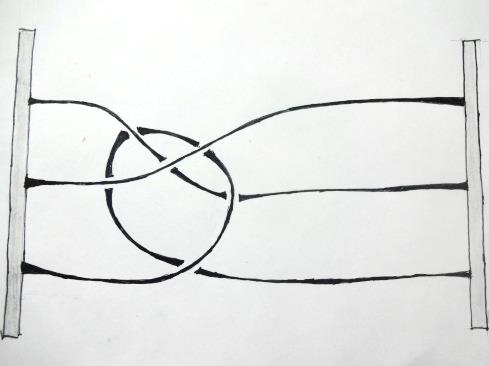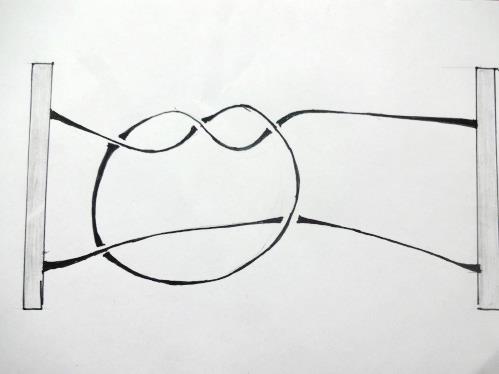Рис. 2. Эти фигуры не являются косами: их нити имеют восходящий характер

Две косы считаются эквивалентными (т. е. одинаковыми), если одну можно превратить в точную копию другой, двигая нити (без разрывов и склеиваний) так, чтобы каждая точка каждой нити перемещалась только в горизонтальной плоскости. Такое движение показано на рисунке 3.

Рис. 3. Геометрическое доказательство тривиальности косы

Коса К тривиальна, ибо она легко превращается (см. рис. 3) в косу из четырех вертикальных нитей).

На рисунке 1 вверху у начала каждой нити указан ее порядковый номер. Внизу снова указан номер каждой нити – но здесь номера не обязаны идти по порядку: каждой косе соответствует перестановка номеров ее нитей. Так, косами К₁, К₃, К₄ на рисунке 1 отвечают перестановки:

, , .
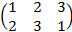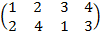Среди кос на рисунке 1 выделяется крашеная коса К₃: так она называется вовсе не потому, что нарисовали ее нити разными цветами: крашеной называется любая коса, которой отвечает тождественная перестановка , т. е. коса, сохраняющая порядок номеров нитей.

Тривиальная коса, все нити которой вертикальные прямые является частным случаем крашеной косы.

Среди кос следует выделить, кроме крашеных, в известном смысле противоположные им - циклические косы: это косы, переставляющие все номера нитей по единому циклу, как это делает коса К₄: 1®2® 4 ®3 ®1.

 

2. Алгебра кос

Косы - один из простейших геометрических объектов, легко поддающийся «алгебраизации»: косы с одинаковым числом нитей можно умножать. Делается это совсем просто (см. рис. 4): нужно приложить одну косу к другой, склеив соответствующие нити, и удалить ставшие ненужными гвоздики (нижние гвозди первой косы верхние – второй).

К	L	M = K × L
Рис. 4. Умножение кос

Такое умножение обладает рядом свойств обычного умножения чисел: выполняется ассоциативный закон

К₁(К₂К₃)=(К₁К₂)К_3,

есть аналог единицы – тривиальная коса К₂ = 1, для которой

.

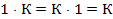Умножение кос не коммутативно.
Есть и аналог деления: у каждой косы К имеется обратная коса 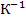: для нее

.

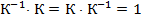Рассмотрим данную операцию на рисунке 5.

К	К-1	К × К-1 = 1

 

Проблему классификации кос можно решать с помощью

основных соотношений теории кос: