Задание 1. В партии из N=15 изделий n=4 имеют скрытый дефект. Какова вероятность того, что из взятых наугад m=3 изделий k=2 изделий являются дефектными?
Решение.
Пусть событие А – " из взятых наугад m=3 изделий k=2 изделий являются дефектными ".
Общее число исходов испытания равно числу способов, которыми можно выбрать 3 изделия из 15, т.е. числу сочетаний из 15 элементов по 3 (порядок в данном случае не имеет значения).
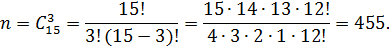
Определим число исходов, благоприятствующих событию А.
2 дефектных изделия из 4 можно выбрать 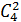 . способами; 3-е изделие – не дефектное – можно выбрать из 11 (15-4=11) не дефектных 11-ю
. способами; 3-е изделие – не дефектное – можно выбрать из 11 (15-4=11) не дефектных 11-ю  способами. По правилу произведения
способами. По правилу произведения
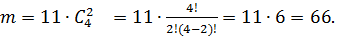
Искомая вероятность равна
Р(А) = 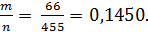
Ответ: Р(А)= 0,145.
Задание 2. В магазине выставлены для продажи n=12 изделий, среди которых k =4 изделий некачественные. Какова вероятность того, что взятые случайным образом m =3 изделий будут некачественными?
Решение.
Пусть событие А – " взятые случайным образом 3 изделия будут некачественными".
Вероятность взять 1-е некачественное изделие равна 4/12, 2-е – 3/11,
3-е – 2/10. Тогда вероятность искомого события равна:
Р(А)= 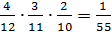 =0,0182.
=0,0182.
Ответ: Р(А)= 0,0182.
Задание 3. На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: n1 =10 с первого завода, n2=20 со второго, n3 =20 с третьего. Вероятность качественного изготовления изделий на первом заводе p1=0,9, на втором p2=0,8, на третьем p3=0,6. Какова вероятность того, что взятое случайным образом изделие будет качественным?
Решение.
Пусть событие А = { взятое случайным образом изделие будет качественным }.
Можно сделать следующие предположения:
Н 1 – изделие поступило с 1-го завода;
Н 2 -- изделие поступило с 2-го завода;
Н 3 -- изделие поступило с 3-го завода.
Вероятности гипотез равны:
Р(Н 1 )= 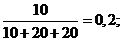
Р(Н 2 )= Р(Н 3 )= 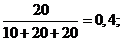
Условные вероятности равны
Р(А/Н1)=0,9; Р(А/Н2)= 0,8; Р(А/Н3)= 0,6.
По формуле полной вероятности имеем:
Р(А) = Р(Н1)* Р(А/Н1)+ Р(Н2)* Р(А/Н2)+ Р(Н3)* Р(А/Н3) = 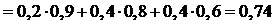 .
.
Ответ: Р(А)=0,74.
Задание 4. Дано распределение дискретной случайной величины Х. Найти математическое ожидание и среднее квадратическое отклонение.
| хi | -8 | -2 | ||
| pi | 0,1 | 0,3 | 0,4 | 0,2 |
Решение.
Найдем математическое ожидание М (Х):
M(X) = 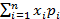 = -8*0,1 - 2*0,3 + 1*0,4 +3*0,2= -0,4.
= -8*0,1 - 2*0,3 + 1*0,4 +3*0,2= -0,4.
Найдем математическое ожидание
M(X2) = 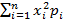 :
:
M(X2) = (-8)2*0,1+(- 2)2*0,3 + 12*0,4 +32*0,2= 9,8.
Дисперсия
D(X) = М (Х2)-(М(Х))2 = 9,8 – (-0,4)2 = 9,64.
Среднее квадратическое отклонение
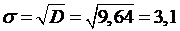 .
.
Ответ: M(X) =-0,4; 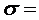 3,1.
3,1.
Задание 5. В городе имеются N =4 оптовых баз. Вероятность того, что требуемого сорта товар отсутствует на этих базах одинакова и равна p=0,1 Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.
Решение.
Пусть событие A – товар отсутствует на базе. Т.к. испытания независимы, воспользуемся формулой Бернулли:
Pn(k)= 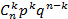
Здесь P (A) = p = 0.1; q= 1- p = 1- 0.1= 0.9; число испытаний n = 4; Возможные значения случайной величины: 0, 1, 2, 3,4.
Найдем соответствующие вероятности:
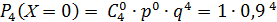 =0,6561.
=0,6561.
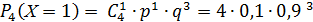 =0,2916.
=0,2916.
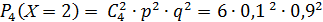 = 0,0486.
= 0,0486.
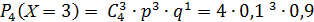 = 0,0036.
= 0,0036.
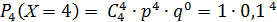 = 0,0001.
= 0,0001.
Контроль: 0,6561+0,2916+0,0486+0,0036+0,0001= 1,0.
Составим ряд распределения.
| Xi | |||||
| Pi | 0,6561 | 0,2916 | 0,0486 | 0,0036 | 0,0001 |
Задание 6. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно Mx =18, среднее квадратичное отклонение равно Ϭx =1. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале а=16, b=21.
Решение.
Найдем вероятность попадания в интервал по формуле
P (α < X < β) = Ф 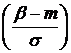 – Ф
– Ф 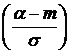 ,
,
где Φ(х)= 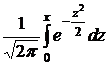 - функция Лапласа,
- функция Лапласа,
Φ(-х)= Φ(х).
По условию, mx =18; 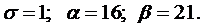
P (16 < X < 21) = Ф 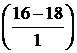 – Ф
– Ф 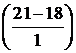 = Ф(-2) – Ф(3) = - Ф(2) +Ф(3) =
= Ф(-2) – Ф(3) = - Ф(2) +Ф(3) =
=-0,4772+0,49865= 0,02145.
Ответ: P (16 < X < 21) =0,02145.
Задание 7. Найти линейную среднюю квадратическую регрессию случайной величины Y на случайную величину X на основе заданного закона распределения двумерной случайной величины.
| X Y | |||
| 0,06 | 0,18 | 0,24 | |
| 0,12 | 0,13 | 0,27 |
Pешение.
Найдем законы распределения составляющих Х и Y
Сложив вероятности по столбцам, получим вероятности возможных значений X: P (2) = 0.06+0.12= 0.18; P (3) = 0.18+0.13 = 0.31; P (5) = =0.24+0.27=0.51.
Напишем закон распределения X:
| X | |||
| P | 0.18 | 0.31 | 0.51 |
Контроль: 0,18+0,31+0,51=1.
Сложив вероятности по строкам, аналогично получим закон распределения Y
| Y | ||
| P | 0.48 | 0.52 |
Контроль: 0,48+0,52=1.
3) Найдем числовые характеристики случайных величин X и Y.
Математическое ожидание M(X) = 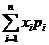 = 2∙0,18 +3∙0,31+5∙0,51=3,84.
= 2∙0,18 +3∙0,31+5∙0,51=3,84.
Дисперсия D(X) = М(X2)-(М(X))2
М(X2)= 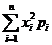 = 22 ∙0,18+32∙0,31+52∙0,52 = 16,26.
= 22 ∙0,18+32∙0,31+52∙0,52 = 16,26.
D(X) = 16.26 -(3,84)2 =1,5144.
Среднеквадратическое отклонение 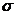 =
= 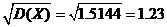 .
.
Аналогично находим
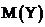 = 4∙0,48+6∙0,52=5,04.
= 4∙0,48+6∙0,52=5,04.
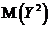 = 42∙0,48+62∙0,52= 26,4.
= 42∙0,48+62∙0,52= 26,4.
D(Y) = 26,4 -(5,04)2 =0,9984.
Среднеквадратическое отклонение
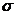 =
= 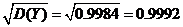 .
.
Найдем коэффициент корреляции r по формуле
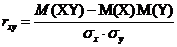 ,
,
Найдем 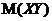 =
= 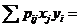 0,06∙2∙4+0,12∙2∙6+0,18∙3∙4+0,13∙3∙6+0,24∙5∙4+
0,06∙2∙4+0,12∙2∙6+0,18∙3∙4+0,13∙3∙6+0,24∙5∙4+
+0,26∙5∙6 = 0,48+1,44+2,16+2,34+4,8+7,8=19,02.
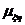 = 0,3-1,2∙0,2=0,3-0,24=0,06.
= 0,3-1,2∙0,2=0,3-0,24=0,06.
Коэффициент корреляции равен
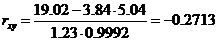 .
.
Коэффициент корреляции показывает, что связь между переменными слабая и обратная, т.е. у убывает с возрастанием х.
. Уравнения парной линейной регрессии имеет вид:

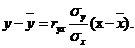
Подставим значения входящих в уравнение величин.
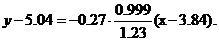
После упрощений получим уравнение регрессии
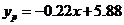 .
.
 2017-12-14
2017-12-14 18153
18153
