2017-12-14
21442
Задание 1. Рассчитать и построить гистограмму относительных частот по сгруппированным данным (смотри таблицу 1), где n i – частота попадания вариант в промежуток (xi,, xi + 1].
| i |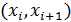 
| n i |
| 7 - 9 | ||
| 9 - 11 | ||
| 11 - 13 | ||
| 13 - 15 | ||
| 15 - 17 |
Решение.
Объем выборки n= 5+4+8+12+11=40.
Построим группированный статистический ряд относительных частот wi=mi/n
| i |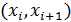
| wi |
| 7 - 9 | 0,125 | |
| 9 - 11 | 0,1 | |
| 11 - 13 | 0,2 | |
| 13 - 15 | 0,3 | |
| 15 - 17 | 0,275 |
Построим гистограмму относительных частот
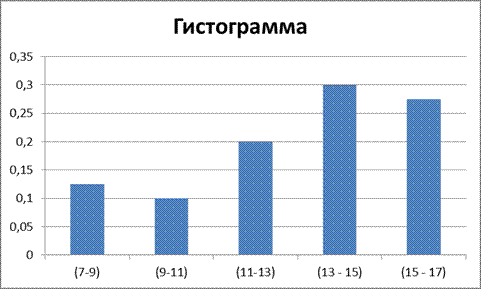
Задание 2. Найти несмещенную выборочную дисперсию на основании данного распределения выборки.
| xi | 0,01 | 0,04 | 0,08 | 0,14 |
| ni |
Решение.
Объем выборки n= 19+28+31+22=100.
Составим расчетную таблицу
| xi | 0,01 | 0,04 | 0,08 | 0,14 |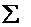 
|
| ni | |||||
| xi ni | 0,19 | 1,12 | 2,48 | 3,08 | 6,87 |
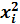 ∙ n i
| 0,0019 | 0,0448 | 0,1984 | 0,4312 | 0,6763 |
Вычислим выборочную среднюю по формуле:
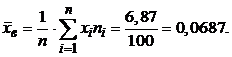
Выборочную дисперсиювычислим по формуле:
= 
.
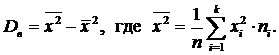
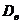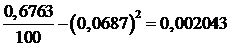Найдем исправленную выборочную дисперсию
.
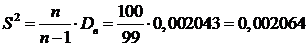Т.к. объем выборки большой, исправленная выборочная дисперсиянезначительно отличается от выборочной дисперсии.
Ответ: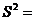 
0,002064.
Задание 3. Проверить нулевую гипотезу о том, что заданное значение а0 =58 является математическим ожиданием нормально распределенной случайной величины при 5% уровне значимости для двусторонней критической области, если в результате обработки выборки объема n = 10 получено выборочное среднее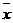 
=56, а выборочное среднее квадратичное отклонение равно s =4
Решение.
Сформулируем гипотезы.
Н0 : 
-- математическое ожидание нормально распределенной случайной величины равно а0 =58;
Н1: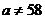 
-- математическое ожидание не равно 58.
Поскольку дисперсия генеральной совокупности неизвестна, для проверки основной гипотезы воспользуемся критерием Стьюдента:
,
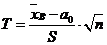где n = 10, а0 =58, 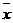=56, s =4.
Найдем наблюдаемое значение критерия
.
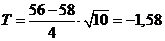Т.к. альтернативная гипотеза имеет вид: Н1 :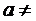 
58, то критическая область двухсторонняя.
По таблице критических точек распределения Стьюдента при заданном уровне значимости a = 0,05 и числу степеней свободы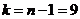 
находим Ткр (a,k)= Ткр (0,05;9)= 2,26. Т.к. 
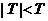кр, то нет оснований отвергнуть нулевую гипотезу, т.е. можно считать, что математическое ожидание нормально распределенной случайной величины равно а0 =58.
Ответ: Т=- 1,58; Ткр = 2,26, гипотеза Н0 принимается.
Задание 4. При уровне значимости α = 0,1 проверить гипотезу
H0: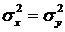 
о равенстве дисперсий двух нормально распределенных случайных величин X и Y на основе выборочных данных при альтернативной гипотезе H1: 
.
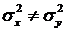| xi | ni | yi | mi |
Решение.
По данным выборкам найдем исправленные выборочные дисперсии:
для Х
| xi | ni | xi 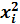∙ ni | ∙ ni
|
|
|
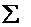Объем выборки n=15.
Вычислим выборочную среднюю по формуле:
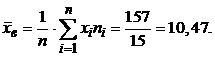
Выборочную дисперсиювычислим по формуле:
= 
.
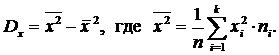
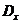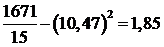Найдем исправленную выборочную дисперсию
.
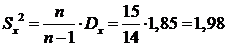для Y
| yi | mi | уi 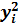mi |  ∙ mi
|
|
|
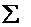Аналогично, найдем числовые характеристики для Y.
Объем выборки n=26.
Выборочная средняя:
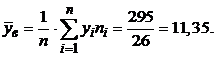
Выборочная дисперсия:
= 
.
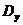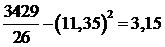Исправленная выборочная дисперсия:
.
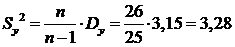Найдём наблюдаемое значение критерия Фишера
.
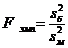где в числителе стоит большая дисперсия.
Т.к.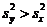 
, nх = 15, 
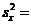1,98; nу = 26, 
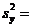3,28.
то наблюдаемое значение критерия равно
.
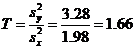k 1 = n1 – 1 = 26 – 1 = 25 и k 2 = n2 – 1 = 15 – 1 = 14 (числа степеней свободы).
С помощью встроенной функции EXCEL FPACПОБР при уровне значимости a = 0,1 и данным числам степеней свободы находим
Tкр (0.1; 25; 14) =.1,93. Т.к. Т < Ткр, то нет оснований отвергать нулевую гипотезу (т.е. можно считать, что дисперсии двух выборок равны).
Ответ: Т=1,66; Ткр = 1,93, гипотеза Н0 принимается.
Приложение 1
