Задание 1. Решить следующие задачи:
1.1. На предприятии брак составляет в среднем 3 % от общего выпуска изделий. Известно, что изделия высшего сорта составляют 85 % стандартной продукции.
Определить, какова вероятность того, что выбранное наугад изделие из произведенных на этом предприятии будет высшего сорта.
1.2. Из партии втулок, изготовленных за смену токарем, случайным образом отбирается для контроля 10 штук.
Какова вероятность того, что среди отобранных втулок 2 – второго сорта, если во всей партии 25 втулок первого сорта и 5 – второго?
1.3. Комиссия по качеству раз в месяц проверяет качество продуктов в двух из 30 магазинов, среди которых находятся и два известных вам магазина.
Выяснить, какова вероятность того, что в течение месяца они оба будут проверены.
1.4. Из 5 букв разрезной азбуки составлено слово “песня”. Ребенок, не умеющий читать, рассыпал буквы и затем собрал в произвольном порядке.
Какова вероятность того, что у него снова получилось слово “песня”?
1.5. Из 20 акционерных обществ 4 являются банкротами. Гражданин приобрел по одной акции шести акционерных обществ.
Какова вероятность того, что среди купленных акций две окажутся акциями банкротных акционерных обществ?
1.6. В группе спортсменов 7 лыжников и 3 конькобежца. Из нее случайным образом выделены 3 спортсмена.
Какова вероятность того, что все выбранные спортсмены окажутся лыжниками?
1.7. В партии 15 однотипных стиральных машин, 5 из которых изготовлены на заводе А, а 10 – на заводе В. Случайным образом отобрано 5 машин.
Какова вероятность того, что две из них изготовлены на заводе А?
1.8. На полке 6 радиоламп, из которых 2 неисправные. Случайным образом отбираются 2 радиолампы.
Выяснить, какова вероятность того, что отобранные радиолампы являются исправными.
1.9. На склад привезли 50 ящиков комплектующих изделий для одного из видов ЭВМ, но среди них оказалось 4 ящика комплектующих для другого вида ЭВМ. Наудачу взяли 6 ящиков.
Какова вероятность того, что в одном из этих 6 ящиков окажутся некомплектные детали?
1.10. Из стопки, в которой 8 книг и из них 2 – художественные, наугад связи 4 книги.
Какова вероятность того, что хотя бы одна из отобранных книг является художественной?
1.11. Магазин получил продукцию в ящиках с четырех оптовых складов: 4 ящика – с первого, 5 – со второго, 7 – с третьего и 4 ящика – с четвертого. Случайным образом выбран ящик для продажи.
Определить, какова вероятность того, что выбранный ящик будет с первого или с третьего склада.
1.12. В запасе ремонтной мастерской 10 поршневых колец, 3 из которых – восстановленные. Наудачу взяли 3 кольца.
Какова вероятность того, что среди взятых колец, 2 окажутся восстановленными?
1.13. В городе находятся 15 продовольственных и 5 непродовольственных магазинов. Случайным образом для приватизации были отобраны 3 магазина.
Какова вероятность того, что отобранные магазины окажутся непродовольственными?
1.14. В группе 8 спортсменов, из них 6 мастеров спорта.
Какова вероятность того, что из двух случайным образом отобранных спортсменов хотя бы один – мастер спорта?
1.15. В районе 100 поселков. В пяти из них находятся пункты проката сельхозтехники. Случайным образом отобраны 2 поселка.
Какова вероятность того, что в них окажутся пункты проката?
1.16. Из коробки, содержащей карточки с буквами “о”, “н”, “к”, “ь”, наугад вынимают одну карточку за другой и располагают в порядке извлечения.
Какова вероятность того, что в результате получится слово “конь”?
1.17. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из 3 человек.
Какова вероятность того, что в делегацию войдут две женщины и один мужчина, считая, что каждый из присутствующих с одинаковой вероятностью может быть избран в ее состав?
1.18. Из пруда, в котором плавают 40 щук, выловили 5 щук, пометили их и пустили обратно в пруд. Во второй раз выловили 9 щук.
Определить, какова вероятность того, что среди них окажутся только две помеченные щуки.
1.19. В бригаде четыре женщины и трое мужчин. Среди членов бригады разыгрываются 4 билета в театр.
Какова вероятность того, что среди обладателей билетов окажется две женщины и двое мужчин?
1.20. Из пяти карточек с буквами “а”, “б”, “в”, “г”, “д” наугад одну за другой выбирают две и располагают их в порядке извлечения.
Выяснить, какова вероятность того, что получится слово “да”.
1.21. Из 10 билетов выигрышными являются 2. Наудачу выбирают 5 билетов.
Какова вероятность того, что среди взятых билетов один окажется выигрышным?
1.22. В урне 3 белых и 7 черных шаров. Наугад извлекают 2 шара.
Какова вероятность того, что извлеченные шары окажутся черными?
1.23. Гражданин купил билет “Спортлото” и наугад отметил в нем 6 из имеющихся 49 номеров.
Какова вероятность того, что он правильно угадал 3 из 6 номеров, которые будут опубликованы в списке “выигрышных”?
1.24. В мастерскую для ремонта поступило 20 телевизоров. Известно, что 7 из них нуждаются в настройке. Мастер наугад выбирает 5 телевизоров.
Какова вероятность того, что из выбранных 2 телевизора нуждаются в настройке?
1.25. Производится подбрасывание двух игральных костей.
Какова вероятность того, что на обеих костях выпадет равное число очков?
1.26. Определить вероятность того, что случайно выбранное натуральное число от 1 до 30 включительно будет содержать цифру “1”.
1.27. В магазине из 100 пар зимних сапог одного фасона 10 коричневого цвета, а остальные – черного. Произвольно отбирают 8 пар сапог.
Какова вероятность того, что все выбранные сапоги окажутся черного цвета?
1.28. В магазине имеются 10 женских и 6 мужских шуб. Для анализа качества случайным образом отобрали 3 шубы.
Какова вероятность того, что среди отобранных шуб окажутся только мужские или только женские шубы?
1.29. В партии 20 радиоприемников, из них 5 являются неисправными. Наугад берут 3 радиоприемника.
Какова вероятность того, что в число выбранных войдут 1 неисправный и 2 исправных радиоприемника?
1.30. В коробке находится 6 одинаковых по форме и близких по диаметру сверл. Случайным образом сверла извлекаются из коробки.
Выяснить, какова вероятность того, что сверла извлекутся в порядке возрастания их диаметра.
Задание 2. Решить следующие задачи:
2.1. Имеются два ящика, содержащие типовые элементы замены (ТЭЗ). В первом ящике – 25 исправных и 5 неисправных, во втором – 27 исправных и 3 неисправных. Из каждого ящика наугад вынимают по одному ТЭЗ.
Найти вероятность того, что: а) оба ТЭЗ будут исправны; б) только один будет исправным; в) не более одного будет неисправным.
2.2. Два бомбардировщика преодолевают зону ПВО. Вероятность того, что будет сбит первый бомбардировщик, равна 0,7, второй – 0,8.
Найти вероятность: а) уничтожения одного бомбардировщика;
б) поражения двух бомбардировщиков; в) промахов.
2.3. В телестудии три телевизионные камеры. Вероятности того, что в данный момент камера включена, соответственно равны 0,8; 0,9; 0,7.
Определить, какова вероятность того, что в данный момент включены: а) две камеры; б) не более одной камеры; в) три камеры.
2.4. Инженер выполняет расчет, пользуясь тремя справочниками. Вероятности того, что интересующие его данные находятся в первом, втором, третьем справочнике, соответственно равны 0,6; 0,7; 0,8.
Определить, какова вероятность того, что интересующие инженера данные содержатся: а) только в одном справочнике; б) только в двух справочниках; в) во всех трех справочниках.
2.5. Стрелок произвел четыре выстрела по удаляющейся от него цели, причем вероятность попадания в цель в начале стрельбы равна 0,7, а после каждого выстрела уменьшается на 0,1.
Найти вероятность того, что цель будет поражена: а) четыре раза; б) три раза; в) не менее трех раз.
2.6. На заводе изготавливают железобетонные панели, из которых 90 % высшего сорта.
Найти вероятность того, что из трех наугад выбранных панелей высшего сорта будут: а) три панели; б) хотя бы одна панель; в) не более одной панели.
2.7. Вычислительный центр, который должен производить непрерывную обработку поступающей информации, располагает двумя вычислительными устройствами. Известно, что вероятность отказа за некоторое время t каждого из них равна 0,2.
Выяснить, какова вероятность безотказной работы за время t: а) каждого устройства; б) хотя бы одного устройства; в) одного устройства.
2.8. Самолет противника обнаруживается тремя радиолокаторами с вероятностями 0,8; 0,7; 0,5.
Найти вероятность обнаружения самолета: а) одним радиолокатором; б) двумя радиолокаторами; в) хотя бы одним радиолокатором.
2.9. В блок входят три радиолампы. Вероятности выхода из строя в течение гарантийного срока для них соответственно равны 0,3; 0,2; 0,4.
Найти вероятность того, что в течение гарантийного срока выйдут из строя: а) не менее двух радиоламп; б) ни одной радиолампы; в) хотя бы одна радиолампа.
2.10. Три автомата изготавливают детали. Вероятность того, что деталь, изготовленная первым автоматом, высшего качества, равна 0,9, второго – 0,7, третьего – 0,6. Наугад берут по одной детали с каждого автомата.
Определить, какова вероятность того, что из взятых деталей: а) все высшего качества; б) две высшего качества; в) хотя бы одна высшего качества.
2.11. Первый рабочий изготавливает 40 % изделий второго сорта, а второй – 30 %. У каждого рабочего наугад взято по 2 изделия.
Найти вероятность того, что: а) все 4 изделия второго сорта; б) хотя бы 3 изделия второго сорта; в) менее трех изделий второго сорта.
2.12. В первом ящике – 20 деталей, из которых 15 – стандартные. Во втором ящике – 30 деталей, из которых 25 – стандартные. Из каждого ящика наугад берут по одной детали.
Найти вероятность того, что: а) обе детали будут стандартными;
б) хотя бы одна деталь стандартная; в) обе детали нестандартные.
2.13. На двух станках обрабатываются однотипные детали. Появление бракованной детали для первого станка составляет 1 %, для второго станка – 4 %. С каждого станка взяли по одной детали.
Определить, какова вероятность того, что: а) обе детали стандартные; б) одна деталь стандартная; в) обе детали нестандартные.
2.14. Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй – 0,7, третий – 0,6.
Найти вероятность того, что студент сдаст: а) два экзамена;
б) не менее двух экзаменов; в) не более двух экзаменов.
2.15. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,7. Оба стрелка сделали по одному выстрелу.
Какова вероятность того, что цель поражена: а) хотя бы один раз; б) два раза; в) один раз?
2.16. Для аварийной сигнализации установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,9, второй – 0,7.
Найти вероятность того, что при аварии: а) сработают оба сигнализатора; б) не сработает ни один сигнализатор; в) сработает хотя бы один сигнализатор.
2.17. Из двух зенитных орудий сделано по одному выстрелу. При некоторых определенных условиях вероятность сбить самолет противника из первого зенитного орудия равна 0,4, из второго – 0,5.
Какова вероятность того, что: а) самолет уничтожен двумя снарядами; б) самолет поражен хотя бы одним снарядом; в) ни один снаряд не попал в цель?
2.18. При одном цикле обзора трех радиолокационных станций, следящих за космическим кораблем, вероятности его обнаружения соответственно равны 0,7; 0,8; 0,9.
Найти вероятность того, что при одном цикле обзора корабль будет обнаружен: а) тремя станциями; б) не менее чем двумя станциями; в) ни одной станцией.
2.19. Из всех деталей, находящихся в ящике 50 % изготовленны на заводе № 1, 20 % – на заводе № 2, 30 % – на заводе № 3. Наугад взято 3 детали.
Найти вероятность того, что: а) все детали с завода № 1; б) 2 детали с завода № 1; в) все 3 детали с разных заводов.
2.20. На участке кросса для мотоциклиста-гонщика имеется три препятствия. Вероятность успешного прохождения первого препятствия равна 0,4, второго – 0,5, третьего – 0,6.
Найти вероятность успешного преодоления: а) трех препятствий; б) не менее двух препятствий; в) двух препятствий.
2.21. Вычислительная машина состоит из четырех блоков. Вероятность безотказной работы в течение времени t первого блока равна 0,4, второго – 0,5, третьего – 0,6, четвертого – 0,4.
Определить, какова вероятность того, что в течение времени t будут работать: а) все 4 блока; б) 3 блока; в) не менее трех блоков.
2.22. Независимо друг от друга работают 3 станка. Вероятность того, что первый станок в течение смены выйдет из строя, равна 0,1, второй – 0,2 третий – 0,2.
Найти вероятность того, что в течение смены выйдут из строя:
а) не менее двух станков; б) 2 станка; в) 3 станка.
2.23. Вероятность выигрыша по лотерейному билету первого выпуска равна 0,2, второго – 0,3. Имеется по 2 билета каждого выпуска.
Какова вероятность того, что выигрышными окажутся: а) 3 билета; б) не менее трех билетов; в) менее трех билетов?
2.24. Трое рабочих собирают подшипники. Вероятность того, что подшипник, собранный первым рабочим, будет высшего качества, равна 0,7, вторым – 0,8, третьим – 0,6. Для контроля взято по одному подшипнику из собранных каждым рабочим.
Какова вероятность того, что высшего качества будут: а) все подшипники; б) 2 подшипника; в) хотя бы один подшипник?
2.25. В первой коробке находится 20 деталей, из которых 13 являются стандартными; во второй – 30, из которых 26 стандартные. Из каждой коробки наугад берут по одной детали.
Найти вероятность того, что: а) обе детали окажутся нестандартными; б) одна деталь нестандартная; в) обе детали стандартные.
2.26. В цехе имеется три резервных электродвигателя. Для каждого из них вероятность того, что в данный момент он включен, соответственно равна 0,2; 0,3; 0,1.
Определить, какова вероятность того, что включены: а) 2 электродвигателя; б) хотя бы один электродвигатель; в) 3 электродвигателя.
2.27. На сборку поступают детали с трех станков. Первый станок дает 20 % однотипных деталей, второй – 30, третий – 50 % деталей, поступающих на сборку.
Найти вероятность того, что из трех наугад взятых деталей: а) три с разных станков; б) три с третьего станка; в) две с третьего станка.
2.28. Вероятность поражения цели первым стрелком при одном выстреле равна 0,7, вторым – 0,5. Оба стрелка сделали по одному выстрелу.
Выяснить, какова вероятность того, что цель будет поражена: а) двумя стрелками; б) хотя бы одним стрелком; в) только одним стрелком.
2.29. Первый станок-автомат выпускает 1 % брака, второй – 1,5, третий – 2 %. Случайным образом отобрали по одной детали с каждого станка.
Найти вероятность того, что стандартными окажутся: а) три детали; б) две детали; в) хотя бы одна деталь.
2.30. Три команды спортивного общества А состязаются соответственно с тремя командами общества В. Вероятности выигрыша первой, второй и третьей команд из общества А у соответствующих команд из общества В равны 0,7; 0,6; 0,4. Команды провели по одной встрече.
Какова вероятность того, что команды общества А выигрывают:
а) две встречи; б) хотя бы две встречи; в) три встречи?
Задание 3. Решить следующие задачи:
3.1. Три оператора радиолокационной установки производят соответственно 25, 35 и 40 % всех измерений, допуская при этом 5, 4 и
2 % ошибок.
1. Определить вероятность проведения ошибочного измерения для установки в целом?
2. Найти вероятность того, что ошибочное случайно проведенное измерение принадлежит третьему оператору.
3.2. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; 7 – с вероятностью 0,7; 4 – с вероятностью 0,6 и 2 стрелка – с вероятностью 0,5. Наудачу выбранный стрелок производит выстрел по мишени.
1. Найти вероятность того, что произойдет попадание.
2. Если известно, что стрелок попал в мишень, то следует найти вероятность того, что он принадлежит к первой группе стрелков, попадающих с вероятностью 0,8.
3.3. Для участия в студенческих спортивных соревнованиях выделено из первой группы 5 студентов, из второй и третьей – соответственно 6 и 10 студентов. Вероятность выполнить норму мастера спорта для студентов первой группы равна 0,3, второй – 0,4, третьей – 0,2.
Найти вероятность того, что: а) наугад выбранный студент выполнит норму матера спорта; б) студент, выполнивший норму мастера спорта, учится во второй группе.
3.4. На сортировочную станцию прибывают полувагоны, платформы и крытые вагоны с вероятностями 0,25, 0,3 и 0,45 соответственно. Вероятность неисправности полувагона равна 0,02; платформы – 0,015; крытого вагона – 0,01.
1. Найти вероятность того, что поступивший на осмотр вагон окажется неисправным.
2. Если поступивший на осмотр вагон оказался неисправным, то следует найти вероятность того, что этот вагон является платформой.
3.5. Электролампы изготавливаются на двух заводах. Первый завод производит 60 % от общего количества электроламп, второй –
40 %. Известно, что 70 % продукции первого завода и 80 % второго являются изделиями высшего качества. В магазин поступает продукция обоих заводов.
1. Какова вероятность того, что купленная в магазине лампа окажется высшего сорта?
2. Если купленная лампа оказалась высшего сорта, то следует определить, какова вероятность того, что она изготовлена на первом заводе.
3.6. В двух коробках имеются однотипные конденсаторы. В первой коробке находится 20 конденсаторов, из которых 2 – неисправных, во второй – 10, из которых 3 – неисправных.
1. Найти вероятность того, что наугад взятый конденсатор из случайно выбранной коробки годен к использованию.
2. Если наугад взятый конденсатор оказался годным, то необходимо определить, из какой коробки он вероятнее всего взят.
3.7. Самолет может выполнять задания на больших, средних и малых высотах, причем на больших высотах предполагается совершить 25 % всех полетов, на средних – 10 и на малых – 65 %. Вероятности выхода самолета на заданный объект на больших, средних и малых высотах соответственно равны 0,75; 0,9; 0,95.
1. Найти вероятность выхода самолета на заданный объект.
2. При условии выхода самолета на заданный объект определить, какова вероятность того, что полет происходил на малой высоте.
3.8. Прибор может работать в трех режимах: нормальном, форсированном и недогруженном. Нормальный режим наблюдается в 50 % случаях работы прибора, форсированный – в 30, недогруженный –
в 20 %. Надежность прибора (вероятность безотказной работы в течение заданного времени t) для нормального режима равна 0,8, для форсированного – 0,5, для недогруженного – 0,9.
1. Найти полную надежность прибора.
2. Если прибор проработал безотказно в течение времени t, то следует найти вероятность того, что он работал в форсированном режиме.
3.9. В пяти ящиках с 30 шарами в каждом содержится по 5 красных шаров, в шести других ящиках с 20 шарами в каждом – по 4 красных шара.
Найти вероятность того, что: а) из наугад взятого ящика наугад взятый шар будет красным; б) наугад взятый красный шар содержится в одном из первых пяти ящиков.
3.10. На предприятии изготовляются изделия определенного вида на трех поточных линиях. На первой линии производится 20 % изделий от всего объема их производства, на второй – 30, на третьей –
50 %. Процент годности изделий для каждой из линий равен 95, 98 и 97 соответственно.
1. Найти вероятность того, что наугад взятое изделие, выпущенное предприятием, окажется бракованным.
2. Если выбранное наугад изделие оказалось бракованным, то следует определить на какой линии оно скорее всего изготовлено.
3.11. В канцелярии работают 4 секретаря, которые обрабатывают соответственно по 40, 10, 30 и 20 % исходящих документов за одно и то же время. Вероятности неверной адресации документов секретарями равны 0,01, 0,04, 0,06, 0,02 соответственно.
1. Найти вероятность того, что наугад выбранный исходящий из канцелярии документ будет неверно адресован.
2. Найти вероятность того, что документ, оказавшийся неверно адресованным, отправлен третьим секретарем.
3.12. В дисплейном классе имеется 10 персональных компьютеров первого типа и 15 – второго типа. Вероятность того, что за время работы на компьютере первого типа не произойдет сбоя, равна 0,9, а на компьютере второго типа – 0,7.
Какова вероятность того, что: а) на случайно выбранном компьютере за время работы не произошло сбоя; б) компьютер, во время работы на котором не произошел сбой, первого типа?
3.13. Сообщение может передаваться по одному из десяти каналов связи, 2 из которых находятся в отличном состоянии, 5 – в хорошем и 3 – в посредственном. Вероятности правильной передачи сообщения для каналов указанных видов равны 0,95, 0,9, 0,7 соответственно. По выбранному наугад каналу передано сообщение.
1. Найти вероятность того, что оно будет передано без искажений.
2. Если посланное сообщение передано без искажений, то следует найти вероятность того, что оно посылалось по каналам, находящимся в хорошем состоянии.
3.14. В телевизионном ателье имеется 2 кинескопа первого типа и 8 кинескопов второго типа. Вероятности выдержать гарантийный срок для кинескопов первого и второго типов равны 0,9 и 0,6 соответственно.
1. Найти вероятность того, что выбранный наугад кинескоп выдержит гарантийный срок.
2. Если выбранный наугад кинескоп выдержал гарантийный срок, то необходимо найти вероятность того, что это был кинескоп первого типа.
3.15. На двух станках обрабатываются однотипные детали. Вероятность брака для первого станка составляет 0,03, для второго – 0,02. Обработанные детали складываются в одном месте, причем деталей, обработанных на первом станке, вдвое больше, чем на втором станке.
Выяснить, какова вероятность того, что: а) взятая наугад деталь будет стандартной; б) наугад взятая стандартная деталь изготовлена на первом станке.
3.16. Детали попадают на обработку на один из трех станков с вероятностями, соответственно равными 0,2; 0,3 и 0,5. Вероятность получения бракованной продукции при обработке на первом станке равна 0,02, на втором – 0,03, на третьем – 0,01.
1. Найти вероятность того, что случайно выбранная после обработки деталь окажется стандартной.
2. Если случайно выбранная деталь оказалась стандартной, то нужно определить, какова вероятность того, что она обрабатывалась на втором станке.
3.17. Для поиска спускаемого аппарата космического корабля выделено 4 вертолета первого типа и 6 – второго. Каждый вертолет первого типа обнаруживает находящийся в районе поиска аппарат с вероятностью 0,6, вертолет второго типа – с вероятностью 0,7.
1. Найти вероятность того, что выбранный наугад вертолет обнаружит аппарат.
2. Если вертолет обнаружил спускаемый аппарат, то необходимо найти вероятность того, что это был вертолет второго типа.
3.18. Комплектовщик получает для сборки 30 % деталей с завода № 1, 20 % – с завода № 2, остальные – с завода № 3. Вероятность того, что деталь с завода № 1 – высшего качества, равна 0,9, с завода
№ 2 – 0,8, с завода № 3 – 0,6.
Найти вероятность того, что: а) случайно взятая деталь окажется высшего качества; б) наугад взятая деталь высшего качества изготовлена на заводе № 2.
3.19. По линии связи могут передаваться сигналы типа А и В с вероятностями 0,8 и 0,2 соответственно. В среднем, принимается 60 % сигналов типа А и 70 % – типа В. По линии связи передается один сигнал.
1. Какова вероятность того, что этот сигнал будет принят?
2. Если переданный сигнал принят, то следует найти вероятность того, что это был сигнал типа А.
3.20. Радиолокационная станция ведет наблюдения за объектом, который может применять или не применять помехи. Если объект не применяет помехи, то он обнаруживается радиолокационной станцией с вероятностью 0,8, если применяет – то с вероятностью 0,4. Известно, что объект применяет помехи в 70 % случаев работы.
1. Найти вероятность обнаружения объекта радиолокационной станцией.
2. Если объект обнаружен радиолокационной станцией, то следует найти вероятность того, что это произошло при применении объектом помех.
3.21. Три автомата изготавливают однотипные детали, которые поступают на общий конвейер. Производительность первого, второго и третьего автоматов соотносятся как 2:3:5. Вероятность того, что деталь с первого автомата высшего качества, равна 0,8, со второго – 0,6, с третьего – 0,7.
Найти вероятность того, что: а) наугад взятая деталь окажется высшего качества; б) взятая наугад деталь высшего качества изготовлена первым автоматом.
3.22. В состав блока входят 6 радиоламп первого типа и 10 – второго. Гарантийный срок обычно выдерживают 80 % радиоламп первого типа и 90 % – второго.
1. Определить, какова вероятность того, что выбранная наугад в составе блока радиолампа выдержит гарантийный срок.
2. Найти вероятность того, что радиолампа, выдержавшая гарантийный срок, первого типа.
3.23. Из высококачественных деталей собирается 40 % приборов, остальные – из деталей обычного качества. В первом случае надежность прибора (вероятность безотказной работы за время t) равна 0,9. Если прибор собран из обычных деталей, то его надежность равна 0,6.
1. Определить, какова надежность наугад выбранного прибора.
2. Если прибор в течение времени t работал безотказно, то следует найти вероятность того, что он собран из высококачественных деталей.
3.24. Из общего количества поступивших на сборку деталей 30 % привезены с завода № 1, остальные – с завода № 2. Вероятность брака для завода № 1 равна 0,02, для завода № 2 – 0,03.
Найти: а) вероятность того, что наугад взятая деталь окажется стандартной; б) вероятность изготовления наугад взятой детали на заводе № 1, если она оказалась стандартной.
3.25. В тире имеются 5 ружей, вероятности попадания из которых соответственно равны 0,5; 0,6; 0,7; 0,8 и 0,9.
1. Определить вероятность поражения мишени выстрелом из наугад выбранного ружья.
2. Если выстрелом из наугад взятого ружья мишень поражена, то необходимо определить вероятность того, что это было ружье, вероятность попадания из которого равна 0,9.
3.26. Для сигнализации о том, что режим работы автоматической линии отклоняется от нормального, используются индикаторы двух типов. Вероятности того, что индикатор принадлежит к одному из двух типов, равны 0,4 и 0,6 соответственно. При нарушении работы линии вероятность срабатывания индикатора первого типа равна 0,9, второго типа – 0,7.
1. Найти вероятность того, что наугад выбранный индикатор сработает при нарушении нормальной работы линии.
2. Если индикатор сработал, то следует определить, к какому типу он вероятнее всего принадлежит.
3.27. С применением микромодулей монтируется 20 % приборов, остальные – с применением интегральных схем. Надежность прибора с применением микромодулей равна 0,9, интегральных схем – 0,8.
Найти: а) вероятность надежной работы наугад взятого прибора;
б) вероятность того, что прибор был смонтирован с микромодулем, если он оказался исправным.
3.28. Заготовка может поступить для обработки на один из двух станков с вероятностями 0,4 и 0,6 соответственно. При обработке на первом станке вероятность получения бракованной продукции составляет 0,02, на втором – 0,03.
1. Найти вероятность того, что выбранное случайным образом после обработки изделие окажется стандартным.
2. Если наугад взятое после обработки изделие оказалось стандартным, то следует найти вероятность того, что оно обрабатывалось на первом станке.
3.29. Пассажир может обратиться за получением билета на одну из трех касс вокзала А или в одну из пяти касс вокзала В. Вероятность того, что к моменту прихода пассажира в кассах вокзала А имеются в продаже билеты, равна 0,6, для касс вокзала В эта вероятность равна 0,5.
1. Выяснить, какова вероятность того, что пассажир сможет купить билет в наугад выбранной кассе.
2. Если пассажир приобрел билет, то необходимо определить вероятность того, что он куплен в кассе вокзала А.
3.30. Детали попадают на обработку на один из трех станков с вероятностями, равными 0,2, 0,3, 0,5 соответственно. Вероятность брака на первом станке равна 0,02, на втором – 0,03, на третьем – 0,01.
Найти: а) вероятность того, что случайно взятая после обработки деталь окажется стандартной; б) вероятность обработки наугад взятой детали на втором станке, если она оказалась стандартной.
Задание 4. Решить следующие задачи:
4.1. В семье четверо детей. Принимая равновероятностными событиями рождение мальчика или девочки, найти вероятность того, что мальчиков в семье: а) три; б) не менее трех.
4.2. Всхожесть семян некоторого растения составляет 80 %.
Определить, какова вероятность того, что из семи посеянных семян взойдут: а) три; б) не менее трех.
4.3. Вероятность попадания в цель при одном выстреле из винтовки равна 0,3. Произведено 6 выстрелов.
Найти вероятность того, что произошло: а) три попадания в цель; б) не менее пяти попаданий.
4.4. При передаче сообщения вероятность искажения каждого знака равна 0,1.
Найти вероятность того, что сообщение из десяти знаков: а) не будет искажено; б) содержит не более трех искажений.
4.5. При массовом производстве полупроводниковых диодов вероятность получения брака при формовке равна 0,1.
Найти вероятность того, что среди восьми диодов, проверяемых ОТК, окажется: а) 2 бракованных; б) не более двух бракованных.
4.6. Вероятность потопить судно одной торпедой равна 0,2. Выпущено 5 торпед.
Какова вероятность того, что имеет место: а) 3 попадания в судно; б) не менее трех попаданий?
4.7. Вероятность успешной сдачи студентом каждого из пяти экзаменов равна 0,7.
Рассчитать вероятность успешной сдачи: а) только трех экзаменов; б) не менее двух экзаменов.
4.8. Вероятность поражения мишени данным стрелком при одном выстреле в среднем составляет 80 %. Стрелок производит 6 выстрелов.
Найти вероятность того, что мишень будет поражена: а) 5 раз;
б) не менее пяти раз.
4.9. Вероятность поражения цели каждым из семи выстрелов равна 0,8.
Определить вероятность поражения цели: а) двумя выстрелами;
б) хотя бы одним выстрелом.
4.10. Среди заготовок, изготавливаемых рабочим, в среднем 4 % не удовлетворяют требованиям стандарта.
Найти вероятность того, что среди шести заготовок, взятых для контроля, требованиям стандарта не удовлетворяют: а) не более двух заготовок; б) две заготовки.
4.11. В партии хлопка около 20 % коротких волокон.
Какова вероятность того, что при случайном отборе десяти волокон число коротких будет: а) равно трем; б) не более трех?
4.12. Вероятность того, что изделие пройдет контроль, равна 0,8.
Найти вероятность того, что из шести изделий контроль пройдут: а) 5 изделий; б) не менее пяти изделий.
4.13. Всхожесть семян лимона составляет 80 %.
Найти вероятность того, что из девяти посеянных семян взойдут:
а) 7 семян; б) более семи.
4.14. Вероятность поражения цели при одном выстреле равна 0,8. Произведено 7 выстрелов.
Найти вероятность того, что имело место: а) 6 поражений цели;
б) не более шести поражений.
4.15. Продукция, поступающая из цеха в ОТК, не удовлетворяет условиям стандарта в среднем в 8 % случаев.
Найти вероятность того, что из наугад взятых семи изделий число изделий, которые не удовлетворяют условиям стандарта, будет равно:
а) 6 изделий; б) не менее шести изделий.
4.16. Контрольное задание состоит из пяти вопросов, на каждый из которых дается 4 варианта ответа.
Выяснить, какова вероятность того, что учащийся, не знающий ответов ни на один из вопросов и выбирающий их наугад, даст:
а) 3 правильных ответа; б) не менее трех правильных ответов?
4.17. При игре с определенным противником вероятность выигрыша в каждой шахматной партии для данного игрока равна 0,5.
Найти вероятность того, что он выиграет у этого противника в серии из шести партий: а) хотя бы один раз; б) 3 раза.
4.18. После зубофрезеровки шестерен у рабочего в среднем получается 20 % нестандартных шестерен.
Найти вероятность того, что среди взятых шести шестерен нестандартных будет: а) 3 шестерни; б) не более трех.
4.19. В результате наблюдений, продолжавшихся многие годы, установлено, что на каждую тысячу новорожденных приходится в среднем 515 мальчиков и 485 девочек. В некоторой семье шестеро детей.
Определить, какова вероятность того, что среди них: а) 3 девочки; б) не менее двух девочек.
4.20. Контрольное задание состоит из десяти вопросов, предусматривающих ответы “да” или “нет”. Предположим, учащийся не знает ответ ни на один из вопросов и выбирает ответы наугад.
Найти вероятность того, что он даст: а) не менее восьми правильных ответов, необходимых для зачета задания; б) только 6 правильных ответов.
4.21. Оптовая база обслуживает 6 магазинов. Вероятность получения заявки базой на данный день для каждого из магазинов равна 0,6.
Найти вероятность того, что в этот день будет: а) 5 заявок; б) не менее пяти заявок.
4.22. Вероятность того, что изделие успешно пройдет контроль, равна 0,8.
Найти вероятность того, что из шести выбранных наугад изделий контроль пройдут: а) не менее пяти изделий; б) не более пяти изделий.
4.23. Транзисторный радиоприемник смонтирован на девяти полупроводниках, для каждого из которых вероятность наличия брака равна 0,05.
Какова вероятность того, что: а) хотя бы один из полупроводников будет бракованным; б) приемник будет содержать не менее двух бракованных полупроводников?
4.24. Среди изделий, подвергавшихся термической обработке, в среднем 80 % – высшего сорта.
Найти вероятность того, что среди пяти изделий: а) хотя бы 4 высшего сорта; б) 4 высшего сорта.
4.25. Среди деталей, изготавливаемых рабочим, в среднем 4 % бракованных.
Выяснить, какова вероятность того, что среди взятых на контроль пяти деталей окажутся: а) две бракованные; б) не более одной бракованной.
4.26. Волокна хлопка определенного сорта, в среднем на 75 % имеют длину, меньшую 45 мм, и на 25 % – большую или равную
45 мм. Наугад выбираются 10 волокон.
Найти вероятность того, что среди выбранных волокон: а) не менее трех имеют длину, большую или равную 45 мм; б) не более одного волокна имеет длину больше, чем 45 мм?
4.27. В телеателье имеется 7 телевизоров. Для каждого телевизора вероятность того, что в данный момент он включен, равна 0,6.
Найти вероятность того, что в данный момент включены: а) 4 телевизора; б) хотя бы один телевизор.
4.28. При штамповке изделий бывает в среднем 20 % брака. Для контроля отобрано 8 изделий.
Какова вероятность того, что: а) не менее двух изделий окажутся бракованными; б) только одно изделие бракованное?
4.29. В автопарке предприятия имеется 12 автомашин. Известно, что для каждого из автомобилей вероятность работы без простоев из-за ремонта в течение месяца равна 0,7.
Найти вероятность того, что в течение ближайшего месяца проработают без простоев: а) не менее 10 автомашин; б) не более двух машин.
4.30. Вероятность сдачи экзамена для каждого из шести студентов равна 0,8.
Определить, какова вероятность того, что экзамен сдадут: а) 5 студентов; б) не менее пяти студентов.
Задание 5. Решить следующие задачи:
5.1. Вероятность производства бракованной детали равна 0,08.
Найти вероятность того, что среди взятых на проверку 1000 деталей окажутся: а) 100 бракованных; б) не более 100 бракованных.
5.2. Станок состоит из 2000 независимо работающих узлов. Вероятность отказа одного узла в течение года равна 0,5.
Какова вероятность отказа в течение года: а) 150 узлов; б) не более 50 узлов?
5.3. Вероятность появления события А в каждом из 2100 независимых испытаний равна 0,7.
Рассчитать вероятность того, что событие А наступит: а) не менее 1470 раз и не более 1500 раз; б) ровно 120 раз.
5.4. Вероятность нарушения стандарта при штамповке карболитовых колец равна 0,3.
Найти вероятность того, что для 800 заготовок число бракованных колец: а) окажется равным 240; б) будет заключено между 225 и 250.
5.5. Всхожесть семян оценивается вероятностью 0,85.
Найти вероятность того, что из 500 высеянных семян взойдет:
а) 425 семян; б) от 425 до 450 семян.
5.6. Средний процент нарушения работы кинескопа телевизора в течение гарантийного срока равен 12.
Вычислить вероятность того, что из 460 наблюдаемых телевизоров: а) более 360 отработают гарантийный срок; б) ровно 400 будут работать без сбоя.
5.7. Известно, что при посадке деревьев определенного вида приживается 80 % саженцев.
Найти вероятность того, что из 400 посаженных деревьев: а) приживутся ровно 300; б) приживутся не менее 300.
5.8. Вероятность поражения мишени при одном выстреле равна 0,8.
Выяснить, какова вероятность того, что в серии из 100 выстрелов мишень будет поражена: а) ровно 90 раз; б) не менее 75 раз.
5.9. Вероятность появления события А в каждом из 2000 независимых испытаний равна 0,7.
Найти вероятность того, что событие А наступит: а) не менее 1500 раз; б) ровно 1000 раз.
5.10. Вероятность рождения мальчика равна 0,515.
Определить вероятность того, что среди 1000 рождающихся детей: а) будет ровно половина мальчиков; б) мальчиков будет не менее 500 и не более 550.
5.11. Всхожесть семян данного растения равна 0,9.
Найти вероятность того, что среди 900 посаженных семян число проросших будет равно: а) 800; б) не менее 790 и не более 830.
5.12. Вероятность поражения мишени при одном выстреле равна 0,85.
Какова вероятность того, что при 50 выстрелах мишень будет поражена: а) не менее 35 раз; б) 40 раз?
5.13. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,4.
Найти вероятность того, что в течение 1 мин обрыв произойдет:
а) на 60 веретенах; б) не менее чем на 50 веретенах.
5.14. Вероятность отклонений от принятого стандарта при штамповке клемм равна 0,02.
Вычислить вероятность наличия в партии из 200 клемм: а) ровно 50 клемм, не соответствующих стандарту; б) не более 40 нестандартных клемм.
5.15. Посажено 600 семян кукурузы. Вероятность прорастания для каждого из семян равна 0,9.
Определить вероятность того, что число проросших семян: а) больше 400; б) равно 500.
5.16. Вероятность того, что пара обуви, взятая из изготовленной партии, окажется высшего сорта, равна 0,4. На контроль поступило 600 пар обуви.
Найти вероятность того, что число пар обуви высшего сорта будет: а) от 228 до 252 включительно; б) равно 300.
5.17. Вероятность поражения мишени при одном выстреле равна 0,8.
Рассчитать вероятность поражения мишени: а) 75 раз в серии из 100 выстрелов; б) не менее 75 раз при 100 выстрелах.
5.18. Прядильщица обслуживает 2000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,04.
Определить, какова вероятность того, что в течение 1 мин обрыв произойдет: а) на 100 веретенах; б) не более, чем на 150 веретенах.
5.19. Вероятность остановки в течение часа каждой из 100 работающих машин равна 0,2.
Найти вероятность остановки в течение ближайшего часа работы:
а) 30 машин; б) не менее 20 машин.
5.20. В передаваемой по каналу связи последовательности знаков, образующих сообщение, любой знак из-за помех, независимо от других, искажается с вероятностью 0,2.
Найти вероятность того, что в переданной последовательности из 1000 знаков число искажений будет равно: а) не менее 100; б) не более 200.
5.21. Вероятность того, что выбранное изделие окажется высшего сорта, равна 0,5.
Найти вероятность того, что из 1000 изделий число изделий высшего сорта будет равно: а) 500; б) не менее 300.
5.22. Промышленная телевизионная установка содержит 2000 транзисторов. В течение гарантийного срока вероятность выхода из строя каждого из транзисторов равна 0,05.
Определить, какова вероятность выхода из строя в течение гарантийного срока: а) хотя бы одного транзистора; б) не менее 30 транзисторов.
5.23. Вероятность того, что на странице книги могут оказаться опечатки, равна 0,2. Проверяется книга, содержащая 500 страниц.
Найти вероятность того, что с опечатками окажутся: а) 50 страниц; б) не более 50 страниц.
5.24. Автоматическая штамповка клемм для предохранителей дает 10 % отклонений от принятого стандарта.
Найти вероятность того, что среди 400 клемм число стандартных будет равно: а) 90; б) не менее 100.
5.25. Из всех изготавливаемых на заводе кинескопов для телевизоров 20 % не выдерживают гарантийный срок службы.
Найти вероятность того, что в партии из 600 кинескопов число не выдержавших этот срок будет равно: а) 115; б) заключено в промежутке между 100 и 125.
5.26. На заводе работают 500 человек. Для каждого из рабочих вероятность невыхода из-за болезни в определенный день равна 0,1.
Какова вероятность того, что число отсутствующих будет равно:
а) не более 40; б) 50 человек?
5.27. Всхожесть семян данного растения равна 0,9.
Найти вероятность того, что из 900 посаженных семян число проросших будет: а) заключено между 790 и 830; б) 800 семян.
5.28. Мастерская по гарантийному ремонту телевизоров обслуживает 2000 абонентов. Для каждого из купленных телевизоров вероятность поломки в течение гарантийного срока равна 0,3.
Найти вероятность того, что гарантийного ремонта потребуют:
а) не более 550 телевизоров; б) 800 телевизоров.
5.29. Аппаратура состоит из 1000 элементов. Для каждого из элементов вероятность отказа в течение времени t равна 0,1 и не зависит от работы других элементов.
Найти вероятность отказа в течение времени t: а) 100 элементов;
б) не менее 150 элементов.
5.30. Производство изделий дает 1 % брака.
Какова вероятность того, что из взятых на исследование 1100 изделий бракованных будет: а) не более 17; б) ровно 20 изделий?
Задание 6. Для определенной в условии задачи дискретной случайной величины необходимо выполнить следующее:
1. Построить ряд распределения и многоугольник распределения.
2. Найти функцию распределения и построить ее график.
3. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
6.1. Среди 10 лотерейных билетов имеется 6 билетов с выигрышем. Наудачу покупают 4 билета. Случайная величина X – число выигрышных билетов среди купленных.
6.2. Баскетболист делает 3 штрафных броска. Вероятность попадания при каждом броске равна 0,7. Случайная величина X – число попаданий мяча в корзину.
6.3. В партии из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Случайная величина X – число дефектных курток среди купленных.
6.4. Вероятность того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3. Аудитору на заключение представлено 3 баланса предприятия. Случайная величина X – число положительных заключений на проверяемые балансы.
6.5. Вероятность сбоя в работе АТС равна 0,1. Поступило 5 вызовов. Случайная величина X – число сбоев в работе АТС.
6.6. Партия содержит 20 телевизоров, среди которых 6 имеет дефект. Купили 3 телевизора. Случайная величина X – число исправленных телевизоров среди купленных.
6.7. Производится 3 независимых измерения исследуемого образца. Вероятность допустить ошибку в каждом измерении равна 0,05. Случайная величина X – число ошибок, допущенных в измерениях.
6.8. На пути движения автомашины 4 светофора. Каждый из них либо разрешает, либо запрещает автомашине дальнейшее движение с вероятностью 0,5. Случайная величина X – число светофоров, пройденных машиной без остановки.
6.9. При установившемся технологическом процессе предприятие выпускает 2/3 своих изделий первым сортом и 1/3 – вторым. Случайная величина X – число изделий первого сорта среди взятых наугад четырех изделий.
6.10. Из партии в количестве 20 изделий, среди которых имеется
6 бракованных. Для проверки качества случайным образом выбраны 3 изделия. Случайная величина X – число бракованных изделий среди отобранных.
6.11. Вероятность успешной сдачи данного экзамена для каждого из четырех студентов равна 0,8. Случайная величина X – число студентов, успешно сдавших экзамен.
6.12. В урне 20 шаров, из них 6 имеют дефект. Наудачу отбирают
4 шара. Случайная величина X – число бездефектных шаров среди отобранных.
6.13. Товаровед осматривает 10 изделий. Вероятность появления бракованного изделия в партии равна 0,2. Случайная величина X – число появлений стандартных изделий в партии.
6.14. Студент знает 40 из 50 вопросов программы. Случайная величина X – число правильных ответов на предложенные 3 вопроса курса.
6.15. В урне 5 красных и 4 синих шаров. Отбирают 3 шара. Случайная величина X – число шаров красного цвета среди отобранных.
6.16. Вероятность рождения мальчика равна 0,51. Случайная величина X – количество мальчиков в семье из четырех детей.
6.17. В партии 8 деталей, из которых 4 – стандартные. Наудачу отобрано 4 детали. Случайная величина X – число стандартных деталей среди отобранных.
6.18. Студент знает 20 из 25 вопросов. Случайная величина X – число правильных ответов на предложенные четыре вопроса программы курса.
6.19. В урне 15 шаров, из них 5 – красных, 10 – белых и 5 – зеленых. Наудачу отбирают 3 шара. Случайная величина X – число красных шаров среди отобранных.
6.20. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Случайная величина X – число попаданий при четырех выстрелах.
6.21. В ящике содержатся 10 деталей, из которых 4 окрашены. Сборщик наудачу берет 3 детали. Случайная величина X – число окрашенных деталей среди отобранных.
6.22. В группе 20 студентов, из них 40 % юношей. Вызывают
5 студентов одновременно. Случайная величина X – число юношей среди вызванных студентов.
6.23. В урне 15 шаров, среди которых 10 красных. Наудачу извлекают 4 шара. Случайная величина X – число красных шаров среди отобранных.
6.24. Монету бросают 6 раз. Случайная величина X – число появления герба.
6.25. Партия из 20 изделий содержит 5 бракованных. Из партии выбирают 5 изделий. Случайная величина X – число бракованных изделий, содержащихся в случайной выборке.
6.26. В урне 10 шаров, из которых 8 окрашены. Наудачу отобраны 3 шара. Случайная величина X – число окрашенных шаров в случайной выборке.
6.27. Вероятность отказа элементов некоторого устройства рав-
на 0,9. Случайная величина X – число отказов элементов устройства в пяти независимых испытаниях.
6.28. Из урны, содержащей 5 белых и 3 черных шара, наугад извлекают 4 шара. Случайная величина X – число вынутых белых шаров.
6.29. Имеется 3 базы с независимым снабжением. Вероятность отсутствия на базе нужного товара равна 0,1. Предприниматель решил закупить мелкий товар. Случайная величина X – число баз, на которых в данный момент этот товар отсутствует.
6.30. Бросают 4 игральные кости. Случайная величина X – число выпадения одного очка.
Задание 7. Закон распределения непрерывной случайной величины задан функцией распределения вероятностей F (x).
Требуется выполнить следующее:
1. Найти функцию плотности распределения данной случайной величины f (x).
2. Построить графики функций F (x) и f (x).
3. Вычислить математическое ожидание, дисперсию и среднее кадратическое отклонение случайной величины.
4. Найти вероятность того, что данная случайная величина примет значение, принадлежащее отрезку [ a; b ].
7.1. 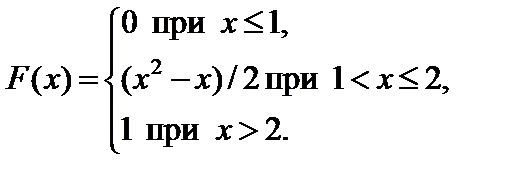 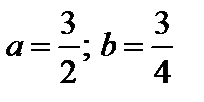 . . | 7.2. 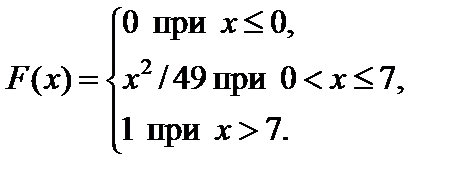 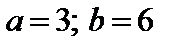 . . |
7.3. 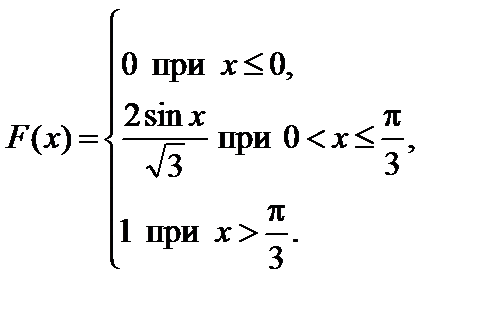 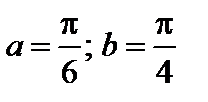 . . | 7.4. 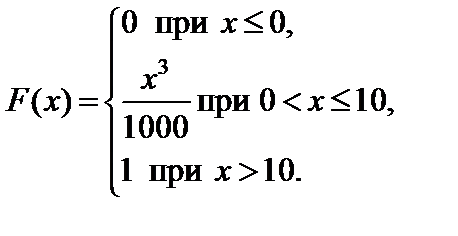 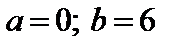 . . |
7.5. 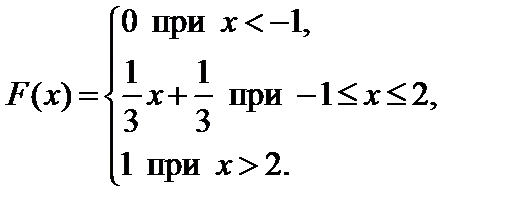 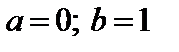 . . | 7.6. 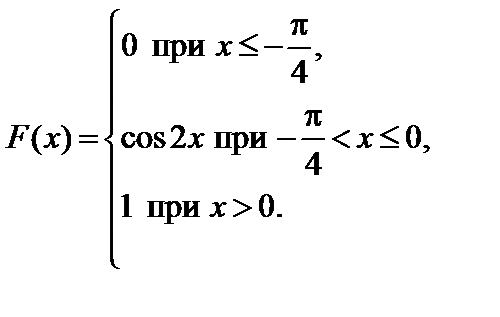 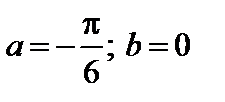 . . |
7.7. 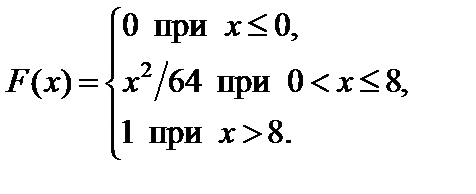 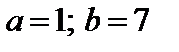 . . | 7.8. 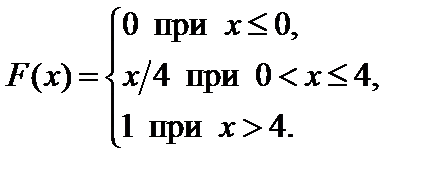 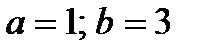 . . |
7.9. 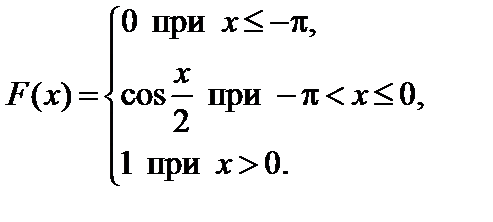 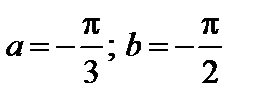 . . | 7.10. 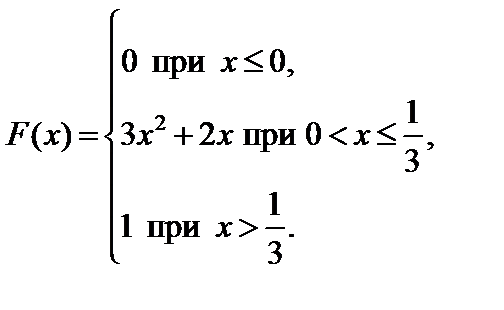 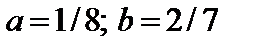 . . |
7.11. 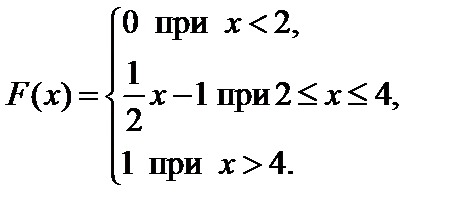 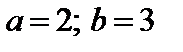 . . | 7.12. 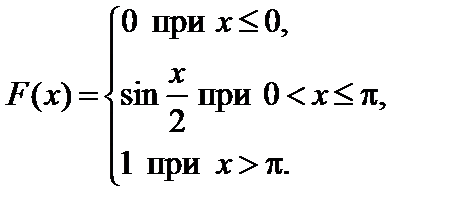 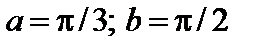 . . |
7.13. 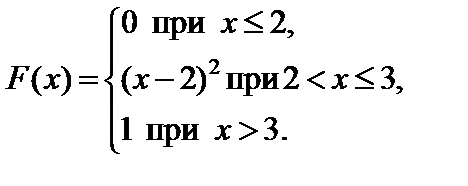 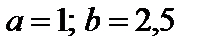 . . | 7.14. 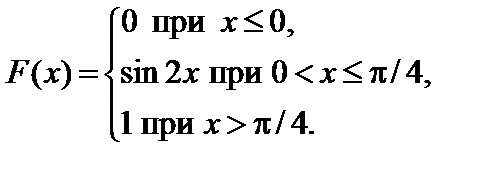 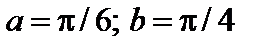 . . |
7.15.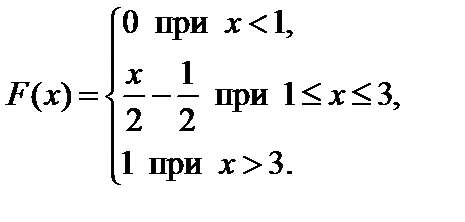 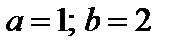 . . | 7.16. 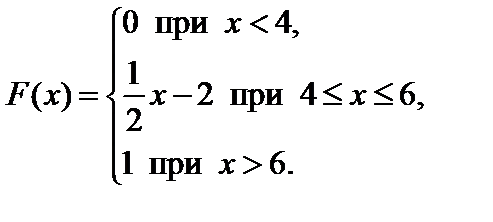 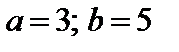 . . |
7.17.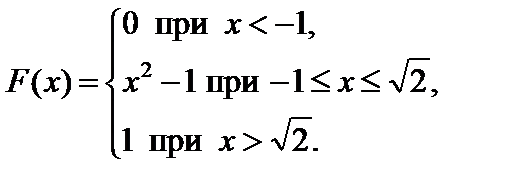 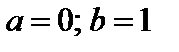 . . | 7.18. 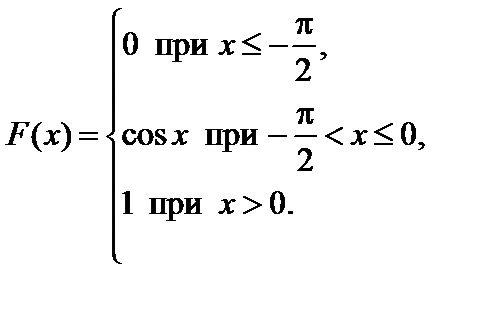 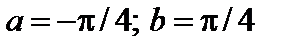 . . |
7.19. 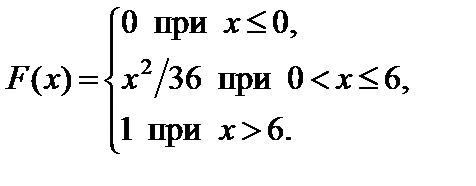 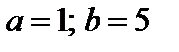 . . | 7.20. 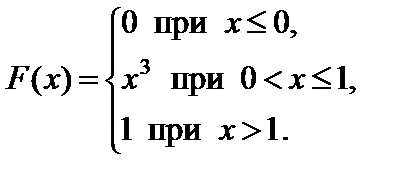 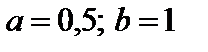 . . |
7.21. 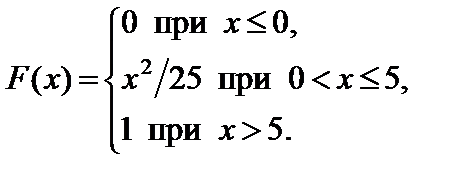 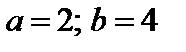 . . | 7.22. 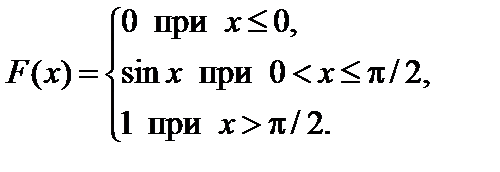 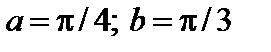 . . |
7.23.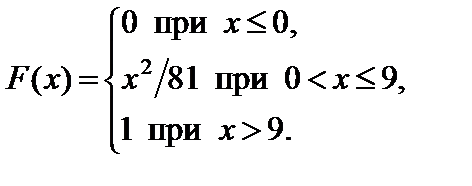 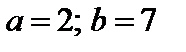 . . | 7.24. 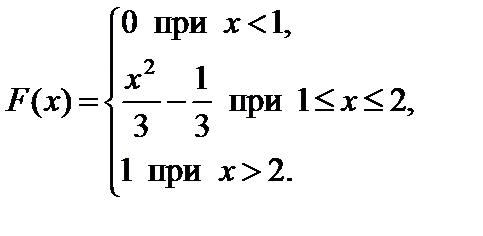 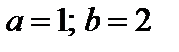 . . |
7.25. 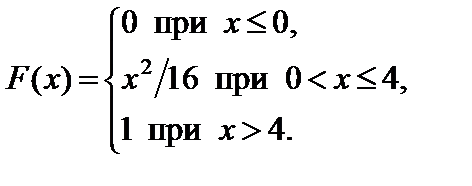 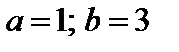 . . | 7.26.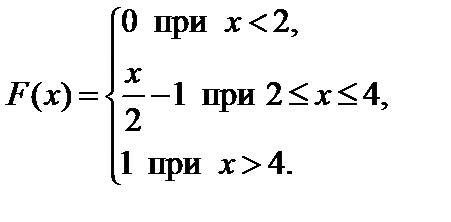 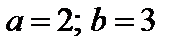 . . |
7.27. 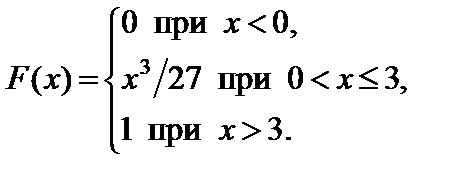 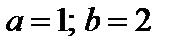 . . | 7.28.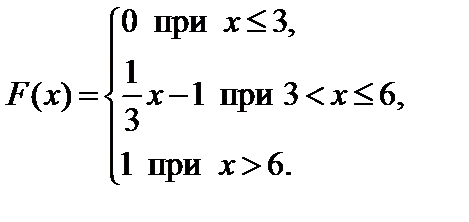 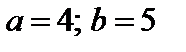 . . |
7.29. 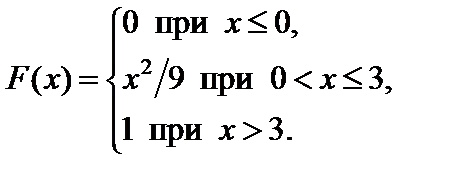 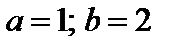 . . | 7.30. 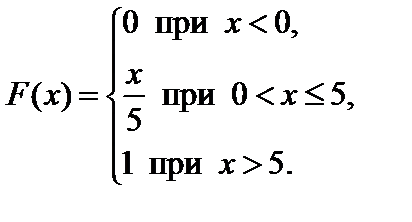 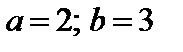 . . |
Задание 8. Решить следующие задачи:
8.1. Измерительный прибор имеет систематическую ошибку, равную 5 м, и среднее квадратическое отклонение случайной ошибки – 75 м. Возникающие ошибки распределены по нормальному закону. Найти вероятность того, что ошибка измерения не превзойдет по абсолютной величине 5 м.
8.2. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х равны 12 и
2 соответственно. Найти вероятность того, что случайная величина Х примет значение, заключенное в интервале (14; 16).
8.3. Производят взвешивание вещества без систематических ошибок. Случайная ошибка взвешивания распределена нормально с математическим ожиданием, равным 20 кг и средним квадратическим отклонением – 2 кг. Найти вероятность того, что следующее взвешивание отличается от математического ожидания не более, чем на 10 г.
8.4. Детали, выпускаемые цехом, имеют диаметры, которые распределены по нормальному закону с математическим ожиданием, равным 5 см, и дисперсией – 0,81 см2. Найти вероятность того, что диаметр наугад взятой детали имеет размер от 4 до 7 см.
8.5. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна
50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением, равным 100 м. Рассчитать вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м.
8.6. Случайная величина Х распределена по нормальному закону, математическое ожидание равно 20, а среднее квадратическое отклонение – 3. Найти симметричный относительно математического ожидания интервал, в который с вероятностью 0,9972 попадет случайная величина Х.
8.7. Станок-автомат изготавливает валики, причем контролируется их диаметр Х. Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 10 мм, и средним квадратическим отклонением 0,1 мм. Найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.
8.8. Случайная величина Х подчинена нормальному закону с математическим ожиданием, равным 0. Вероятность попадания этой случайной величины в интервал (–1; 1) равна 0,5. Найти среднее квадратическое отклонение и записать нормальный закон распределения случайной величины Х.
8.9. Известно, что средний расход удобрений на один гектар пашни составляет 80 кг, а среднее квадратическое отклонение расхода равно 5 кг. Считая расход удобрений нормально распределенной случайной величиной, определить диапазон, в который вносимая доза удобрений попадает с вероятностью 0,98.
8.10. При взвешивании на весах допускаются случайные ошибки с дисперсией, равной 100 г2, и систематической ошибкой, равной 20 г. Полагая, что ошибки распределены по нормальному закону, определить вероятность того, что ошибка при взвешивании предмета по абсолютной величине не превысит 50 г.
8.11. При определении расстояния радиолокатором случайные ошибки распределяются по нормальному закону. Найти вероятность того, что ошибка при определении расстояния не превысит 20 м, если известно, что систематических ошибок радиолокатор не допускает, а дисперсия случайных ошибок равна 1370 м2.
8.12. Случайная величина Х нормально распределена с математическим ожиданием, равным 40, и дисперсией, равной 100. Вычислить вероятность попадания случайной величины Х в интервал (30; 80).
8.13. Математическое ожидание нормально распределенной случайной величины Х (количество сыра, используемого для изготовления 100 бутербродов), равно 1 кг. Расход сыра на изготовление
100 бутербродов составляет от 900 до 1100 г с вероятностью 0,96. Определить среднее квадратическое отклонение расхода сыра на 100 бутербродов.
8.14. Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 10. Вероятность попадания Х в интервал (10; 20) равна 0,3. Найти вероятность попадания случайной величины Х в интервал (0; 10).
8.15. Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 10, и средним квадратическим отклонением, равным 5. Найти интервал, в который попадет случайная величина Х в результате испытания с вероятностью 0,9973.
8.16. Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 25. Вероятность попадания Х в интервал (10; 15) равна 0,2. Найти вероятность попадания случайной виличины Х в интервал (35; 40).
8.17. Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 15, и средним квадратическим отклонением, равным 2. Найти симметричный относительно математического ожидания интервал, в который попадет случайная величина Х с вероятностью 0,954.
8.18. Случайная величина Х распределена по нормальному закону со средним квадратическим отклонением, равным 5 мм, и математическим ожиданием, равным 15. Найти длину интервала, в который попадет случайная величина Х в результате испытания с вероятностью 0,9973.
8.19. Случайная величина Х распределена по нормальному закону со средним квадратическим отклонением, равным 5. Найти длину интервала, симметричного относительно математического ожидания, в который попадет случайная величина Х в результате испытания с вероятностью 0,9973.
8.20. Случайная величина Х (ошибка измерения) распределена по нормальному закону с математическим ожиданием, равным 0, и средним квадратическим отклонением, равным 3. Найти вероятность того, что случайная величина Х попадет в интервал (–9; 9).
8.21. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х равны 20 и 5 соответственно. Найти вероятность того, что в результате испытания случайная величина Х примет значение, заключенное в интервале (15; 25).
8.22. Автомат изготавливает шарики. Шарик считается стандартным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Случайная величина Х распределена по нормальному закону со средним квадратическим отклонением, равным 0,4 мм. Найти количество стандартных шариков среди 100 изготовленных.
8.23. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону
 2015-04-20
2015-04-20 3654
3654
