Как говорилось выше, вычисление интеграла  равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = b и «боковыми сторонами» y = 0, y = f (x) (рис. 14).
равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = b и «боковыми сторонами» y = 0, y = f (x) (рис. 14).
Разобьем интервал интегрирования на n равных частей, каждая длиной  .
.
Приближенное значение интеграла получается в виде суммы площадей n прямоугольников, высота которых равна значению f(x) на левом краю каждого подинтервала (рис. 3).

 hy 0 +hy 1 +…+hyn- 1 = h (y 0 +y 1 +…+yn- 1). То есть формула численного интегрирования имеет вид:
hy 0 +hy 1 +…+hyn- 1 = h (y 0 +y 1 +…+yn- 1). То есть формула численного интегрирования имеет вид:
 (4)
(4)
и называется формулой «левых» прямоугольников.
Рисунок 16 – Геометрическая интерпретация метода «левых» прямоугольников
Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f(x) на правом краю подинтервала (рис. 4), то формула численного интегрирования имеет вид (5):
 (5)
(5)
и называется формулой «правых» прямоугольников.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA8tqz2cUA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPT2vCQBTE7wW/w/IEb3WjgtTUVfyDIlYFrZfeXrPP JJh9G7Krid/eLRQ8DjPzG2Y8bUwh7lS53LKCXjcCQZxYnXOq4Py9ev8A4TyyxsIyKXiQg+mk9TbG WNuaj3Q/+VQECLsYFWTel7GULsnIoOvakjh4F1sZ9EFWqdQV1gFuCtmPoqE0mHNYyLCkRUbJ9XQz Cn62KzvffzXL884NebauD8dfvCnVaTezTxCeGv8K/7c3WsFgNIK/M+EIyMkTAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQDy2rPZxQAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f">
Рисунок17 – Геометрическая интерпретация метода «правых» прямоугольников
Существует третья модификация метода прямоугольников – метод «средних» прямоугольников. В этом случае в качестве приближенного значения площади для каждого подинтервала принимается площадь прямоугольника, высота которого равна значению f(x) в средней точке подинтервала (рис. 5).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA9xUFRcYA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE74L/YXmCN92oVCTNKrZiKbUVtLn09pp9 JsHs25BdTfrvu4LgcZiZb5hk1ZlKXKlxpWUFk3EEgjizuuRcQfq9HS1AOI+ssbJMCv7IwWrZ7yUY a9vyga5Hn4sAYRejgsL7OpbSZQUZdGNbEwfvZBuDPsgml7rBNsBNJadRNJcGSw4LBdb0WlB2Pl6M gp+PrX352nWb9NPNef3W7g+/eFFqOOjWzyA8df4RvrfftYLZ0wRuZ8IRkMt/AAAA//8DAFBLAQIt ABQABgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFw ZXhtbC54bWxQSwECLQAUAAYACAAAACEA9xUFRcYAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJz L2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIsDAAAAAA== " filled="f" stroked="f">
Рисунок18 – Геометрическая интерпретация метода «средних» прямоугольников
Тогда формула численного интегрирования имеет вид (6):
 (6)
(6)
Метод прямоугольников – это наиболее простой и вместе с тем наиболее грубый метод приближенного интегрирования. Очевидно, что чем больше будет число n отрезков разбиения, тем более точный результат дадут формулы (4)-(6). Однако увеличение числа отрезков разбиения промежутка интегрирования не всегда возможно. Поэтому большой интерес представляют формулы, дающие более точные результаты при том же числе точек разбиения. Заметно меньшую погрешность дает другой метод – метод трапеций.
Метод трапеций
В этом методе отрезок [ a; b ] так же разбивается на n равных частей. На каждом отрезке [ xi; xi+1 ] кривая y = f(x) заменяется прямой, проходящей через две известные точки с координатами  и
и  , где
, где  и строится прямоугольная трапеция с высотой >
и строится прямоугольная трапеция с высотой >
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA5KYqWMYA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE7wX/w/IEb80mFUTSrKItEWm1oPXS22v2 mYRm34bsatJ/3xWEHoeZ+YbJloNpxJU6V1tWkEQxCOLC6ppLBafP/HEOwnlkjY1lUvBLDpaL0UOG qbY9H+h69KUIEHYpKqi8b1MpXVGRQRfZljh4Z9sZ9EF2pdQd9gFuGvkUxzNpsOawUGFLLxUVP8eL UfD1ltv1/n14Pe3cjFeb/uPwjRelJuNh9QzC0+D/w/f2ViuYxgnczoQjIBd/AAAA//8DAFBLAQIt ABQABgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFw ZXhtbC54bWxQSwECLQAUAAYACAAAACEA5KYqWMYAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJz L2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIsDAAAAAA== " filled="f" stroked="f">
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAv2TVoMUA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPS4vCQBCE7wv+h6EFb+tEXUSio/hAkX0IPi7e2kyb BDM9ITOa+O+dhYU9FlX1FTWZNaYQD6pcbllBrxuBIE6szjlVcDqu30cgnEfWWFgmBU9yMJu23iYY a1vznh4Hn4oAYRejgsz7MpbSJRkZdF1bEgfvaiuDPsgqlbrCOsBNIftRNJQGcw4LGZa0zCi5He5G wflzbRc/X83q9O2GPN/Uu/0F70p12s18DMJT4//Df+2tVjDof8DvmXAE5PQFAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQC/ZNWgxQAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f">

(рис. 19).
Рисунок 19 – Геометрическая интерпретация метода трапеций
В итоге искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических трапеций. (Площадь трапеции с высотой h и основаниями a, b вычисляется по формуле:  ). Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.
). Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.
Тогда 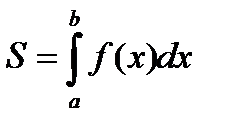


вынесем h за скобку, получим
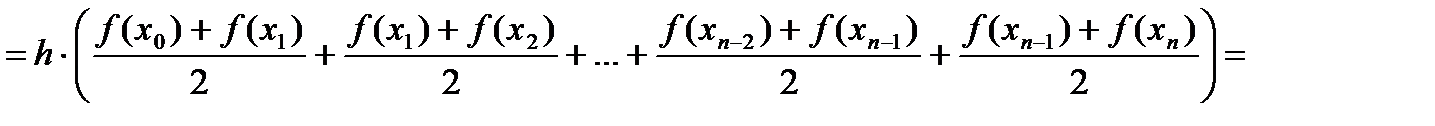
разобьем каждую дробь на две дроби

приведем подобные слагаемые, получим
 .
.
Итак, 

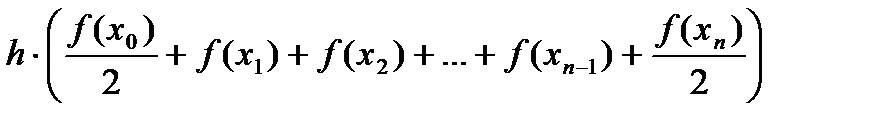 .
.
Коротко полученную формулу можно записать в виде (7).

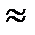
 (7)
(7)
Заметим, что в данном методе получаем ступенчатую фигуру, составленную из трапеций, которая «плотнее» прилегает к заданной криволинейной трапеции, нежели фигура, составленная из прямоугольников в предыдущем методе.
 равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = b и «боковыми сторонами» y = 0, y = f (x) (рис. 14).
равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = b и «боковыми сторонами» y = 0, y = f (x) (рис. 14). .
.
 hy 0 +hy 1 +…+hyn- 1 = h (y 0 +y 1 +…+yn- 1). То есть формула численного интегрирования имеет вид:
hy 0 +hy 1 +…+hyn- 1 = h (y 0 +y 1 +…+yn- 1). То есть формула численного интегрирования имеет вид: (4)
(4) (5)
(5)


 (6)
(6) и
и  , где
, где  и строится прямоугольная трапеция с высотой >
и строится прямоугольная трапеция с высотой >  (рис. 19).
(рис. 19).
 ). Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.
). Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.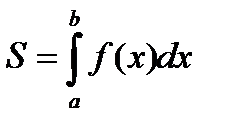


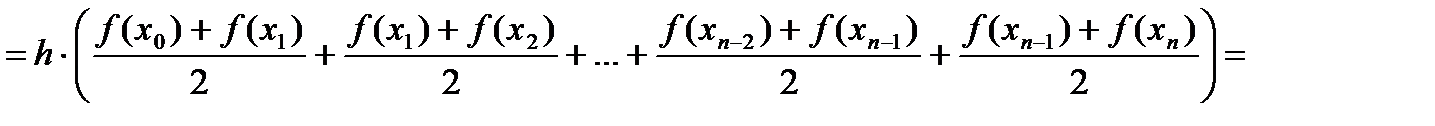

 .
.

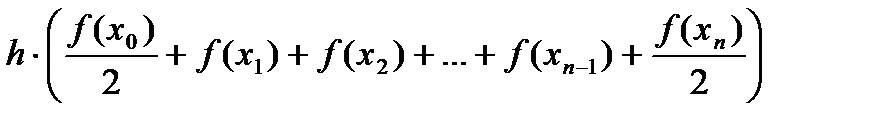 .
.
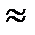
 (7)
(7) 2017-12-14
2017-12-14 960
960








