2017-12-14
2193
Запишем для функции f (x), заданной своими значениями в равноотстоящих узлах 
первый интерполяционный многочлен Ньютона:
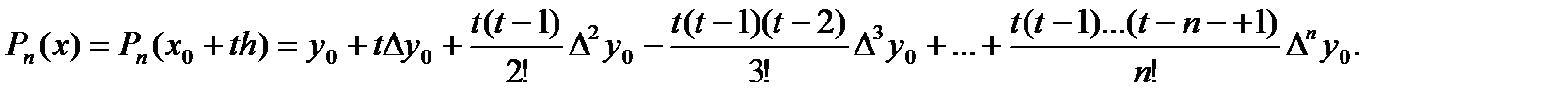Перепишем этот полином, производя перемножение скобок:
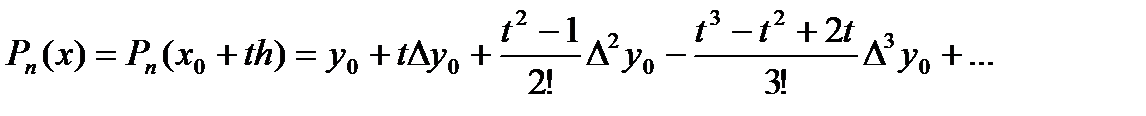
Дифференцируя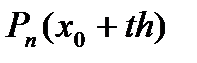 
по t, получим аналогично формуле (9):
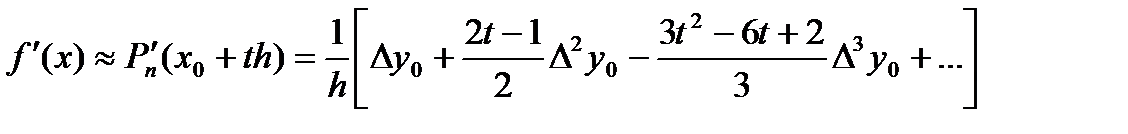(14)
Подобным путём можно получить и производные функции f (x) более высоких порядков. Однако, каждый раз, вычисляя значение производной f (x) в фиксированной точке x, в качестве x 0 следует брать ближайшее слева узловое значение аргумента.
Формула (14) существенно упрощается, если исходным значением xоказывается один из узлов таблицы. Так как в этом случае каждый узел можно считать начальным, то, принимая x = x 0, t =0, получаем:
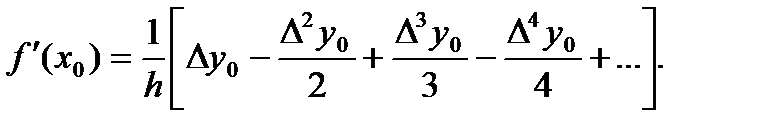(15)
Эта формула позволяет легко и достаточно точно получать значения производных функций, заданных таблично. Воспользуемся для иллюстрации функцией, производная которой (для сопоставления) может быть легко вычислена обычным способом.
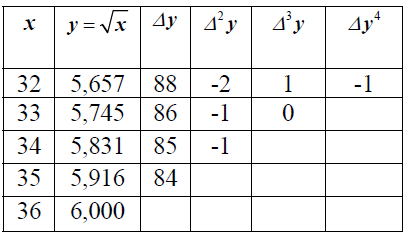
Пример 3. Найти значение производной функции f (x)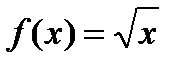 
в точке x = 32, используя таблицу 3. В данном случае h =1; применяя формулу (15) к данным первой строки таблицы (до разностей третьего порядка включительно), получим:
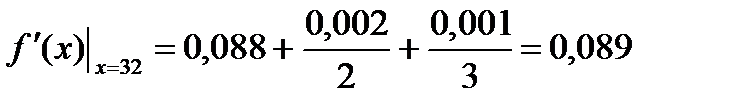
Сопоставляя полученный ответ со значением
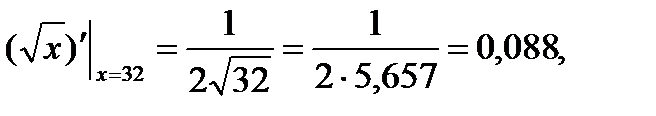
замечаем совпадение значений в пределах двух знаков после запятой.
Используя формулу (10) применительно к первому интерполяционному многочлену Ньютона, запишем:
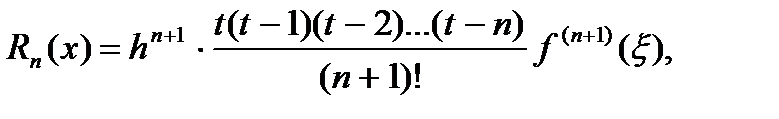
где ξ - некоторое промежуточное значение между узлами и заданной точкой x. Предполагая, что f (x) дифференцируема n +1 раз, получим для оценки погрешности дифференцирования rn (x) (по аналогии с формулой (11)):
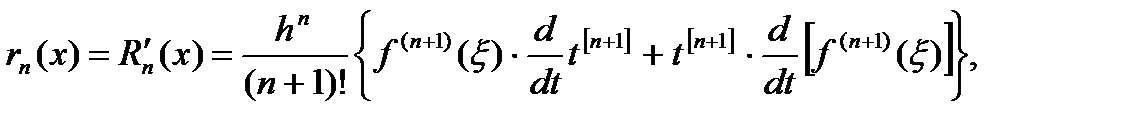(16)
Для случая оценки погрешности в узле таблицы (когда x = x 0и t = 0) будем иметь удобный вид формулы (16):
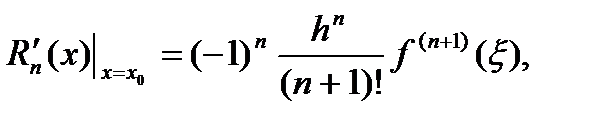
На практике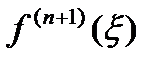 
оценивать непросто, поэтому при малых h приближенно полагают:
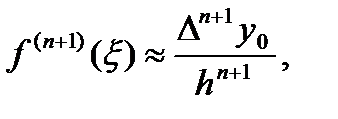
что позволяет использовать приближенную формулу
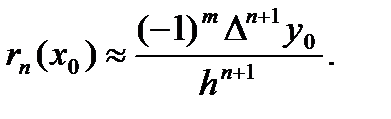(17)
