Техника вычисления простейших пределов

Найти пределы функций:

1а) =(так как функция непрерывна при х=2)=

1б) Разложим числитель и знаменатель на множители.

Получим

в) (Домножим числитель и знаменатель на сумму корней)

г)

Техника нахождения пределов функций на бесконечности.

1)

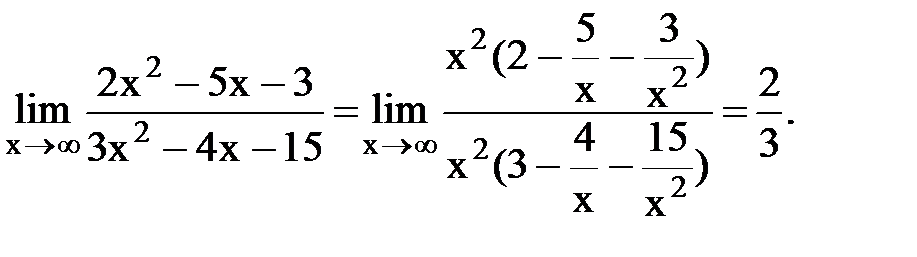
4) Применим второй замечательный предел. Сделаем замену

. Получим

Исследование функции на непрерывность

1. Найти точки разрыва функции, построить график этой функции:

.

Решение

Функция непрерывна в интервалах (-¥, 1), (1, 3), (3,+¥). Проверим функцию на непрерывность в точках х₀=1 и 3. Воспользуемся определением непрерывности функции f(x) в точке х₀

.

1) х₀=1

Следовательно функция непрерывна в точке х₀=1.

2) х₀=3.

Следовательно функция разрывна в точке х₀=3.

 

Сделаем чертеж

2. Найти точки разрыва функции, построить график этой функции

.

 

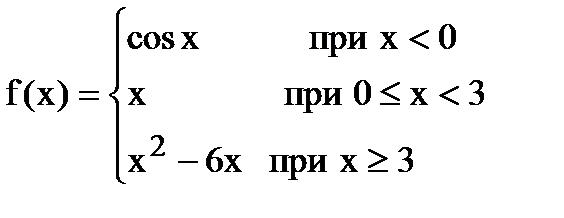Решение

Функция непрерывна в интервалах (-¥, 0), (0, 3), (3,+¥). Проверим функцию на непрерывность в точках х₀=0 и 3. Воспользуемся определением непрерывности функции f(x) в точке х₀

.

1) х₀=0

Следовательно функция разрывна в точке х₀=0.

2) х₀=3.

Следовательно функция разрывна в точке х₀=3.Сделаем чертеж