Вычисление определенного интеграла

Вычислите определенные интегралы а)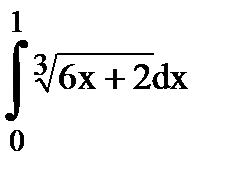

Решение:

 

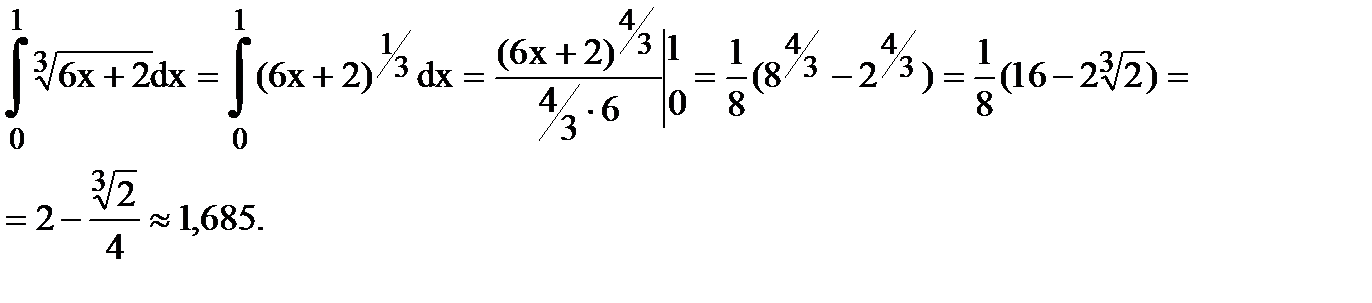
Ответ: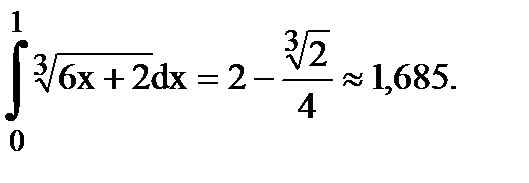

Вычислите определенные интегралы.

c)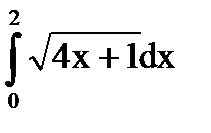

Решение:

 

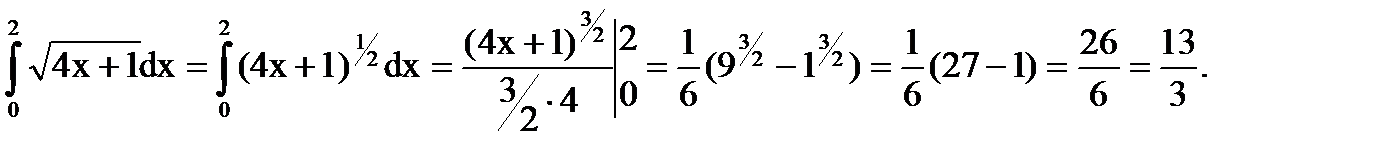
Ответ: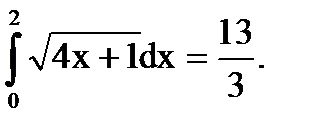

d)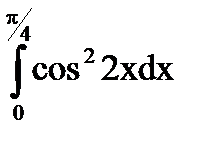

Решение:

Воспользуемся тригонометрической формулой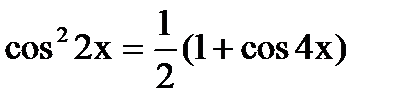

 

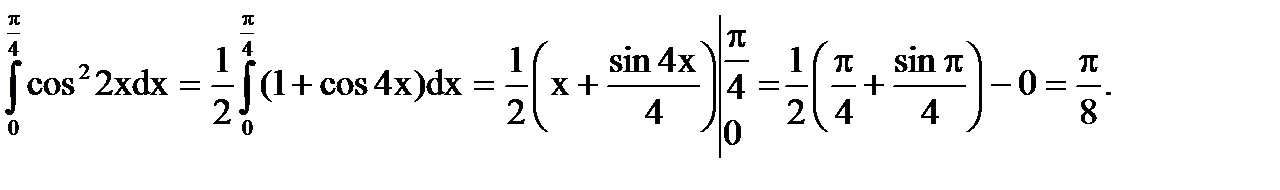
Ответ: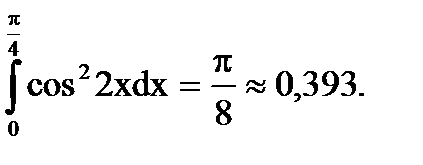

Интегрирование определенного интеграла подстановкой.

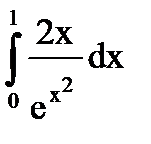
Решение:

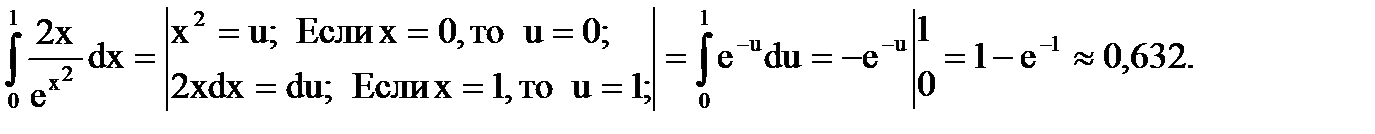
Ответ: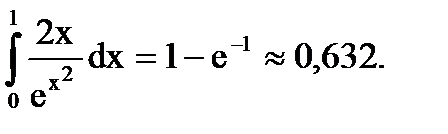

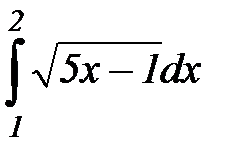
а) 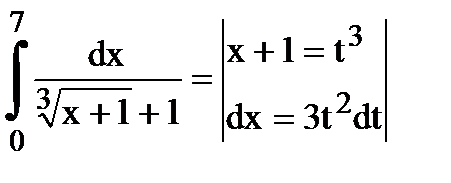= Найдем новые пределы интегрирования =

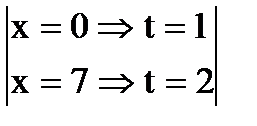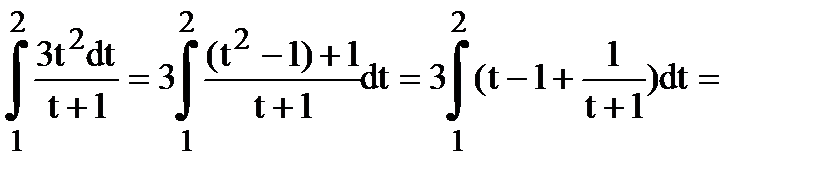
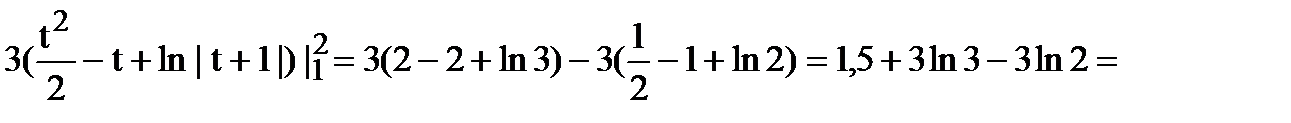
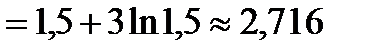
Ответ: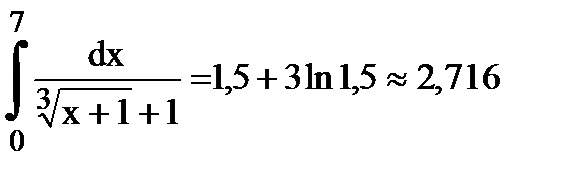

Интегрирование определенного интеграла по «частям»

 

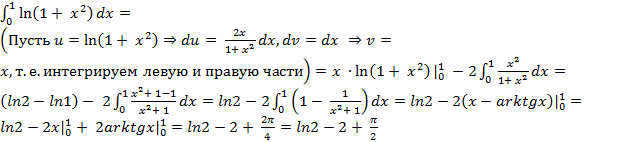
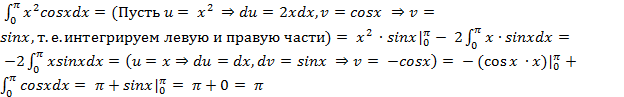
Нахождение площади плоской фигуры.

Найдите площадь фигуры, ограниченной линиями.

y=x²-4 и y=4-x².

Решение:

Обе линии являются параболами.

Вершина первой параболы находится в точке (0; -4). Ветви направлены вверх.

Вершина второй параболы находится в точке (0; 4). Ветви направлены вниз.

Найдем точки пересечения этих линий.

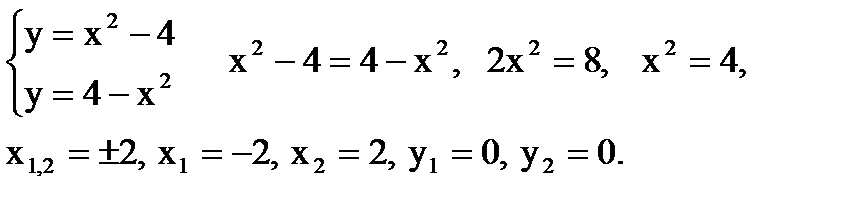
у

Сделаем чертеж:

х

у=4-х2

у=х2-4

Площадь найдем по формуле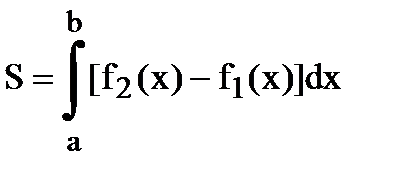

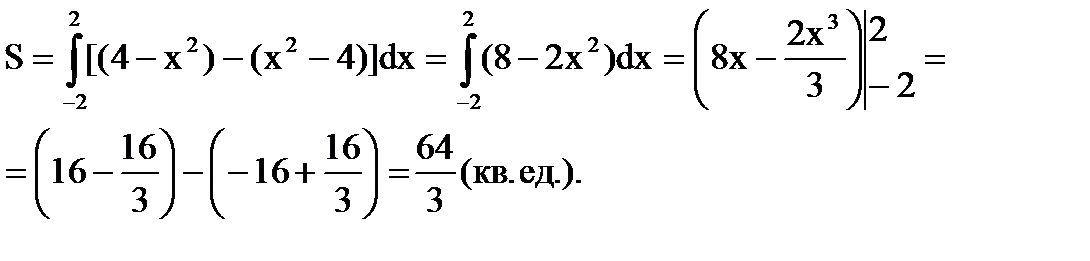
Ответ: Искомая площадь 64/3 (кв. ед.).