Способы задания прямой на плоскости

Пример. Дан треугольник с вершинами А(–2; 0), В(2; 4), С(4; 0). Написать уравнения медианы АЕ, высоты AD и найти длину медианы АЕ.

Решение:

1) Найдем уравнение высоты AD как прямой, проходящей через точку А(–2; 0) перпендикулярно вектору :

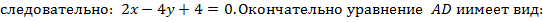
2) Найдем уравнение медианы АЕ как прямой, проходящей через две точки А и Е. Координаты точки Е найдем как координаты середины отрезка СВ:

E(3; 2). Уравнение АЕ:

3) Найдем длину медианы АЕ:

;

, .

Ответ: .

Пример. Даны вершины треугольника , и . Составить уравнения его высот.

Решение:

Пусть - высота треугольника . Рассмотрим два вектора и 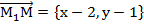. По условию эти векторы ортогональны. Значит, .

Аналогично находим остальные высоты треугольника.

Ответ: .

Пример. Составить уравнения сторон и медиан треугольника с вершинами А(3; 2),B(5; -2), С(1; 0).

Решение:

1) Воспользуемся уравнением прямой, проходящей через две данные точки

;

Найдем уравнение медианы AM. Для этого найдем координаты точки М - середины отрезка ВС:

.

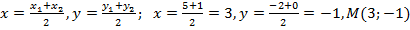Уравнение AM:

– уравнение медианы, проведенной из вершины А

2) Найдем уравнения СВ и CN; N(x; у), где

.

Тогда ВС: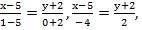

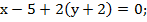
Ответ:

;

BC: x + 2y – 1 = 0;

CN: y = 0;

CA: x – y – 1 = 0;

BF: x + y – 3 = 0.