Рассмотрим случаи, когда интерполируемая функция y=f(x) задается в равноотстоящих узлах так, что 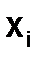 = x0 +ih, где h – шаг интерполяции, а i = 0, 1, …, n .
= x0 +ih, где h – шаг интерполяции, а i = 0, 1, …, n .
В этом случае для нахождения интерполяционного многочлена могут применяться формулы Ньютона, которые используют конечные разности.
Конечные разности
Конечной разностью первого порядка называется разность Dyi=yi+1-yi,где yi+1= f(xi+h) и yi = f(x i). Для функции, заданной таблично в (n+1) узлах,i = 0, 1, 2, …, n, конечные разности первого порядка могут быть вычислены в точках 0, 1, 2,…, n-1:
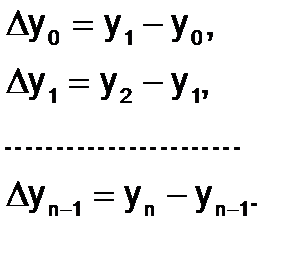
Используя конечные разности первого порядка, можно получить конечные разности второго порядка:
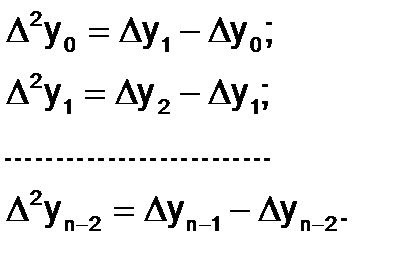
Отметим, что любые конечные разности можно вычислить через значения функции в узлах интерполяции, например:
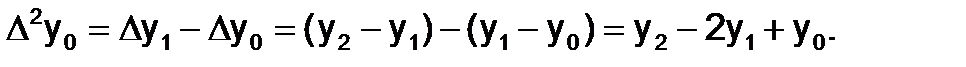 (1.3.3-1)
(1.3.3-1)
Для конечной разности k - го порядка в узле с номером iсправедлива формула,позволяющая вычислять конечные разности с помощью таблицы конечных разностей:
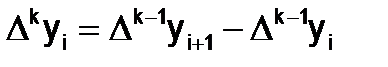 .
.
Следует отметить, что по величине конечных разностей можно сделать вывод о степени интерполяционного полинома, описывающего таблично заданную функцию. Если для таблицы с равноотстоящими узлами конечные разностиk-го порядка постоянны или соизмеримы с заданной погрешностью, то функцию можно представить многочленом k-й степени.
Рассмотрим, например, таблицу конечных разностей для многочлена y=x2-3x+2.
Таблица 1.3.3-1
| x | y | Dy | D2y | D3y |
| 1.0 | -0.16 | 0.08 | ||
| 1.2 | -0.16 | -0.08 | 0.08 | |
| 1.4 | -0.24 | 0.08 | ||
| 1.6 | -0.24 | 0.08 | ||
| 1.8 | -0.16 |
В данном примере конечные разности третьего порядка равны нулю, а все конечные разности второго порядка равны 0.08. Это говорит о том, что функцию, заданную таблично, можно представить многочленом второй степени.
Введя понятие конечных разностей, рассмотрим еще две формы записей интерполяционных полиномов.
 2017-12-14
2017-12-14 644
644







